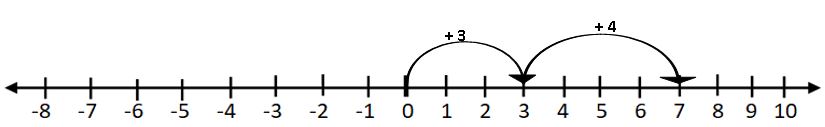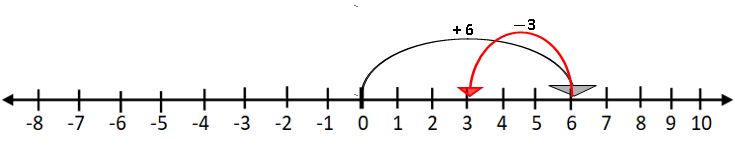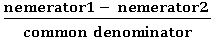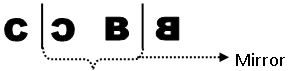- TS 6th Maths Concept
- TS 7th Maths Concept
- TS 8th Maths Concept
- TS 9th Maths Concept
- TS 10thMaths Concept
6th maths notes|| TS 6 th class Maths Concept
Studying maths in the 6th class successfully meaning that children take responsibility for their own learning and learn to apply the concepts to solve problems.
This note is designed by the ‘Basics in Maths’ team. These notes to do help students fall in love with mathematics and overcome fear.
1. KNOWING OUR NUMBERS
• Number: A number is a mathematical object used to count and measure.1,2,3…….etc.
Comparing numbers:
• We can compare the numbers by counting the digits in the numbers.
• Now Compare 5432 and 4678…
5432 is greater as the digits at the ten thousand place in 5432 is greater than that in 4678.
Order of numbers:
• Ascending Order: –
arrange the numbers from smallest to the greatest; this order is called Ascending order.
Ex:- 23, 44, 65, 79, 100
• Descending Order: –
arrange the numbers from greatest to the smallest, this order is called Ascending order.
Ex:- 100,79, 65, 33, 23
Formations of numbers
• Form the largest and smallest possible numbers using the digits 3, 2, 4, 1 without repetition
• Largest number formed by arranging the given digits in descending order _ 4321.
• Smallest number formed by arranging the given digits in ascending order _ 1234.
• Greatest two-digit number is 99.
• Greatest three-digit number is 999.
• Greatest four-digit number is 9999.
Place value
• Place value is the positional notation, which defines the position of a digit.
Ex:- 3458
8 is one place, 5 is tens place, 4 is hundreds place and 3 is thousands place.
Expanded form
• It refers to expand the numbers to see the value of each digit.
Ex :- 3458 = 3000 + 400 + 50 + 8
= 3×1000 + 4×100 + 5×10 + 8×1
• Note:-
1 hundred = 10 tens
1 thousand = 10 hundreds
1 lakh = 100 thousands = 1000 hundreds
Reading and Writing the numbers
Place value table for Indian system :
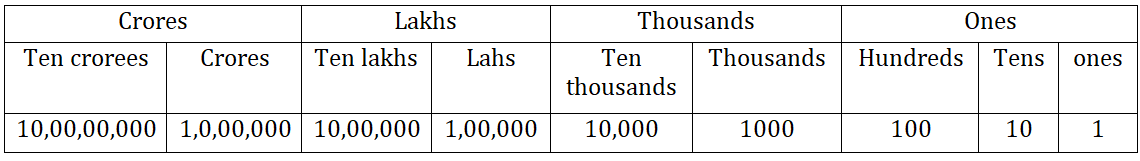
Example: Represents the number in 6,35,21,892 in place value table

Place value table for International system :
 Ex:- represents the number in 635,218,924 in place value table
Ex:- represents the number in 635,218,924 in place value table

Use of commas:
• Indian system of numeration:- in the Indian system of numeration we use ones, tens, hundreds, thousands, lakhs and crores. The first comma comes after three digits from the right, the second comma comes two digits latter and the third comma comes after another two digits.E
Ex:- “three crores thirty-five lakh seventeen thousand four hundred thirty” can be written as.3,35,17,430
• International system of numeration:- in the International system of numeration we use ones, tens, hundreds, thousands, millions and billions.
Ex:- “ six hundred thirty-five million two hundred eighteen thousand nine hundred twenty-four” can be written as 635,218,924.
Note:-10 millimetres = 1centimeter
100 centimetres = 1 meter
1000 meters = 1 kilometer
1000 milligrams = 1 gram
1000 grams = 1 kilo gram
2. WHOLE NUMBERS
Natural numbers: All the counting numbers starting from 1 are called Natural numbers.
1, 2, 3… Etc.
Successor and Predecessor: If we add 1 to any natural number, we get the next number, which is called the Successor. If we subtract 1 from any natural number, we get the previous number, which is called Predecessor.
Ex: – successor of 23 is 24 and predecessor of 32 is 31.
Note:- There is no predecessor of 1 in natural numbers.
Whole numbers: Whole numbers are the collection of natural numbers.
0, 1, 2, 3 …
Representation of whole number on the number line:
• Draw a line mark a point on it.
• Label it as ‘0’
• Mark as many points at equal distance to the right of 0.
• Label the points as 1, 2, 3, 4, … respectively.
• The distance between any two consecutive points is the unit distance.
Addition on the number line:
- The distance between 2 and 4 is 2 units, like as the distance between 2 and 6 is 4 units
- The number on the write is always greater than the number on the left
- The number on the left of any number is always smaller than that number
Addition of the whole number can represent on the number line
Ex:- 3 + 2 = 5
Start from three, we add 3 to 2. We make two jumps to the right of the number line as shown above. We reach at 5.
Subtraction on the number line:
Subtraction of the whole number can be represented on the number line

Ex :-5 – 3 = 2
Start from 5, we subtract 3 from 5. We make three jumps to the left of the number line shown as above. We reach at 2.
Multiplication on the number line:
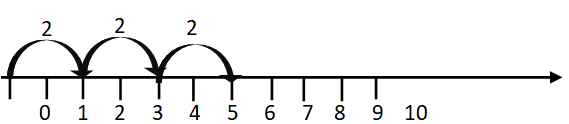 For multiplying 2 and 3, start from 0, make 2 jumps using 3 units at a time to the right, as you reach to 6. Thus, 2 × 3 =6.
For multiplying 2 and 3, start from 0, make 2 jumps using 3 units at a time to the right, as you reach to 6. Thus, 2 × 3 =6.
Properties of whole numbers
Closer property: Two whole numbers are said to be closed if their operation (+, -, ×,÷) is always closed.
Addition:-Whole numbers are closed under addition.
Ex: 3, 2 are whole numbers ⟹ 3 + 2 = 5 ( 5 is whole number)
Subtraction:- Whole numbers are not closed under subtraction as their difference not always a whole number.
Ex:- 2 – 3 = −1 ( −1 is not a whole number)
Multiplication:- Whole numbers are closed under multiplication.
Ex:- 3 × 2 = 6, 6 is a whole number.
Division:- Whole numbers are not closed under division, as their division is not always a whole number.
Ex:- 3 ÷ 2 is not a whole number.
Commutative property: Two whole numbers are said to be commutative if the result is the same when we change their position.
Addition:-Whole numbers are commutative under addition.
Ex: 3, 2 are whole numbers ⟹ 3 + 2 = 5 and 2 + 3 = 5 ( 3 + 2 = 2 + 3).
Subtraction:- Whole numbers are not commutative under subtraction.
Ex:- 2 – 3 = −1 and 3 – 2 = 1( 2 −3 ≠ 3 – 2 ).
Multiplication:- Whole numbers are commutative under multiplication.
Ex:- 3 × 2 = 6 and 2 ×3 = 6 (3 × 2 = 2 ×3)
Division:- Whole numbers are not commutative under division.
Ex:- 3 ÷ 2 ≠ 2 ÷ 3.
Associative property: For any three whole numbers a, b and c if (a ⨀ b)⨀ c = a ⨀ (b ⨀ c), then whole numbers are associative under operation ⨀. [ ⨀ = +, –, × and ÷ ].
Addition:-Whole numbers are associative under addition.
Ex: ( 3 + 2) + 5 = 10 and 3 + (2 + 5) = 10 ⟹ ( 3 + 2) + 5 = 3 + (2 + 5)
Subtraction:- Whole numbers are not associative under subtraction.
Ex:- : ( 3 − 2) − 5 = −4 and 3 − (2 − 5) = 6 ⟹ ( 3 + 2) + 5 ≠3 + (2 + 5)
Multiplication:- Whole numbers are associative under multiplication.
Ex:- (3 × 2) ×5 = 30 and 3 ×(2 × 5) = 30 ⟹ (3 × 2) ×5 = 3 ×(2 × 5)
Division:- Whole numbers are not associative under division.
Ex:- ( 3 ÷ 2) ÷ 5 ≠3 ÷ (2 ÷ 5).
Distributive property:
For any three whole numbers a, b and c, a×(b + c) = (a × b) +( a × c).
Note :Division by zero is not defining.
Identity under addition and multiplication:
2 +0 = 2, 5 + 0 = 5 and so on.
Thus, 0 is the additive identity.
2 ×1 = 2, 4 × 1 = 4 and so on.
Thus, 1 is a multiplicative identity.
Patterns:
- Every number can be arranged as a line. The number 2 is shown as

The number 3 as shown as![]()
- Some numbers can be shown as rectangles. 8 can be shown as
![]()
- Some numbers can be arranged as squares. 9 can be shown as

- Some numbers can be shown as triangles.
3 can be shown as  6 can be shown as
6 can be shown as

3. PLAYING WITH NUMBERS
Divisibility Rule:
The process of checking whether a number is divisible by a given number or not without actual division is called divisibility rule for that number.
Divisibility by 2:- a number is divisible by 2 if its once place is either 0, 2, 4, 6 or 8.
Ex:- 26 is divisible by 2. 35 not divisible by 2.
Divisibility by 3:- if the sum of the digits of a number is divisible by 3, then that number is divisible by 3.
Ex:- 231 → 2 + 3 +1 =6, 6 is divisible by 3
∴ 231 is divisible by 3
436 → 4 + 3 + 6 = 13, 13 is not divisible by 3
∴ 436 is not divisible by 3.
Divisibility by 4:- if the last two digits of a number is divisible by 4, then that number is divisible by 4.
Ex:- 436, 36 is divisible by 4 ∴ 436 is divisible by 4
623, 23 is not divisible by 4 ∴ 623 is not divisible by 4.
Divisibility by 5:- a number is divisible by 5, if its once place is either 0 or 5.
Ex:- 20, 25 are divisible by 5. 22, 46 are not divisible by 5.
Divisibility by 6:- a number is divisible by 6, if it is divisible by both 3 and 2.
Ex:- 242 is divisible by both 2 and 3 ∴ 242 is divisible by 6
232 is divisible by 3 but not 2 ∴ 232 is not divisible by 6
Divisibility by 8:- if the last three digits of a number is divisible by 8, then that number is divisible by 8.
Ex:- 4232, last three digits 232 are divisible by 8
∴ 4232 is divisible by 8.
Divisibility by 9:- if the sum of the digits of a number is divisible by 9, then that number is divisible by 9.
Ex:- 459, 4 + 5 + 9 = 18 → 18 is divisible by 9 ∴ 459 is divisible by 9
532, 5 + 3 + 2 = 10 → 10 is not divisible by 9 ∴ 532 is not divisible by 9.
Divisibility by 10:- a number is divisible by 10 if its once place is 0.
Ex:- 20 is divisible by 10. 22, 45 are not divisible by 10.
Divisibility by 11:- A number is divisible by 11 if the difference between the sum of the digits at odd places and the sum of the digits at even places is either 0 or 11.
Ex:- 6545
Sum of the digits at odd places = 5 + 5 = 10
Sum of the digits at even places = 4 + 6 = 10
Now difference is 10 – 10 = 0
∴ 6545 is divisible by 11.
Factors: a number which divides the other number exactly is called a factor of that number.
6 = 1×6
= 2×3 ⟹ factors of 6 are: 1, 2, 3 and 6
Note- 1)1 is a factor of every number.
2) Every number is a factor of itself.
3) Every factor is less than are equal to the given number.
4) Factors of a given number are countable.
Prime numbers: The numbers, which have only two factors 1, and itself are called prime numbers.
2, 3, 5, 7, …. Are prime numbers
Composite numbers: The number, which has more than two factors are called composite numbers.
4, 6,8,9….. are composite numbers.
- Note: – 1) 1 is neither prime nor composite
2) 2 is the smallest prime number
3) 4 is the smallest composite number.
Co – prime number: The number which has no common factor except 1 is called co-prime number.
Ex:- (2, 3), (4,5) ……
Twin – primes: If the difference of two prime numbers is 2, then those numbers are called twin prime numbers.
Ex:- (2,3), (3,5), (17,19)…..
Factorization: When a number is expressed as the product of its factors, we say that the number has been factorized. The process of finding the factors is called Factorisation.
Ex:- factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24
24 = 1 × 24 = 2 × 12 = 3 × 8 = 4 × 6
Prime factorisation: The process of finding the prime factors is called prime factorisation.
Ex:- 24 = 2 × 12
2 × 3 × 4
2 × 3 × 2 × 2
∴ Prime factorisation of 24 is 2 × 2 × 2 × 3.
Methods of prime factorization:
Division method:- Prime factorization of 12 using the division method,
fallow the procedure.
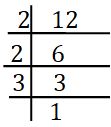
Start dividing by the least prime factor. Continue division till the resulting number to be divided is 1.
The prime factorization of 12 is 2 × 2 × 3.
Factor tree method:- To find the prime factorization of 24, using the factor tree method we proceed as follows:
- Express 24 as a product of two numbers.
 Factorise 4 and 6 further, since they are composite numbers.
Factorise 4 and 6 further, since they are composite numbers. - Continue till all factors are prime numbers.
- The prime factorization of 24 is 2 × 2 × 2 × 3.
Common factors: Common factors are those numbers, which are factors of all the given numbers.
Ex:- 12, 9
Factors of 12 are: 1, 2, 3, 4, 6 and 12
Factors of 9 are: 1, 3 and 9
∴ Common factors of 12, 9 are 1,3
Highest Common Factor (H.C.F):- The highest common factor of two or more numbers is the highest of their common factors. It is also called ad Greatest Common Divisor(G.C.D).
Ex:- H.C.F of 12, 9
Factors of 12 = 1, 2, 3,4, 6, 12
Factors of 9 = 1, 3, 9
Common factors of 12, 9 = 1,3
Highest common factor is 3
∴ H.C.F of 12, 9 is 3
Method of finding HCF:
Prime factorization method:
The HCF of 9 , 12 can be found by the prime factorization method as follows.
9 = 3 × 3
12 =3 × 2× 2 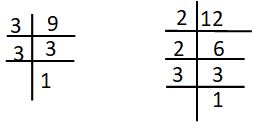
The common factor of 12, 9 is 3
∴ H.C.F of 12, 9 is 3
Continue division method:
Euclid invented this method. Divide the larger number by smaller and then divide the previous divisor by the remainder until the remainder zero. The last divisor is the HCF of given numbers.
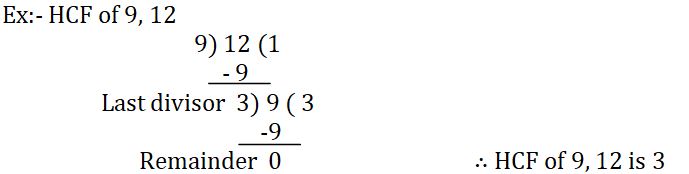
Common multiple multiples of 3 are 3, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39,42…
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52….
Common multiples of 3 and 4 are 12, 24, 36….
Least common multiple (LCM):- The least common multiple of two or more given numbers is the lowest of their common multiple.
Ex:- LCM of 3 and 4
Multiples of 3 = 3, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39,42…
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52….
Common multiples of 3 and 4 = 12, 24, 36….
∴ LCM of 3, 4 is 12.
Methods of finding LCM:
1. Prime factorization method:- the LCM of 6, 15 by using prime factorization method is as follows:
i) Express each number as the product of prime factors
Prime factors of 6 = 2 × 3
Prime factors of 15 = 5× 3
ii) Take the common factors both: 3
iii) Take the extra factors of both 6 and 15 i.e., 2 and 5
iv) The product of all common factors of two numbers and extra common factors of both finds LCM.
∴ LCM of 6 and 15 = (3) × 2 × 5 = 30.
2. Division method:- To find LCM of 6 and 15:
i. Arrange the given numbers in a row.
ii. Then divide the least prime number, which divides at least two of the given numbers, and carry forward the numbers, which are not divisible by that number if any.
iii.Repeat the process till no numbers have a common factor other than 1.
iv. LCM is the product of the divisors and the remaining numbers.
Ex:-
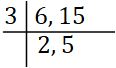
∴ LCM of 6, 15 = 3 × 2 × 5 = 30.
Note:- the product of LCM and HCF of given numbers = the product of given numbers.
Ex:- 6 × 15 = 30 × 3 = 90.
4.BASIC GEOMETRICAL IDEAS
The term ‘geometry’ is derived from the Greek word ‘geometron’.
Geo means Earth and metron means measurement.
Point: Point is a location or position on the surface of the plane. It is denoted by capital letters of the English alphabet.
Line: It is made up of infinitely many points with infinity length.
Ray: Ray is a part of a line. It begins at a point and goes on endlessly n a specific direction.
It is denoted by ![]()
Line segment: It is a part of the line with the finite length. ![]()
Intersecting lines: If two lines are meeting at the same point, then those lines are called intersecting lines. That pint is called the point of intersection.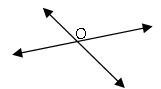
Parallel lines: The lines, which are never meet at any point, are called parallel lines. 
Curve: Anything, which is not straight, is called Curve.
Simple curve: – A curve that does not cross itself.
Open curve: – A curve in which its endpoints do not meet.![]()
Closed curve: – A curve that has no endpoint is called a closed curve.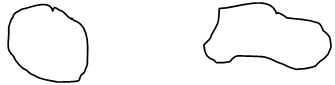
∗ A closed curve has three parts
The Interior of the curve: – It refers to the inside area of the curve. (B)
The exterior of the curve: – It refers to the outside area of the curve. (A)
On the curve: – It refers to the inside area of the curve. (C)
Polygon: – polygon is a simple closed figure made by line segments.
Angle: the figure formed by two rays having a common end is called an angle.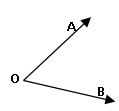
Here two rays OA, OB are arms of the angle
O is the Vertex. It is denoted by ∠AOB or ∠ BOA.
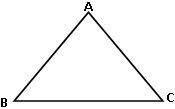
Triangle: A simple closed figure formed by the three line segments is a triangle. The line segments are called sides of the triangle.
- AB, BC and AC are sides of a triangle.
- A, Band C are vertices of a triangle.
- ∠ABC, ∠BAC and ∠ACB are angles of the triangle.
- This triangle is denoted by ∆ABC.
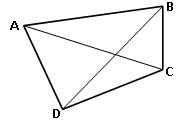
Quadrilateral: A simple closed figure formed by the four-line segments is a Quadrilateral.
- A, B, C and D are the vertices of the quadrilateral.
- ∠A, ∠B, ∠C and ∠D are the angles of quadrilateral.
- AB, DC and BC, AD are opposite sides of the quadrilateral.
- AB, BC; AD, DC; DC, BC and AD, AB are adjacent sides( the sides which have common vertex are called adjacent sides)
- A, C and B, D are opposite vertices and also opposite angles.
- AC and BD diagonals of a rectangle (A line segment joining opposite vertices is called diagonal).
Circle: The set of points that are at a constant distance from a fixed point is called a circle. The fixed point is called the centre of the circle and the constant distance is called the radius of the circle.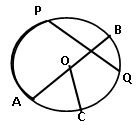
- O is the center of the circle.
- OA, OB, and OC radii of the circle
- AB is the diameter of the circle.
- PQ is a chord.
Circumference of the circle: – the length of the boundary of the circle is called the circumference of the circle.
Arc: – The part of the circumference is called Arc. From the above fig. is an arc.APisarc.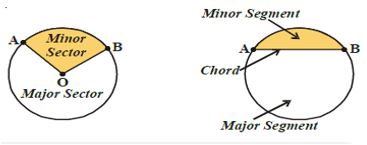
Sector: – Region enclosed by an arc and two radii is called a sector.
Segment: – The region enclosed by arc and chord is called a segment of the circle.
5. MEASURES OF LINES AND ANGLES
Measure of line segment:
- A line segment is a part of the line with two endpoints.
- This makes it possible to measure a line segment.
- This measure of each line segment is its ‘length’.
- We use length to compare line segments.
- We can compare the length of two line segments by: (i) simple observation (ii) tracing on a paper and (iii) using instruments.
Simple observation: – We can tell which line segment is greater than other just by observing the two-line
Here we can clearly say that CD > AB but sometimes it is difficult to tell which one is greater.
Tracing on a paper: – In this method we have to trace one line on paper then put the traced line segment on the other line to check which one is greater.
But this is a difficult method because every time to measure the different size of line segments we have to make a separate line segment.
Comparing by instruments: – To compare any two-line segments accurately, we use ruler(scale) and divider.
∗ We can use a ruler to measure the length of a line segment.
Put the zero mark at point A and then move toward l to measure the length of the line segment, but it may have some errors based on the thickness of the ruler.
∗ This could be made accurate by using a Divider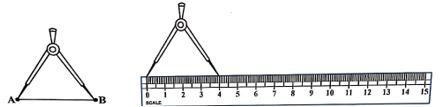
- Put the one end of the divider on point A and open it to put another end on point B.
- Now pick up the divider without disturbing the opening and place it on the ruler so that one end lies on “0”.
- Read the marking on the other end and we can compare the two line.
Measure of an angle: Angle is formed two rays or two-line segments.
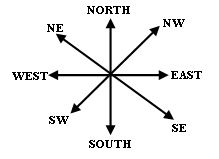
- We can understand the concept of right and straight angles by directions.

- There are four directions-North, South, East and West.
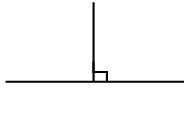
- When we move from North to East then it forms an angle of 90°, which is called Right Angle.
- When we move from North to South then it forms an angle of 180°, which is called Straight Angle.
- When we move four right angles in the same direction then we reach to the same position again i.e. if we make a clockwise turn from North to reach to North again then it forms an angle of 360°, which is called a Complete Angle. This is called one revolution.
∗ In a clock, there are two hands i.e. minute hand and hour hand, which moves clockwise in every minute. When the clock hand moves from one position to another then turns through an angle.
- When a hand starts from 12 and reaches to 12 again then it is said to be completed a

- s were the ray moves in the opposite direction of the hands of a clock are called anti – clockwise angles. These are denoted by positive measure.
- Angles were the ray moves in the direction of the hands of a clock are called clockwise angles. These are denoted by negative measure.
- By observing an angle we can only get the type of angle but to compare it properly we need to measure it.
- An angle is measured in the “degree”. One complete revolution is divided into 360 equal parts so each part is one degree. We write it as 360° and read as “three hundred sixty degrees”.
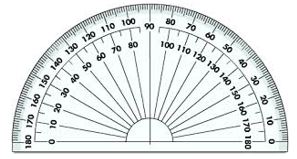
- We can measure the angle using a ready to use device called Protractor.
- It has a curved edge, which is divided into 180 equal parts. It starts from 0° to 180° from right to left and vice versa.
∗To measure an angle 72° using protractor-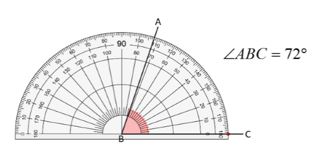
- Place the protractor on the angle in such a way that the midpoint of protractor comes on the vertex B of the angle.
- Adjust it so that line BC comes on the straight line of the protractor.
- Read the scale, which starts from 0° coinciding with the line BC.
- The point where the line AB comes on the protractor is the degree measure of the angle.
Hence, ∠ABC = 72°.
Types of angles:
Type of angle | Measure |
Zero angle | 0° |
Right angle | 90° |
Straight angle | 180° |
Complete angle | 360° |
Acute angle | Between 0° to 90° |
Obtuse angle | Between 90° to 180° |
Reflex angle | Between 180° to 360° |
If two lines intersect with each other and form an angle of 90° then they must be perpendicular to
6.INTEGERS
There several situations in our daily life, where we use these numbers to represent loss or profit; past or future; low or high temperature. The numbers on the left side of zero are called negative numbers.
Integers: The numbers which are positive, zero and negative numbers together are called as integers and they re denoted by I or Z.
Z = {…, -3, -2, -1, 0, 1, 2, 3…}.
Representation of integers on a number line: –
- The numbers which are on the right side of zero are positive numbers and which are on the left side of zero are negative numbers.
- 0 is neither positive nor negative.
- On a number line, the number increases as we move to right and decrease as we move to the left.
∴ -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 so on.
- Note: – 1. Any positive integer is always greater than any negative integer
- Zero is less than every positive integer.
- Zero is greater than every negative integer.
- Zero doesn’t come in any of the negative and positive integers.
Addition and subtraction of integers:
1.If two integers have same sign, then add the integers and put that sign before the result.
Ex: – 3 + 2 =5, −3 – 2 = −5.
2.If two integers have different sign, then subtract smaller one from bigger and put the bigger one sign before the result.
Ex: – 3 − 2 =1, −3 + 2 = −1, −10 + 5 = −5.
Addition of integers on a number line:
Add 3 and 4
- On the number line, we first move three steps to the right of 0 to reach 3, then we move 4 steps to the right of 3 and to reach 7
∴ 3 + 4 = 7
Add −3 and −4
- On the number line, we first move three steps to the left of 0 to reach −3, then we move 4 steps to the left of −3 and to reach −7.
∴ − 3 − 4 = −7
∗ Any two distinct numbers that give zero when added to each other are additive inverse each other.
Subtraction of integers on a number line:
Subtract 3 from 6
- On the number line, we first move 6 steps to the right of 0 to reach 6, then we move 3 steps to the left of 6 and to reach 3.
∴ 6 − 3 = 3.
Subtract −3 from 6
On the number line, we first move 6 steps to the right of 0 to reach 6. For – 3 we have to move left but for – ( −3) we move in the opposite direction. Thus, we move 3 steps to the left of 6 and to reach 9.
∴ 6 – (−3) = 9.
• Subtraction of integers is the same as the addition of their additive inverse.
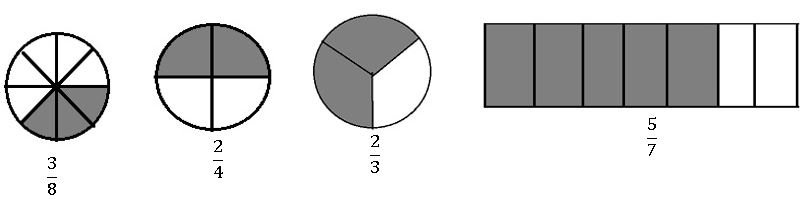
7. FRACTIONS AND DECIMALS
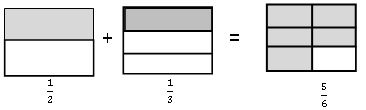
A fraction means a part of a group of a whole.
The ‘whole’ here could be an object or the group of objects. But all the parts of the whole must be equal. The ‘whole’ here could be an object or the group of objects. However, all the parts of the whole must be equal.
• Fig(i) is the whole. The complete circle.
• In Fig (ii), we divide the circle into two equal parts, then the shaded portion is the half ie., ![]() of the circle.
of the circle.
• In Fig (iii), we divide the circle into three equal parts, then the shaded portion is the one third of the circle i.e.,![]() of the circle.
of the circle.
• In Fig (iv), we divide the circle into four equal parts, then the shaded portion is the one fourth of the circle i.e.,![]() of the circle.
of the circle.
The numerator and the denominator:
The upper part of the fraction is called ‘numerator’. It tells the no. of parts we have.
The lower part of the fraction is called ‘denominator’. It tells the total parts in whole.
Representing fractions pictorially:
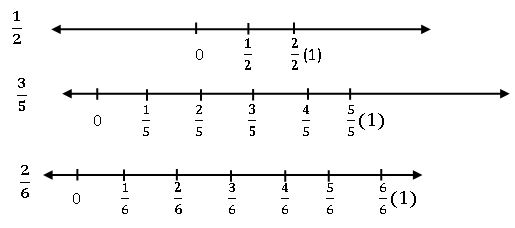
Representing fractions on a number line:
Proper fractions: In a fraction if the numerator is less than denominator then, then it is called proper fraction. If we represent a proper fraction on a number line then it is always lies between 0 and 1.
Improper fractions: In a fraction if the numerator is greater than denominator then, then it is called improper fraction.
Mixed fractions: – The fraction made by the combination of whole number and a part is called mixed fraction.
Note: Only improper fractions can be represented as mixed fractions.
A mixed fraction is in the form of ![]()
We can convert it into improper fraction by ![]()
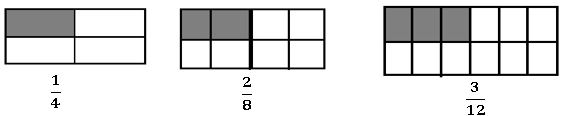
Equivalent fractions: – Equivalent fractions those fractions which represent the same part of whole.
- Equivalent fractions are arising when we multiply both the numerator and denominator by the same number.
- Equivalent fraction of
 are
are  and so on
and so on
Standard form of a fraction (simplest or lowest form):- A fraction is said to be in standard form if both the numerator and denominator of that fraction have no common factor except 1.
Like and Unlike fractions: The fractional numbers that have the same denominators are called fractional numbers and have not the same denominator are called unlike fractions.
Ex: – ![]() are like fractions and
are like fractions and ![]() are un like fractions.
are un like fractions.
Comparing fractions:
Like fractions: – We have to compare the like fractions with the numerator only, because the like fractions have same denominator. The fraction with greater numerator is greater and the fraction with smaller numerator is smaller.
Unlike fractions: –
With same numerator: For comparing unlike fractions, we have to compare denominators when the numerator is same. The fraction with greater denominator is smaller and the fraction with smaller denominator is smaller.
Note: – To find the equivalent fractions of both the fractions with the same denominator, we have to take the LCM of their denominators.
Ascending order and Descending order: –
When we write numbers in a form that they increase from the left to right then they are in the Ascending order. When we write numbers in a form that they decrease from the left to right then they are in the Descending order.
Ex: – For fractions: 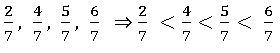 are in ascending order and
are in ascending order and ![]() are in descending order.
are in descending order.
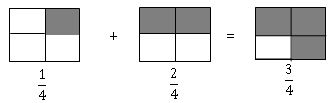
Addition of fractions:
Like fractions: –
Un like fractions: – For adding unlike fractions, first we have to find the equivalent fraction of given fractions and then add them as like fractions.
Subtraction of fractions
Like fractions: –
Un like fractions: – First we have to find the equivalent fraction of given fractions and then subtract them as like fractions.
Decimal fractions:
A fraction where the denominator is a power of ten is called decimal fraction. We can write decimal fraction with a decimal point (.). it makes easier to do addition, subtraction and multiplication on fractions.
8. DATA HANDLING
Data: collection of information in the form of numbers or words is called data.
Recording data: Recording of data depends on the requirement of the data. We can record data in different ways.
Organization of data: –
- Data is difficult to read.
- We have to organize it.
- Data can be organized in a tabular form.
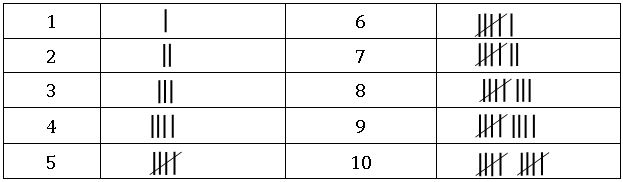
- Data is represented in tabular form using frequency distribution and the tally marks.
- Frequency tells the no. of times the observations is happened.
- Tally marks show the frequency of the data.
∗ Example for representing tally marks:
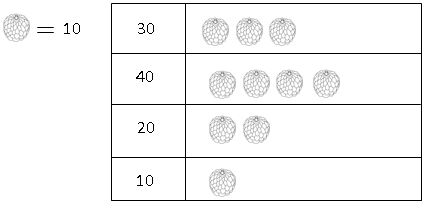
Pictograph:
If the data is represented by the picture of objects instead if numbers, then it is called pictograph. Pictures make it is easy to understand the data and answer the questions to related it by observing the pictures.
Example for representing data by pictograph
- Drawing a pictograph is difficult to draw some difficult pictures.
- For understanding every one, e must use proper symbols.
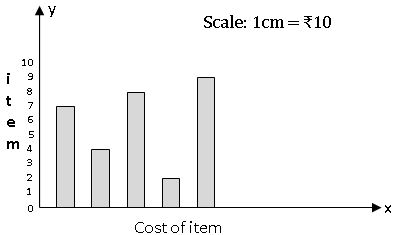
Bar graph:
• Bar graphs are used to represent the independent observations with frequencies.
• In a bar graph, bars of uniform width are drawn horizontally or vertically with equal spacing between them.
Construction of bar graph: –
Steps to construction: –
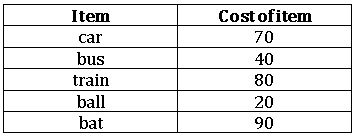
1.Draw two perpendicular lines one horizontal (x – axis) and one vertical (y – axis).
2.Along the x- axis mark ‘items’ and along the x – axis mark ‘cost of items’.
3.Select a suitable scale 1cm = 10(rupees).
4.Calculate the heights of the bars by dividing the frequencies with the scale
70 ÷ 10 = 7, 40 ÷ 10 = 4 and so on.
5.Draw rectangular vertical bars of same width on the x- axis with heights calculated above.
9. INTRODUCTION TO ALGEBRA
Algebra is the use of letters or symbols to represent number. It helps us to study about un known quantities.
Patterns:
To make a triangle, 3 matchsticks are used 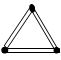
For making 2 triangles we have six matchsticks 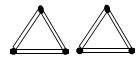
For making 3 triangles we have nine matchsticks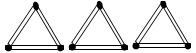
- of matchsticks required for making 1 triangle = 3 = 3 × 1
- of matchsticks required for making 2 triangles = 6 = 3 × 2
- of matchsticks required for making 3 triangles = 9 = 3 × 3
Thus the no. of matchsticks for making ‘n’ triangles = 3 × n = 3n.
Variable: Variable is a unknown quantity that may change. It is a dependent term.
In the above pattern, the rule is 3n, here ‘n’ is the variable.
- We can use lower case alphabets are used as variable.
- Numbers cannot use as variables, since they have fixed value.
- Variables help us to solve other problems also.
- Variables can take different values; they have no fixed value.
- Mathematical operations addition, subtraction, multiplication and division can be done on the variables.
Use of variables:
⋇ perimeter of a polygon is the sum of the lengths of all its sides.
Perimeter square = 4s, s is the variable
Perimeter of rectangle = 2 (l + b); l, b are variables.
⋇ To find the nth term from the given pattern: 3, 6, 9…
Number | 3 | 6 | 9 | 12 | 15 | … |
Pattern | 3×1 | 3×2 | 3×3 | 3×4 | 3×5 | … |
From the table we observe that, the first number is 3×1, the second number is 3×2, the third number is 3×3 and so on.
∴ the nth term of pattern 3, 6, 9, 12, = 3n, here n is variable.
Simple equation: simple equation is a condition to be satisfied by the variables. Equation has equality sign between its two sides.
Ex: 5m = 10, 2x + 1 = 0 etc.
L.H.S and R.H.S of an equation:
The expression which is at the left of equal sign of an equation is called Left Hand Side (L.H.S)
The expression which is at the right side of equal sign of an equation is called Right Hand Side (R.H.S)
Ex: 4y = 20
L.H.S = 4y and R.H.S = 20
Solution of an equation (Root of the equation):
Solution or Root of an equation is the values of variable for which L.H.S and R.H.S are equal.
Ex: 3x = 15
If x = 5; LHS = 3×5 = 15
RHS = 15
∴ solution of above equation is 5
Trial and error method:
By using this method, we get the solution of given equation.
Ex: solve 2n = 10
Substituting value of n | Value of L. H. S | Value of R. H. S | Whether LHS and RHS are equal |
1 | 2×1 = 2 | 10 | Not equal |
2 | 2×2 = 4 | 10 | Not equal |
3 | 2×3 = 6 | 10 | Not equal |
4 | 2×4 = 8 | 10 | Not equal |
5 | 2×5 = 10 | 10 | Equal |
When n = 5, LHS = RHS ∴ solution of equation is 5.
10. PERIMETER & AREA
Perimeter: Perimeter is the distance covered along the boundary forming a closed figure when you go around the figure once.
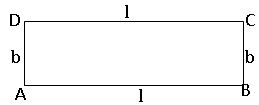
Perimeter of a Rectangle:
Length of the rectangle = l, breadth = b
Perimeter of rectangle = sum of the lengths of its sides.
= l + l +b + b
P = 2 (l + b) units.
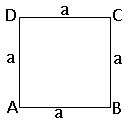
Perimeter of a Square:
Length of the side of a square = a
Perimeter of rectangle = sum of the lengths of its sides.
= a + a + a + a
= 4a units.
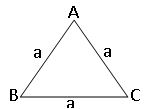
Perimeter of an Equilateral Triangle:
Length of each side = a
Perimeter of rectangle = sum of the lengths of its sides.
= a + a + a
= 3a units.
Polygon: A polygon is a simple closed figure bounded by line segments.
Regular polygon: A polygon which has equal side and equal angles, is called Regular polygon.
The perimeter of regular polygon of ‘n’ sides whose length ‘a’ = na.
Area: The amount of surface enclosed by a closed figure is called its area.
Area of a Rectangle:
Length of the rectangle = l, breadth = b
Area of the Rectangle = l × b square units.
Area of a Square:
Length of the side of a square = a
Area of a Square = a × a = a2 square units.
Note: The area of the square is more than the area of any other rectangle having the same perimeter.
PDF Files || Inter Maths 1A &1B || (New) |
11. RATIO AND PROPORTION
Ratio: Ratio is the comparison of two quantities of same kind.
The ratio of two quantities a and b is written as a: b and read as ‘a is to b’.
‘a’ is called first term or antecedent and ‘b’ is called second term or consequent.
Simplest form of ratio:
If a ratio is written in terms of whole numbers with no common factors other than 1, then the ratio is said to be in the ‘simplest form’ or in the ‘lowest terms’.
Ex: the simplest form of 5 : 15 is 1 : 3.
Division of a given quantity in a given ratio:
Let us suppose that, if a quantity ‘c’ divided into two parts in the ratio a: b, then
Total parts = a + b
Ex: Divide 1200 in the ratio 2 : 3
Ans: Total parts = 2 + 3 = 5
Proportion:
Equalities of ratios is called proportion.
If a : b = c : d, then a ,b ,c and dare in proportion. This is represented as a : b ∷ c : d.
If a, b, c and d are in proportion, then ad = bc.
Unitary method:
In this method, first we find the value of one unit and then the value of the required number of units.
Ex: If the cost of 5 pens is ₹ 20, then find the cost of 12 pens.
Sol: Given that cost of 5 pens = ₹20
Cost of one pen = 20 ÷ 5= 4
Cost of 12 pens = 4 × 12 = 48
∴ cost of 12 pens = ₹ 48.
12. SYMMETRY
Symmetry:
The word symmetry comes from Greek word. It means ‘to measure together’.
Symmetry is the mirror image of an object.
Symmetry means that one object becomes exactly like another when we move it in some way: turn, flip or slide.
Ex:
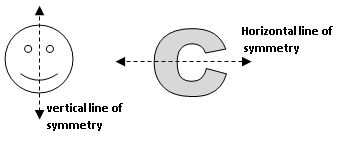
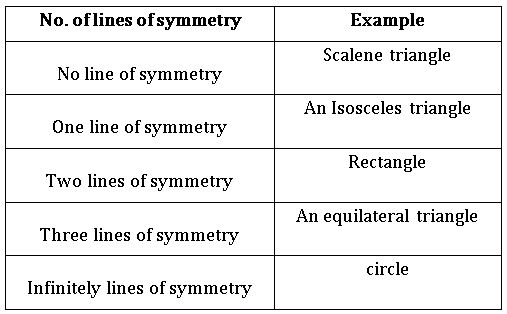
Line of symmetry:
A line along which you can fold a figure so that two parts of it coincide exactly is called a ‘line of symmetry’.
Line of symmetry can be horizontal, vertical or diagonal.
Ex:
 The English alphabet which have
The English alphabet which have
- Vertical line of symmetry: A, H, I, M, O, U, V, W and X
- Horizontal line of symmetry: B, C, D, E, H, I, K, O and X
- No line of symmetry: D, G, J, L, N, P, Q, R, S, Y AND Z.
13. PRACTICAL GEOMETRY
The following instruments from a geometry box are used to construct figures:
1.A Ruler (Scale)
2.The compasses
3.The divider
4.Protractor
∗ The ruler is used to measure lines.
∗ The compasses is used for constructing.
∗ The protractor is used for measuring angles.
∗ Divider is used to make equal line segments or mark point on a line.
Construction of a line segment of a given length:
We can construct a line segment in two ways: 1) By using Ruler 2) By using the Compasses
1.By using Ruler: –
Let us suppose we want to draw a line segment AB of length 3.5 cm
Steps of construction: –
Step-1: Place the ruler on a paper and hold it firmly.
Step-2: Mark a point with sharp edged pencil against ‘0cm’ mark of the ruler.
Step-3: Name the point as A. Mark another point against 5 small divisions just after the 3cm mark. Name this point as B
Step-4: Join A and B along the edge of the ruler. AB is the required line segment of length 3.5cm.
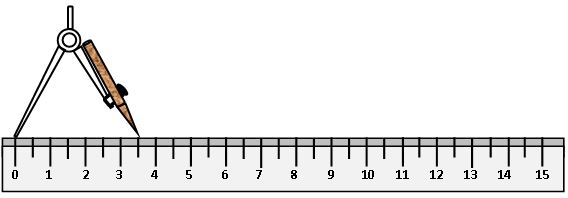
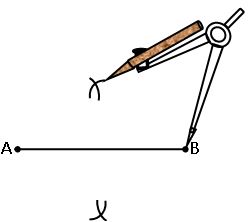
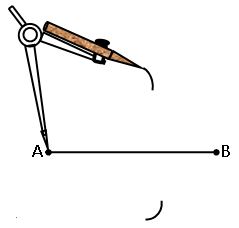
1.By using the Compasses: –
Let us suppose we want to draw a line segment AB of length 3.5 cm
Steps of construction:
Step-1: draw a line l. Mark a point on the line l.
![]()
Step-2: place the metal pointer of the compasses on the zero mark of the ruler. open the compasses so that the pencil point touches the 3.5cm mark on the ruler.
Step-4: on the line l, we got the line segment AB of length 3.5cm.
![]()
Step-3: place the pointer on A on the line l and draw arc to cut the line. Mark the point where the arc cuts the line as B.
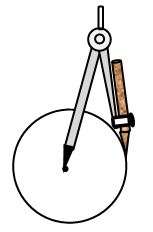
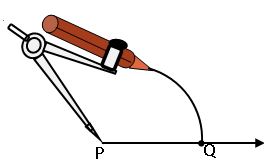
Construction of a circle:
Let us suppose we want to draw a circle of radius 3 cm
Steps of construction: –
Step-1: Open the compasses for radius 3 cm
Step-2: Mark a point with sharp edged pencil. This is the centre.
Step-3: Place the pointer of the compasses firmly at the centre.
Step-4: Without moving its metal point, slowly rotate the pencil and till it come back to the straight point.
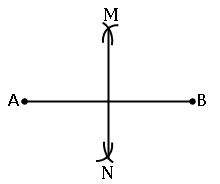
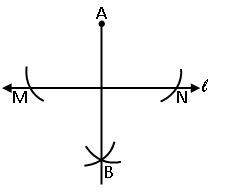
Construction of perpendicular bisector a line segment:
Steps of construction: –
Step-1: Draw a line segment AB.![]()
Step-2: Set the compasses as radius more than half of the length of line segment AB.
 Step-3: With A as centre, draw arcs below and above the line segment
Step-3: With A as centre, draw arcs below and above the line segment
Step-4: With the same radius and B as the center draw two arcs above and below the line segment to cut the previous arcs. Name the intersecting points of arcs as M and N.
Step-5: Join the points M and N. Then, the line MN is the required perpendicular bisector of the line segment AB.
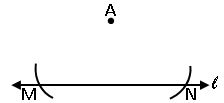
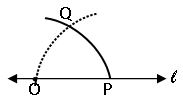
Construction of perpendicular to a line, through a point which is not on it:
Steps of construction: –
Step-1: Draw a line l and a point A not on it 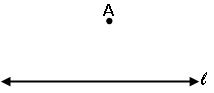
Step-2: With A as center draw an arc that intersects the given line at two points M and N.
Step-3: Using the same radius and with M and N as centres construct two arcs that intersect at a point B on the other side of the line.
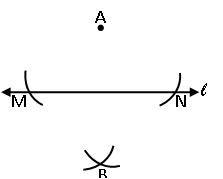 Step-4: Join A and B. AB is the perpendicular of the given line l.
Step-4: Join A and B. AB is the perpendicular of the given line l.
 Construction of Angles using Protractor:
Construction of Angles using Protractor:
Let us suppose we want to construct ∠ABC = 500
Steps of construction: –
Step-1: Draw a ray BC of any length.
Step-2: Place the center point of the protractor at B and the line aligned with the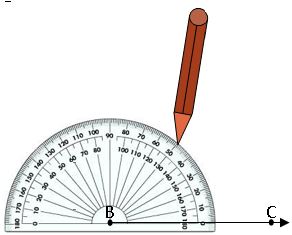
Step-3: Mark a point A at 500
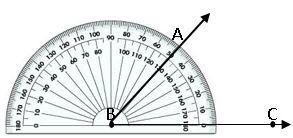 Step-4: join AB. ∠ABC is the required angle.
Step-4: join AB. ∠ABC is the required angle.
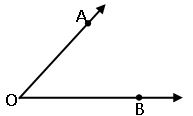
Constructing a copy an of Angle of unknown measure:
Let ∠A is given, measure is not known
Steps of construction: –
Step-1: Draw a line  and choose a point A on it.
and choose a point A on it.
Step-2: Now place the compasses at A and draw an arc to cut the rats AC and AB.

Step-3: Use the same compasses setting to draw an arc with P as centre, cutting l at Q.
Step-4: Set your compasses with BC as the radius.
Step-5: Place the compasses pointer at Q and draw an arc to cut the existing arc at R.
Step-6: Join PR. It has the same measure as ∠BAC.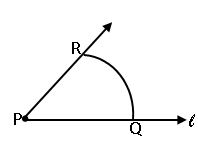
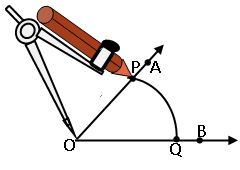
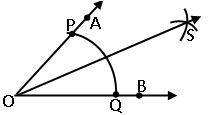
Construction to bisect a given angle:
Let an angle say ∠AOB be given
Steps of construction: – 
Step-1: With O as the centre and ray convenient radius, draw an arc PQ cutting OA and OB at P and Q respectively.
Step-2: With P as the centre and any radius slightly more than half of the length of PQ, draw an arc in the interior of the given angle.
Step-3: With Q as the centre and without alternating radius draw another arc in the interior of ∠AOB.
Let two arcs intersects at S
Step-4: Draw ray , then![]() is the bisector of ∠AOB
is the bisector of ∠AOB
Observe ∠AOS = ∠SOB
CONSTRUCTION ANGLES OF SPERCIAL MEASURES:
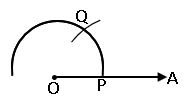
Construction of 600 angle: –
Steps of construction: –
Step-1: Draw a line l and mark a point O on it. ![]()
Step-2: Place the pointer at O and draw an arc of convenient radius which cuts the line at P (say).
Step-3: With the centre P and the same radius as in the step-2. Now draw an arc that passes through O.
Step-4: Let the two arcs intersects at Q. Join OQ. We get ∠POQ = 600.
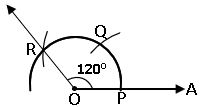
Construction of 1200 angle: –
Steps of construction: –
Step-2: Place the pointer of the compasses at O. With O as the centre and any convenient radius draw an arc cutting OA at P.
Step-3: With P as the centre and the same radius as in the step-2 draw an arc which cuts the first arc at Q.
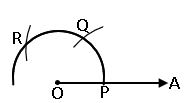 Step-4: With Q as the centre and the same radius as in the step-2 draw an arc which cuts the first arc at R.
Step-4: With Q as the centre and the same radius as in the step-2 draw an arc which cuts the first arc at R.
Step-5: Join OR. Then ∠POR = 1200.
14. UNDERSTANDING 3D AND 2D SHAPES
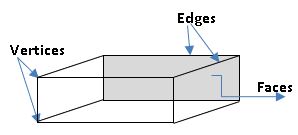
Cuboid:3D- shapes or Solids:
The object which have a length, breadth and height (or depth) are called ‘three dimensional’ or ‘3D- shapes’ or ‘Solids’.
Objects like match boxes, and erasers are the examples for cuboid
A cuboid has 6- Faces, 8- Vertices and 12 – Edges
A dice is an Example of a cube.
A cube has 6- Faces, 8- Vertices and 12 – Edges
Objects like wooden logs, a pieces of pipe are examples of cylinder
the top and base of the cylinder are circular in shape.
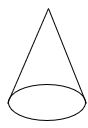
Cone:
A joker cap is an example for a cone
the base of the cone is a circle.
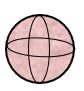
Sphere:
Balls and laddoos are examples of spheres.
If the base of a prism is the triangle, then it is called a triangular prism.
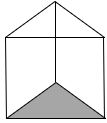
Pyramid:
A pyramid is a solid shape with a base and point vertex.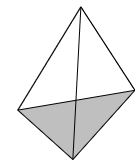
If a pyramid has a triangular base, then it is called a triangular pyramid![]()
If a pyramid has a square base, then it is called a square pyramid.
Polygon: A polygon is a closed figure made with line segments.
Regular Polygon: A polygon with all equal sides and all equal angles is called a regular polygon.
- TS 6th Maths Concept
- TS 7th Maths Concept
- TS 8th Maths Concept
- TS 9th Maths Concept
- TS 10th Maths Concept
Visit My Youtube Channel: Click on the below logo


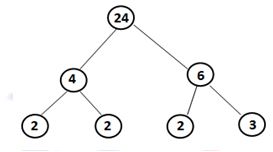 Factorise 4 and 6 further, since they are composite numbers.
Factorise 4 and 6 further, since they are composite numbers.