12 th Class Maths Concept
12 th Class Maths: This note is designed by ‘Basics in Maths’ team. These notes to do help the CBSE 12th class Maths students fall in love with mathematics and overcome their fear.
These notes cover all the topics covered in the CBSE 12th class Maths syllabus and include plenty of formulae and concept to help you solve all the types of 12thMath problems asked in the CBSE board and entrance examinations.
12 th Class Maths
1. RELATIONS AND FUNCTIONS
Ordered pair: Two elements a and b listed in a specific order form. An ordered pair denoted by (a, b).
Cartesian product: Let A and B are two non- empty sets. The Cartesian product of A and B is denoted by A × B and is defined as set of all ordered pairs (a, b) where a ϵ A and b ϵ B.
Relation: Let A and B are two non-empty sets the relation R from A to B is subset of A×B.
⇒ R: A→B is a relation if R⊂ A × B
Types of relations:
Empty relation: – A relation in a set A is said to be empty relation, if no element of A is related to any element of A.
R = ∅ ⊂ A × A
Universal Relation: – A relation in a set A is said to be universal relation, if each element of A is related to every element of A
R = A × A
Both empty relation and universal relation are sometimes called trivial relations.
Reflexive relation: A relation R in a set A is said to be reflexive,
if ∀a ∈ A ⇒ (a, a) ∈ R.
Symmetric relation: A relation R in a set A is said to be symmetric,
if ∀a, b ∈ A ⇒, (a, b) ∈ R ⇒ (b, a) ∈ R.
Anti-Symmetric relation: A relation R in a set A is said to be Anti-symmetric,
if ∀a, b ∈ A; (a, b) ∈ R (b, a) ∈ R ⇒ a = b.
Transitive relation: A relation R in a set A is said to be Transitive,
if ∀a, b, c∈ A; (a, b) ∈ R (b, c) ∈ R ⇒ a = c.
Equivalence relation: A relation R in a set A is said to equivalence, if it is reflexive, symmetric and transitive.
Function: A relation f: X → Y is said to be a function if ∀ xϵ X there exists a unique element y in Y such that (x, y) ϵ f.
(Or)
A relation f: A → B is said to be a function if (i) x ϵ X ⇒ f(x) ϵ Y
(ii) x1, x2 ϵ X, x1 = x2 in X ⇒ f(x1) = f(x2) in Y.
TYPES OF FUNCTIONS
One– one Function (Injective): – A function f: X→ Y is said to be one-one function or injective if different elements in X have different images in Y.
(Or)
A function f: X→ Y is said to be one-one function if f(x1) = f(x2) in Y ⇒x1 = x2 in X.
On to Function (Surjection): – A function f: X→ Y is said to be onto function or surjection if for each yϵ Y there exists x ϵ X such that f(x) = y.
Bijection: – A function f: X→ Y is said to be Bijection if it is both ‘one-one’ and ‘onto’.
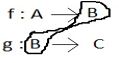
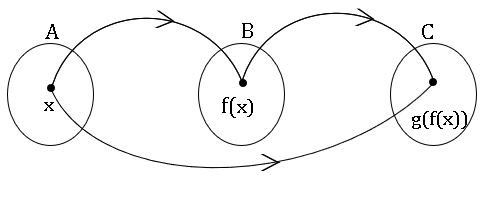
Composite function: If f: A→B, g: B→C are two functions then the composite relation gof is a function from A to C.
gof: A→C is a composite function and is defined by gof(x) = g(f(x)).