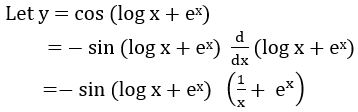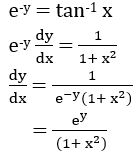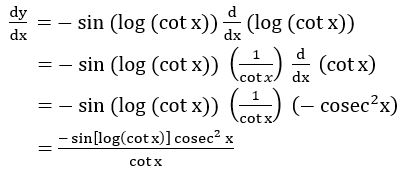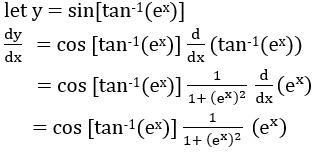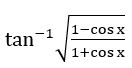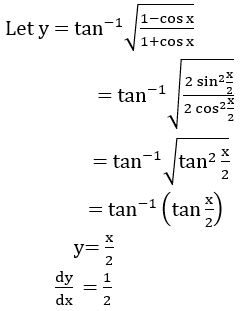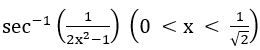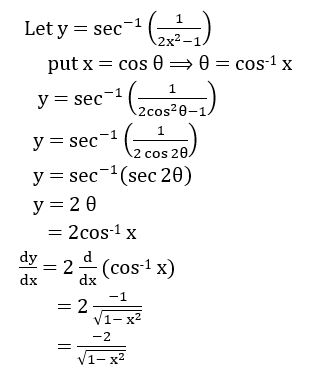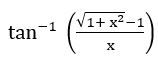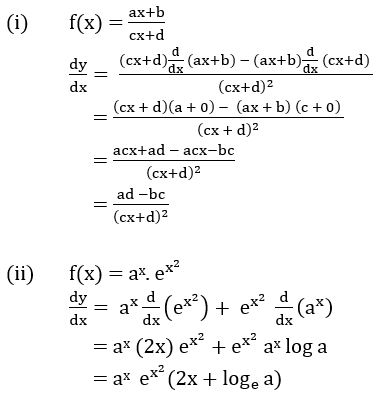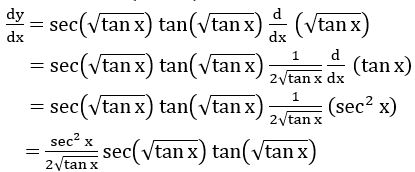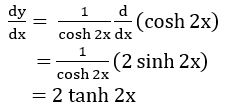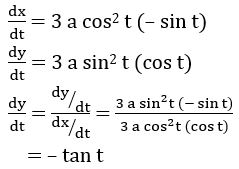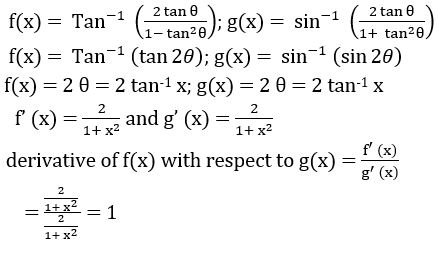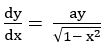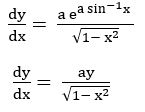Differentiation(2m Q & S) || V.S.A.Q’S||
Differentiation
This content was designed by the ‘Basics in Maths‘ team. These notes to do help intermediate First-year Maths students.
Inter Maths – 1B two mark questions and solutions are very useful in IPE examinations.
Differentiation
Question 1
Find f’ (x) for the following functions
(i) f(x) = (ax + b) (x > -b/a)
Sol:
Given f(x) = (ax + b) n
f’ (x) = n (ax + b) n – 1 ![]() (ax + b)
(ax + b)
= n (ax + b) n – 1 a
= an (ax + b) n – 1
(ii) f(x) = x2 2x log x
Sol:
Given f(x) = x2 2x log x
f’ (x) = ![]() (x2) 2x log x + x2
(x2) 2x log x + x2 ![]() (2x) log x + x2 2x
(2x) log x + x2 2x ![]() (log x).
(log x).
= 2×2x log x +x2 2x log a log x + x2 2x (1/x)
= x 2x[log x2 + x log x log 2 + 1]
Sol:
(iv) f(x) = log (sec x + tan x)
Sol:
Given, f(x) = log (sec x + tan x)
= sec x
Question 2
Find the derivative of the following functions
(i) f(x) = ex (x2 + 1)
Sol:
Given f(x) = ex (x2 + 1)
f’ (x) = ex ![]() (x2 + 1) + (x2 + 1)
(x2 + 1) + (x2 + 1) ![]() (ex)
(ex)
= ex (2x + 0) + (x2 + 1) ex
= ex (x2 + 2x + 1)
= ex (x + 1)2
(iii) cos (log x + ex)
(iv) x = tan (e-y)
e-y = tan-1 x
(v) cos [log (cot x)]
(vi) sin[tan-1(ex)]
(vii) cos-1(4x3 – 3x)
let y = cos-1(4x3 – 3x)
put x = cos θ ⟹ θ = cos-1 x
y = cos-1(4 cos 3 θ – 3cos θ)
= cos-1(cos 3θ)
= 3 θ
= 3 cos-1 x
Differentiation
Question 3
Find f’ (x), If f(x) = (x3 + 6 x2 + 12x – 13)100.
Sol:
Given f(x) = (x3 + 6 x2 + 12x – 13)100
f’ (x) = 100(x3 + 6 x2 + 12x – 13)99 ![]() (x3 + 6 x2 + 12x – 13)
(x3 + 6 x2 + 12x – 13)
= 100(x3 + 6 x2 + 12x – 13)99 (3x2 + 12 x + 12 – 0)
=100(x3 + 6 x2 + 12x – 13)99 3 (x2 + 4 x + 4)
= 300 (x + 2)2 (x3 + 6 x2 + 12x – 13)99
Question 4
If f(x) = 1 + x + x2 + x3 + …. + x100, then find f’ (1).
Sol:
Given f(x) = 1 + x + x2 + x3 + …. + x100
f’(x) = 0 + 1 + 2x + 3 x2 + … 100 x99
f’(1) = 1 + 2 + 3 + … + 100
= 50 × 101
= 5050
Question 5
From the following functions. Find their derivatives.
Question 6
Sol:
Question 7
Sol:
Given y = log (cosh 2x)
Question 8
If x = a cos3 t, y = a sin3 t, find
Sol:
Given If x = a cos3 t, y = a sin3 t
Question 9
Differentiate f(x) with respect to g(x) for the following.
derivative of f(x) with respect to g(x) =![]()
put x = tan θ ⟹ θ = tan-1 x
Question 10
Sol:
Visit My Youtube Channel: Click on below logo