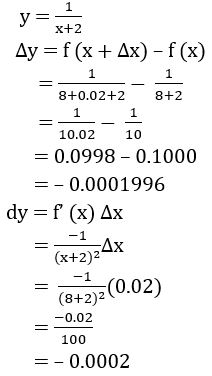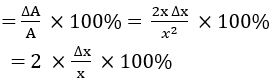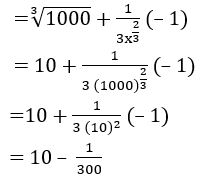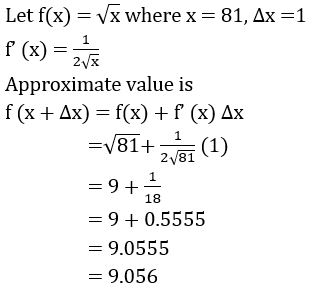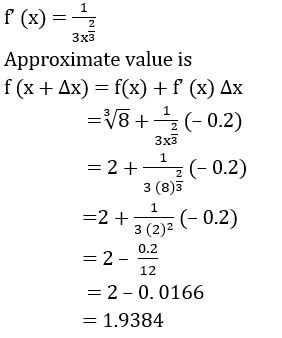Errors and Approximations || V.S.A.Q’S||

Errors and Approximations || V.S.A.Q’S||

Errors and approximations: These solutions were designed by the ‘Basics in Maths‘ team. These notes to do help intermediate First-year Maths students.

Inter Maths – 1B two mark questions and solutions are very useful in IPE examinations.

Errors and Approximations

Question 1

Find dy and ∆y for the following functions for the values of x and ∆x which are shown against each of the functions

(i) y = f(x) = x² + x at x = 10 when ∆x = 0.1.

Sol:

Given y = f(x) = x² + x at x = 10, ∆x = 0.1

∆y = f (x + ∆x) – f (x)

     = f (10 + 0.1) – f (10)

    = f (10.1) – f (10)

    = (10. 1)² + 10.1 – (10² + 10)

   = 102.01 + 10.1 – 100 – 10

    = 112.11 – 110

    = 2.11

dy = f’ (x) ∆x

     = (2x + 1) (0.1)

     = [2(10) + 1] (0.1)

    = 21 × 0.1

    = 2.1

(ii)  y = cos x at x = 60⁰ with ∆x = 1⁰ (1⁰ = 0.0174 radians)

Sol:

Given y = cos x, x = 60⁰ and ∆x = 1⁰

 ∆y = f (x + ∆x) – f (x)

      = cos (60⁰ + 1⁰) – cos 60⁰

      = cos (61⁰) – 0.5

      = 0.4848 – 0.5

      = – 0.0152

dy = f’ (x) ∆x

      = – sin x (1⁰)

      = – sin 60⁰ × 0.0174

      =– 0.8660 × 0.0174

      = – 0.0150

(iii)  y = x² + 3x + 6, x = 10 with ∆x = 0.01 

Sol:

   y = x² + 3x + 6

  ∆y = f (x + ∆x) – f (x)

       = f (10 + 0.01) – f (10)

       = f (10.01) – f (10)

      = (10.01)² + 3 (10.01) + 6 – (10² + 3 (10) + 6)

       = 100. 2001 + 30.03 + 6 – 100 – 30 – 6

       =130. 2301 – 130

       = 0.2301

dy = f’ (x) ∆x

     = (2x + 3 + 0) (0.01)

     = (2× 10 + 3) (0.01)

      = 23 × 0.01

      = 0.23

(iv)  y = , x = 8 and ∆x =0.02

Sol:

Question 2

The side of a square is increased from 3cm to 3.01cm find the approximate increase in the area of the square.

Sol:

Let x be the side of the square and the area be A

Area of the square A = x²

 x = 3 and ∆x = 0.01

∆A = 2x × ∆x

      = 2(3) (0.01)

      = 6 × 0.01

      = 0.06

Question 3

If an increase in the side of a square is 2% then find the approximate percentage of increase in its area.

Sol:

Let x be the side of the square and A be its area

 = 2

 A = x²

∆A = 2x × ∆x

The approximate percentage error in area A

= 2 × 2 =4

https://www.basicsinmaths.com/inter-mathematics-1a-and-1b-pdf-files/

Question 4

From the following. Find the approximations 

(i)

Sol:

Let f(x) =  , where x = 1000 and ∆x =– 1

f’ (x) =

Approximate value is

f (x + ∆x) = f(x) + f’ (x) ∆x

 = 10 – 0. 0033

 = 9.9967

(ii)

Sol:

(iii)

Sol:

(iv) Sin 62⁰

Sol:

Let f(x) = sin x, where x = 60⁰ and ∆x =2⁰

Approximate value is

 f (x + ∆x) = f(x) + f’ (x) ∆x

= sin 60⁰ + cos x (2⁰)

 = sin 60⁰+ cos 60⁰ (0.0348)

= 0.8660 + 0.5 × 0.0348

= 0.8660 + 0.0174

=0.8834

Question 5 

The radius of a sphere is measured as 14cm. Later it was found that there is an error of 0.02cm in measuring the radius. Find the approximate error in the surface area of the sphere.

Sol:

Given r = 14 cm and ∆r =0.02cm

Surface area of sphere =A = 4π r²

∆A = 8π r ∆r

      = 8 ×3.14× 14 × 0.02

      = 7.0336

Visit my Youtube Channel: Click on Below Logo