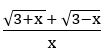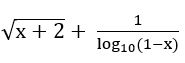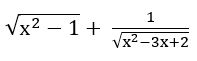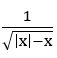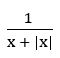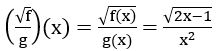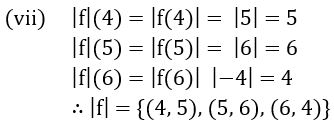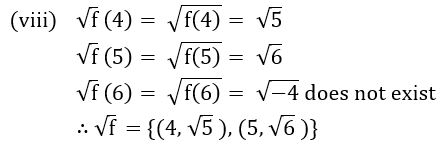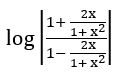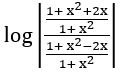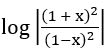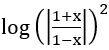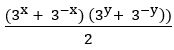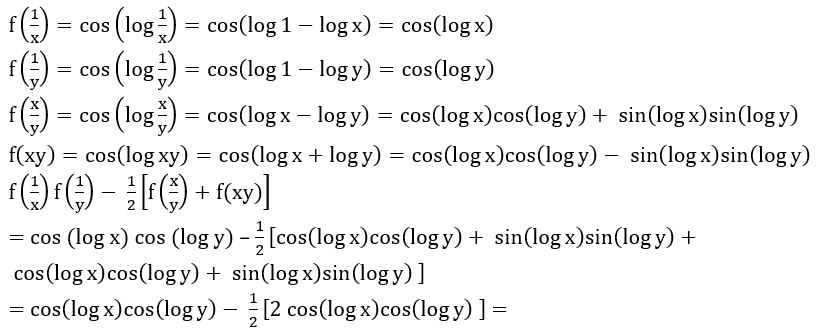Functions (2M Questions &Solutions)|| V.S.A.Q.’S||

Functions (2M Questions &Solutions)|| V.S.A.Q.’S||

Functions (2M Questions &Solutions): This note is designed by the ‘Basics in Maths’ team. These notes to do help intermediate First-year Maths students.

Inter Maths – 1A two marks questions and solutions are very useful in IPE examinations.

These notes cover all the topics covered in the intermediate First-year Maths syllabus and include plenty of solutions to help you solve all the major types of Math problems asked in the

IPE examinations.  

Functions

QUESTION 1

Find the Domain of the following real-valued functions.

(i) f(x) = 

Sol:   given f(x) =

         It is defined when 6x – x² – 5 ≠ 0

              ⇒ x² – 6x + 5 ≠ 0

                  x² – 5x – x + 5 ≠ 0 

                  x (x – 5) –1(x – 5) ≠ 0

                     (x – 5) (x – 1) ≠ 0

                      x ≠ 5 or x ≠ 1

                      ∴ domain = R – {1, 5}

(ii) f(x) =

Sol: Given f(x) =

  It is defined when 3 + x ≥ 0, 3 – x ≥ 0 and x ≠ 0

 ⇒ x ≥ –3, x ≤ 3 and x ≠ 0

       ⇒   –3≤ x, x ≤ 3 and x ≠ 0

       ⇒   –3≤ x ≤ 3 and x ≠ 0

              x ∈ [–3, 3] – {0}

        ∴ domain = [–3, 3] – {0}

(iii) f(x) =  

Sol: Given f(x) =

 It is defined when x + 2 ≥ 0, 1 – x > 0 and 1 – x ≠ 0

 ⇒ x ≥ –2, x < 1 and x ≠ 0 

  x ∈ [–2, ∞) ∩ (– ∞, 1) – {0}

 ⇒ x ∈ [–2, 1) – {0}

    ∴ domain = [–2, 1) – {0}

(iv) f(x) =

         Given f(x) =

         It is defined when 4x – x² ≥ 0

               ⇒ x² – 4x ≤ 0

                   x (x – 4) ≤ 0

                  (x – 0) (x – 4) ≤ 0

                  x ∈ [0, 4]

               ∴ domain = [0, 4]

(v) f(x) = log (x² – 4x + 3)

Given f(x) = log (x² – 4x + 3)

 It is defined when x² – 4x + 3 > 0

      ⇒   x² – 3x – x + 3 > 0

             x (x – 3) –1(x – 3) > 0

            (x – 3) (x – 1) > 0

          x ∈ (–∞, 1) ∪ (3, ∞)

          x ∈ R – [1, 3]

         ∴ domain = R – [1, 3]

(vi) f(x) =

    Given f(x) = It is defined when x² – 1 ≥ 0 and x² – 3x + 2 > 0  

(x + 1)(x – 1) ≥ 0 and x² – 2x – x + 2 > 0  

(x + 1) (x – 1) ≥ 0 and x (x – 2) (x – 1) > 0 

x∈ (–∞, –1) ∪ (1, ∞) and x ∈ (–∞, –1) ∪ (2, ∞)

            ∴ domain = R – (–1, 2]

(vii)  f(x) =

Given f(x) =

It is defined when  – x > 0

                                 ⇒ > x

                                 ⇒ x < 0

 ∴ domain = (–∞, 0)  

(viii) f(x) =

           Given f(x) =

        It is defined when  +x ≠0

                                 ⇒ ≠ – x

                                   ⇒ x > 0

         ∴ domain = (0, ∞)          

QUESTION 2

If f : R→ R , g : R → R defined by f (x ) = 4x – 1, g(x) = x² + 2 then find (i) (gof) (x) (ii) (gof) ()  (iii) (fof) (x)  (iv) go(fof) (0).

Sol: Given f(x) = 4x – 1, g(x) = x² + 2

(i)  (gof) (x) = g (f (x))

= g (4x – 1)

= (4x – 1)² + 2

= 16x² – 8x + 1 + 2

= 16x² – 8x + 3

(ii) (gof)  ()= (g (f ())

=  g(4() – 1)

= g (a + 1 – 1)

= g(a)

= a² + 2

(iii) (fof) (x) = f (f (x))

= f (4x – 1)

= 4 (4x – 1) – 1

= 16x – 4 – 1

= 16x – 5

(iv) go(fof) (0) = g(fof) (0)

= g (f (f (0)))

= g (f (– 1))

= g (– 4 – 1)

= g (– 5)

= (– 5)² + 2

= 25 + 2 = 27

QUESTION 3

If f and g are real valued functions defined by f(x) = 2x – 1 and g(x) = x², then find (i) (3f – 2g) (x) (ii) (fg)(x) (iii) (x) (iv) (f + g+ 2) (x)

Sol: Given f(x) = 2x – 1 and g(x) = x²

(i) (3f – 2g) (x) = 3f(x) – 2 g(x)

= 3(2x – 1) – 2(x²)

= 6x – 3 – 2x²

(ii) (fg)(x) = f(x) g(x)

= (2x – 1) (x²)

= 2x³ – 3x²

(iii) 

(iv) (f + g+ 2) (x) = f(x) + g(x) + 2

= 2x – 1 + x² + 2

= x² + 2x  + 1

QUESTION 4

If f = {(4, 5), (5, 6), (6, – 4)} g = {(4, – 4), (6, 5), (8,5)}, then find (i) f + g (ii) f – g (iii) 2f +4g (iv) f + 4 (v) fg (vi) f/g (vii) (viii)   (ix) f² (x) f³

Sol: Given f = {(4, 5), (5, 6), (6, – 4)}

  g = {(4, – 4), (6, 5), (8,5)} 

The domain of f ∩ The Domain of g = {4, 6}

(i) (f + g) (4) = f (4) + g (4)

                     = 5 – 4 = 1

     (f + g) (6) = f (6) + g (6)

                     =– 4 + 5 = 1

           ∴ f + g = {(4, 1), (6, 1)}                    

(ii) (f – g) (4) = f (4) – g (4)

                   = 5 – (– 4) = 5 + 4 = 9

(f – g) (6) = f (6) – g (6)

                   = – 4– 5   = – 9

         ∴ f – g   = {(4, 9), (6, – 9}

(iii) (2f +4g) (4) = 2 f (4) + 2 g (4)

                         = 2(5) + 4 (– 4)

                         = 10 – 16

                          =– 6

    (2f +4g) (6) = 2 f (6) + 2 g (6)

                         = 2(– 4) + 4 (5)

                         = – 8 + 20

                          =12

     ∴ (2f +4g) = {(4, – 6), (6, 12)}

(iv) (f + 4) (4) = f (4) + 4 = 5 + 4 = 9

       (f + 4) (5) = f (5) + 4 = 6 + 4 = 10

      (f + 4) (6) = f (6) + 4 = – 4 + 4 = 0

      ∴ (f + 4) = {(4, 9), (5, 10), (6, 0)}

(v) fg (4) = f (4) g (4) = (5) (– 4) =– 20

      fg (6) = f (6) g (6) = (– 4) (5) =– 20

      ∴ fg = {(4, – 20), (6, – 20)}

(vi) f/g (4) = f(4)/g(4) = 5/ – 4 = – 5/4

       f/g (6) = f(6)/g(6) = – 4/ 5

     ∴ f/g = {(4, – 5/4), (6, – 4/ 5)}

(ix) f²(4) = (f (4))² = (5)² = 25

       f²(5) = (f (5))² = (6)² = 36  

       f²(6) = (f (6))² = (– 4)² = 16

     ∴ f² = {(4, 25), (5, 36), (6, 16)}

(x) f³(4) = (f (4))³ = (5)³ = 125

     f³(5) = (f (5))³ = (6)³ = 216  

     f³(6) = (f (6))³ = (– 4)³ = –64

   ∴ f³ = {(4, 125), (5, 216), (6, –64)}

QUESTION 5

If A = {0, π/6, π/4, π/3, π/2} and f: A→ B is a surjection defined by f(x) = cos x, then find B.

 Sol: Given A = {0, π/6, π/4, π/3, π/2}

            f(x) = cos x

          f (0) = cos (0) = 1

          f(π/6) = cos (π/6) =

          f(π/4) = cos (π/4) =

          f(π/3) = cos (π/3) = 1/2

          f(π/2) = cos (π/2) = 0

∴ B = {1, , , ½, 0}

QUESTION 6

If A = {–2, –1, 0, 1, 2} and f: A→ B is a surjection defined by f(x) =x² + x + 1, then find B.

Sol: Given A = {–2, –1, 0, 1, 2} and f(x) = x² + x + 1

   f (–2) = (–2)² + (–2) + 1= 4 – 2 + 1 = 3

    f (–1) = (–1)² + (–1) + 1= 1 – 1 + 1 = 1

    f (0) = (0)² + (0) + 1= 0 + 0 + 1 = 1

    f (1) = (1)² + (1) + 1= 1 + 1 + 1 = 3

    f (2) = (2)² + (2) + 1= 4 + 2 + 1 = 7

        ∴ B = {1, 3, 7}

QUESTION 7

If A = {1, 2, 3, 4} and f: A→ B is a surjection defined by f(x) = then find B.

 Sol: Given A = {1, 2, 3, 4} and f(x) =

QUESTION 8

If f(x) = 2, g(x) = x², h(x) = 2x ∀ x ∈ R, then find (fo(goh)) (x)

Sol: Given f(x) = 2, g(x) = x², h(x) = 2x

(fo(goh)) (x) = fo (g (h (x))

                          = f (g (h (x))

                           = f(g(2x)

                           = f((2x)²)

                           = f(4x²) = 2

QUESTION 9

If f: R→ R, g: R → R defined by f (x) = 3x – 2, g(x) = x² +1 then find (i) (gof^-1) (2) (ii) (gof) (x – 1) 

Sol: Given f: R→ R, g: R → R defined by f (x) = 3x – 2, g(x) = x² +1

(i) Let y = f(x) ⟹ x = f^-1(y)

      y = 3x – 2

     y + 2 = 3x

    x = (y + 2)/3

f^-1(y) = (y + 2)/3

∴ f^-1(x) = (x + 2)/3

  Now 

(gof^-1) (2) = g(f^-1(2))

                = g ((2 + 2)/3)

               = g (4/3)

              = (4/3)² + 1 = 16/9 + 1 = 25/9

(ii) (gof) (x – 1) = g (f (x – 1))

                        = g [ 3(x – 1) – 2)]

                        = g (3x – 3 – 2)

                        =g (3x – 5)

                        = (3x – 5)² + 1

                        = 9x² – 30x + 25 + 1

                       = 9x² – 30x + 26

QUESTION 10

If f: N→ N defined by f (x) = 2x + 5, Is onto? Explain with reason.

Sol: Given f (x) = 2x + 5

 Let y = f(x) ⟹ x = f^-1(y)

y = 2x + 5

2x = y – 5

 x = (y – 5)/2 ∉ N

∴ f(x) is not onto 

QUESTION 11

Find the inverse of the following functions

(i) If a, b ∈ R, f: R→ R defined by f(x) = ax + b

    Given function is f(x) = ax + b

   Let y = f(x) ⟹ x = f^-1(y)

      y = ax + b

     y – b = ax

    x = (y – b)/a

f^-1(y) = (y – b)/a

∴ f^-1(x) = (x – b)/a

(ii) f: R→ (0, ∞) defined by f(x) = 5^x

    Given function is f(x) = 5^x

   Let y = f(x) ⟹ x = f^-1(y)

        y = 5^x

        x =

   f^-1(y) =

    ∴ f^-1(x) =

(iii) f: (0, ∞) → R defined by f(x) =

    Given function is f(x) =

     Let y = f(x) ⟹ x = f^-1(y)

    y =

   x = 2^y

  f^-1(y) = 2^y

  ∴ f^-1(x) = 2^x

(iv) f: R→ R defined by f(x) = e^{4x + 7}

     Given function is f(x) = e^{4x + 7}

   Let y = f(x) ⟹ x = f^-1(y)

  y = e^{4x + 7}

  4x + 7 =

  4x =   – 7

  x = (  – 7)/4

  f^-1(y) = (  – 7)/4

 ∴ f^-1(x) = (  – 7)/4

(v) f: R→ R defined by f(x) = (2x + 1)/3

   Given function is f(x) = (2x + 1)/3

  Let y = f(x) ⟹ x = f^-1(y)

 y= (2x + 1)/3

 3y = 2x + 1

 2x = 3y – 1

  x = (3y – 1)/2

 f^-1(y) = (3y – 1)/2

 ∴ f^-1(x) = (3x – 1)/2

QUESTION 12

If f: R→ R defined by f(x) =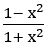 , then show that f (tan θ) = cos 2θ

Sol: Given function is f(x) =

        f (tan θ) =

   ∴  f (tan θ) = cos 2θ                           

QUESTION 13  

If f: R – {±1} → R defined by f(x) =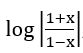 , then show that = 2f (x)

Sol: Given f(x) =

          =

                          =

                          =

=

                          =

                           = 2

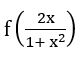    ∴ = 2f (x)

QUESTION 14

If the function f: R→ R defined by f(x) =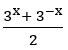 , then show that f (x + y) + f (x – y) = 2 f(x) f(y).

Sol: Given function is f(x) =

f (x + y) + f (x – y) = 

 =  

=

= 

=

=2

∴ f (x + y) + f (x – y) = 2 f(x) f(y)

QUESTION 15

If f(x) = cos (log x), then show that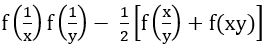 = 0

Sol: Given function is f(x) = cos (log x)

 = cos (log x) cos (log y) – cos (log x) cos (log y)

= 0

Hence proved

QUESTION 16

Find the range of the following real-valued functions

Sol:

(i) f(x) =

     Given function is f(x) =

    Let y =

    ⟹ e^y =

       e^y > 0

∴ The range of f(x) is R

(ii) f(x) =

     It is defined when x – 2 ≠ 0

     ⟹ x ≠ 2

    Domain = R – {2}                 

    let y =

          =

         y = x + 2

  if x = 2 ⟹ y = 4

 ∴ Range of f(x) is R – {4}

QUESTION 17

Find the domain and range of the following real-valued functions

Sol:

(i) f(x) =

It is defined when 1 + x² ≠ 0

  ⟹ x² ≠ – 1

    x ∈ R

   ∴ domain of f(x) is R

  Let y =

      y (1 + x²) = x

     y + x²y = x

     x² y – x + y = 0

   x =

It is defined when 1 – 4y² ≥ 0 and 2y ≠ 0

    ⟹ 4y² – 1 ≤ 0 and y ≠ 0     

        (2y – 1) (2y + 1) ≤ 0 and y ≠ 0 

        (y – 1/2) (y + 1/2) ≤ 0 and y ≠ 0 

  –  ½≤ y ≤ ½ and y ≠ 0 

    ∴ Range of f(x) is [– ½, ½] – {0}    

(ii) f(x) = 

      It is defined when 9 – x² ≥ 0

     ⟹ x² – 9 ≤ 0

       (x + 3) (x – 3) ≤ 0

   –  3 ≤ y ≤ 3  

∴ the domain of f (x) is [– 3, 3]

  Let y =

       y² = 9 – x²

       x² = 9 – y²

       x =

      It is defined when 9 – y² ≥ 0

     ⟹ y² – 9 ≤ 0

       (y + 3) (y – 3) ≤ 0

     –  3 ≤ y ≤ 3  

         y ∈ [– 3, 3]

  ∴ Range of f (x) is [0, 3] (∵ y ≥ 0)

(iii) f(x) =

     clearly, x ∈ R

    ∴ domain of f(x) is R

        Let y =

       If x = 0, then y = 1

       If x = – 1, then y = 1

       If x = 1, then y = 3

      If x = – 2, then y = 3

      If x = 2, then y = 5

      ∴ Range of f (x) is [1, ∞)

(iv) f(x) = [x]

clearly Domain = R  and Range = Z     

QUESTION 18.

Define (i) One – One function (ii) Onto function (iii) Bijection (iv) Even and Odd functions

     (i) One – One Function: one – one, if every element of A has a unique image in B.

    (ii) Onto function: A function f: A→ B is said to be onto if ∀ y ∈ B there exists x ∈ A such that f(x) = y.

    (iii) Bijection: A function f: A→ B is said to be a Bijection if it is both one-one and onto.

    (iv) Even and Odd functions:

     If f(–x) = f(x), then f(x) is even function

          If f(– x)

= – f(x), then f(x) is odd function

Visit my Youtube Channel: Click on Below Logo