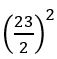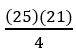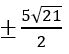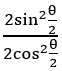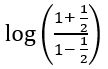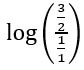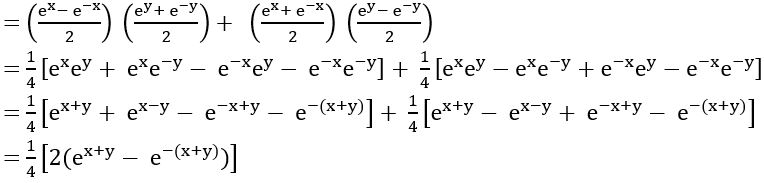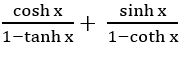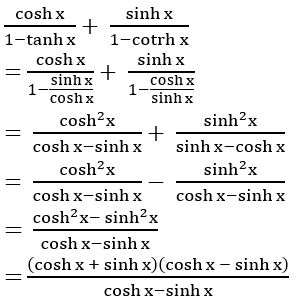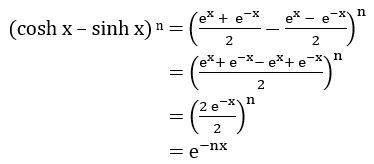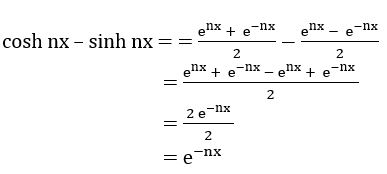Hyperbolic Functions V.S.A.Q.’S || 2 Marks

Hyperbolic Functions V.S.A.Q.’Sdesigned by the ‘Basics in Maths‘ team. These notes to do help the intermediate First-year Maths students.

Inter Maths – 1A  Hyperbolic Functionstwo marks questions and solutions are very useful in IPE examinations.

Hyperbolic Functions

Question 1

Prove that for any x∈ R, sinh (3x) = 3 sinh x + 4 sinh³ x

Sol:

sinh (3x) = sinh (2x + x)

                  = sinh 2x cosh x + cosh 2x sinh x

                 = (2 sinh x cosh x) cosh x + (1 + 2 sinh² x) sinh x

                 = 2sinh x cosh² x + sinh x + 2 sinh³ x

                 = 2 sinh x (1 + sinh² x) + sinh x + 2 sinh³ x

                 = 2 sinh x + 2 sinh³ x+ sinh x + 2 sinh³ x

                 = 3 sinh x + 4 sinh³ x

Question 2

If cosh x = , find the values of (i) cosh 2x and (ii) sinh 2x

Sol:

Given cosh x =

 Cosh 2x = 2 cosh² x – 1

                 = 2.  – 1

                 =

Sinh² 2x = cosh² 2x – 1

                 = – 1

                 =  – 1

       =

  Sinh² 2x   =

Question 3

If cosh x = sec θ then prove that tanh²= tan²

Sol:

tanh²  =

              =

             =

             =

             = tan²

Question 4

If sinh x = 5, then show that x =

Sol:

Given, sinh x = 5

      ⟹ x = sinh^-15    

We know that sinh^-1x =  

        ⟹ x =       

               x  = 

Question 5

Show that tanh^-1 =   log3

Sol:

Given tanh^-1

We know that tanh^-1 x =    

 tanh^-1  =   

                 =    

                 =   log3

Question 6

For x, y ∈ R prove that sinh (x + y) = sinh (x) cosh (y) + cosh (x) sinh (y)

Sol:

R.H.S = sinh (x) cosh (y) + cosh (x) sinh (y)

=  

= sinh (x + y)

Question 7

For any x∈ R, prove that cosh⁴ x – sinh⁴ x = cosh 2x

Sol:

cosh⁴ x – sinh⁴ x = (cosh² x)² – (sinh² x)²

                                 = (cosh² x + sinh² x) (cosh² x – sinh² x)

                                 = 1. cosh 2x

                                 = cosh 2x

Question 8

Prove that = cosh x + sinh x

Sol:

= cosh x + sinh x

Question 9

If sin hx = ¾ find cosh 2x and sinh 2x.

Sol:

Given sin hx = ¾

We know that cosh² x = 1 + sinh² x

                                           = 1 + (3/4)²

                                           = 1 + 9/16

                                           = 25/16

cos hx = 5/4

cosh 2x = 2cosh² x – 1

                = 2(25/16) – 1

                = 25/8 – 1

                = 17/8

Sinh 2x = 2 sinh x cosh x

                = 2 (3/4) (5/4)

                = 15/8

Question 10

Prove that (cosh x – sinh x) ⁿ = cosh nx – sinh nx

Sol:

∴ (cosh x – sinh x) ⁿ = cosh nx – sinh nx

Visit My YouTube Channel:  Click on below logo