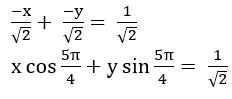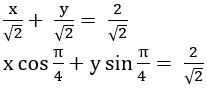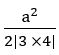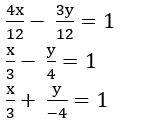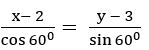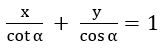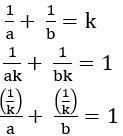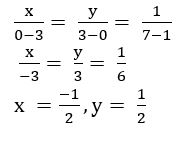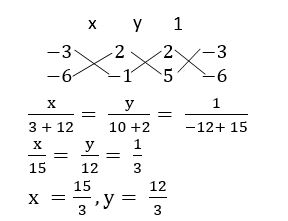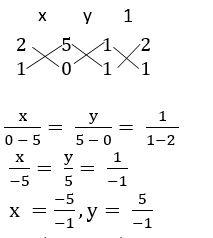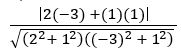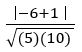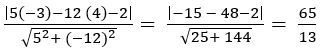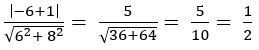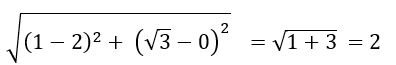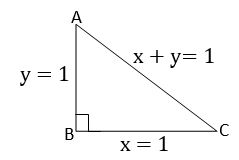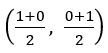This note is designed by the ‘Basics in Maths’ team. These notes to do help the intermediate First-year Maths students.

Inter Maths – 1B two mark questions and solutions are very useful in IPE examinations.

These notes cover all the topics covered in the intermediate First-year Maths syllabus and include plenty of solutions to help you solve all the major types of Math problems asked in the IPE examinations.  

Straight Lines

QUESTION1.

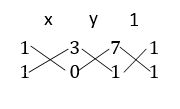
Prove that the points (1, 11), (2, 15), and (– 3, – 5) are collinear, and find the equation of the line containing them.

Sol:

 Let A (1, 11), B (2, 15), and C (– 3, – 5)

 The slope of the line segment joining the points (x₁, y₁) and (x₂, y₂) is

  Slope of AB  = = 4

  Slope of BC = =  = 4

QUESTION2.

Find the condition for the points (a, 0), (h, k), and (0, b) to be collinear.

Sol:

Let A (a, 0), B (h, k) and C (0, b)

The slope of the line segment joining the points (x₁, y₁) and (x₂, y₂) is Given that A, B, and C are collinear points

  The slope of AB = The slope of BC

          ⟹   

          ⟹   

          ⟹ – hk = (h – a) ( b – k)

                  – hk = hb – hk – ab + ak

           ⟹ 0 = hb + ak – ab

           ⟹ hb + ak = ab or

QUESTION3.

Find the equations of the straight lines which makes intercepts whose sum is sum is 5 and product is 6.

Sol:

The equation of the line in the intercept form is

   Given that, a + b = 5 and ab = 6

         ⟹   b = 5 – a

           a(5 – a) = 6

         5a – a² = 6

          a² – 5a + 6 = 0

        a – 3a – 2a + 6 = 0

       a (a – 3) – 2(a – 3) = 0

       (a – 3) (a – 2) = 0

       a = 3 or a = 2  

case (i) if a = 3 ⟹ b = 2

              ⟹ 2x + 3y – 6 = 0

case (ii) if a = 2 ⟹ b = 3

               = 1    ⟹ 3x + 2y – 6 = 0

QUESTION4.

Find the equation of the straight line which makes an angle 135⁰ with the positive X – axis measured countered clockwise and passing through the point (– 2, 3).

Sol:

Slope of the line m = tan 135⁰ = – 1

         The point is (– 2, 3)

 The equation of the straight line in slope point form is (y – y₁) = m (x – x₁)

The equation of the line passing through the point (– 2, 3) with slope – 1 is

 y – 3 = – 1 (x + 2)

 y – 3 =– x – 2

x + y – 1 = 0

QUESTION5.

Find the equation of the straight line passing through the points (1, – 2) and (– 2, 3).

Sol:

Given points are (1, – 2), (– 2, 3)

 The equation of the straight line in two points form is (y – y₁) = (x – x₁)

 The equation of required straight line is

        (y + 2) =  (x – 1)

         (y + 2) =  (x – 1)

         – 3 (y + 2) = 5 (x – 1)

          – 3y – 6 = 5x – 5

         5x + 3y + 1 = 0

QUESTION6.

Find the slopes of the line x + y = 0 and x – y = 0

Sol:

The slope of the line ax + by + c = 0 is

The slope of the line x + y = 0 is  = – 1

The slope of the line x – y = 0 is  = 1

QUESTION7.

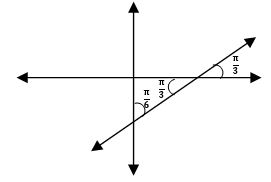
Find the angle which the straight-line y = x – 4 makes with the Y-axis.

Sol:

Given equation is y = x – 4

        Compare with y = mx + c

          m =  ⟹ tan θ =
         θ =

      Angle made by the line with X-axis is

      Angle made by the line with Y-axis is

QUESTION8.

Find the equation of the reflection of the line x = 1 in the Y-axis.

Sol:

Given equation is     x = 1

 Reflection about the Y-axis is x =– 1

 Required equation of the line is x + 1 = 0

QUESTION9.

Write the equations of the straight lines parallel to X-axis and (i) at a distance of 3 units above the X-axis and (ii) at a distance of 4 units below the X-axis.

Sol:

(i) The equation of the straight line parallel to X-axis which is at a distance of 3 units above the X-axis is y = 3

        ⟹ y – 3 = 0

 (ii) The equation of the straight line parallel to X-axis which is at a distance of 4   units below the X-axis is y = – 4

         ⟹ y + 4 = 0

QUESTION10.

Write the equations of the straight lines parallel to the Y-axis and (i) at a distance of 2 units from the Y-axis to the right of it (ii) at a distance of 5 units from the Y-axis to the left of it.

Sol:

(i) The equation of the straight line parallel to the Y-axis which is at a distance of 2 units from the Y-axis to the right of it is x = 2

                                                                          ⟹ x – 2 = 0

 (ii) The equation of the straight line parallel to the Y-axis which is at a distance of 5 units from the Y-axis to the left of it is x =– 5

                              ⟹ x + 5 = 0

QUESTION 11.

Find the value of x, if the slope of the line passing through (2, 5) and (x, 3) is 2.

Sol:

Given the slope of the line passing through (2, 5) and (x, 3) is 2.

 The slope of the line segment joining the points (x₁, y₁) and (x₂, y₂) is

       ⟹ = 2

       ⟹ 2(x – 2) = – 2

       x – 2 = – 1  

       x = 1

QUESTION 12.

Find the equation of the straight line passing through (– 4, 5) and making non – zero intercepts on the coordinate axes whose sum is zero.

Sol:

The equation of a line in the intercept form is

         Given a = b

         ⟹ = 1

         ⟹

              x + y = a

     but it is passing through (– 4, 5)

           – 4+ 5 = a

             a = 1

    ∴ The equation of the required straight line is x + y = 1

         x + y – 1 = 0

QUESTION13.

Find the equation of the straight line passing through (– 2, 5) and cutting off equal and non – zero intercepts on the coordinate axes.

Sol:

The equation of a line in the intercept form is

         Given a + b = 0

                     b = – a

         ⟹

         ⟹  

                     x – y = a

    but it is passing through (– 2, 4)

           – 2– 4 = a

             a = –6

    ∴ The equation of the required straight line is x – y = –6

         x + y + 6 = 0

QUESTION14.

Find the equation of the straight line whose distance from the origin is 4, if the normal ray from the origin to the straight line makes an angle of 135⁰ with  the positive direction of X – axis

Sol:

The equation of the straight line in the normal form is x cos α + y sin α = p

        p = 4 and α = 135⁰

        x cos 135⁰ + y sin 135⁰ = 4

        x  + y  = 4

        = 4

  – x + y = 4

   x – y + 4 = 0

QUESTION15.

Write the parametric equation of the straight line passing through the point (3, 2) and making an angle 135⁰ with the positive direction of the X – axis.

Sol:

Given θ = 135⁰ and (h, k) = (3, 2)

  The parametric equations are: x = h + r Cos θ, y = k +r Sin θ

x = 3 + r Cos 135⁰, y = 2 + r Sin 135⁰

         x = 3 –  , y = 2 +

QUESTION16.

Transform the following equation into normal form.

(i)  x + y +1 = 0

 Sol: 

Given equation is x + y +1 = 0

    x + y =– 1

  – x – y = 1

  Dividing on both sides by

(ii) x + y = 2

 Sol: 

 Given equation is x + y = 2

  Dividing on both sides by

QUESTION 17.

If the area of the triangle formed by the straight lines x = 0, y = 0 and 3x + 4y =a (a > 0) is 6 square units. Find the value of ‘a’.

Sol:

Given equation is 3x + 4y = a

 The area of the triangle formed by the straight-line ax + by + c = 0 with the coordinate axes is

        ⟹ = 6

              = 6

            a² = 24 ⟹ a = 12(∵ a > 0)

QUESTION18.

Find the sum of the squares of the intercepts of the line 4x – 3y = 12

Sol:

Given equation is 4x – 3y = 12    

       It is in the form of   

        a = 3 and b =– 4

the sum of the squares of intercepts = a² + b ²

      = 3² + (– 4)²

      = 9 + 16 = 25

QUESTION 19.

Find the angle made by the straight – line y = – x + 3 with the positive direction of the X-axis measured in the counter-clockwise direction.

Sol:

Give equation of straight line is y =   x + 3

 It is in the form of y = mx + c

                                   m =

                                 tan θ =

                         ⟹ θ =

QUESTION 20.

Find the equation of the straight line in the symmetric form, given the slope and point on the line (2, 3).

Sol:

Equation of the line in the symmetric form is

 Given Point (x₁, y₁) = (2, 3) and slope m =    

tan θ =

⟹ θ = 60⁰

 ∴ The equation of the line is

QUESTION 21.

If the product of the intercepts made by the straight-line x tan α + y sec α = 1 (0≤ α < π/2) on the coordinate axes is equal to sin α, find α.

Sol:

Given equation is x tan α + y sec α = 1

It is in the form of

 a = cot α, b = cos α

product of intercepts = sin α

⟹ ab = sin α

       cot α.cos α = sin α

       (cos α)/ (sin α). cos α = sin α

       ⟹ cos² α = sin² α

        ⟹ tan² α = 1

              tan α = 1(∵ 0≤ α < π/2)

     ∴ α = 45⁰

QUESTION22.

If the sum of the reciprocals of the intercepts made by a variable straight–line on the axes of coordinates is a constant, then prove that the line always passes through a fixed point.

Sol:

The equation of the line in the intercept form is

Let the sum of the reciprocals of intercepts is k

  ⟹

   ∴ the line always passes through a fixed point (1/k, 1/k).

QUESTION23.

Find the ratio in which the straight-line 2x + 3y – 20 = 0 divides the join of the points (2, 3) and (2, 10).

Sol:

Given equation is L ≡ 2x + 3y – 20 = 0

      L₁₁ = 2(2) + 3(3) = 4 + 9– 20 = – 7

      L₂₂ = 2(2) + 3(10) = 4 + 30 – 20 = 14

 We know that the line L = 0 divides the line joining the points (x₁, y₁) and (x₂, y₂) in the ratio – L₁₁ : L₂₂

                      = – (– 7) : 14

                      = 1 : 2

QUESTION24.

State whether (3, 2) (– 4, – 3) are on the same or opposite sides of the straight-line 2x – 3y + 4 = 0.

Sol:

Given equation is L ≡ 2x – 3y + 4 = 0

 L₁₁ = 2(3) – 3(2) + 4 = 6 – 6 + 4 = 4 > 0

 L₂₂ = 2(– 4) – 3(–3) + 4 = – 8 + 9 + 4 = 5 > 0

     L₁₁, L₂₂ has the Same sign

    ∴ Given points lies the same side of the line 2x – 3y + 4 = 0.

QUESTION25.

Find the ratio in which (i) X-axis and (ii) Y-axis divide the line segment  joining A (2, –3) and B (3, – 6)

Sol:

(i) X – axis divide in the ratio – y₁ : y₂  = – ( –3) : – 6 = – 1 : 2

(ii) Y – axis in the ratio – x₁ : x_{2 =}  – 2 : 3 = – 2 : 3

QUESTION26.

Find the equation of the straight line passing through the point of intersection of the lines x + y + 1 = 0 and 2x – y + 5 = 0 and containing the point (5, – 2).

Sol:

 Given equations are

         x + y + 1 = 0 ……… (1)

         2x – y + 5 = 0……. (2)

       The equation of the line passing through the point of intersection of the lines L₁ = 0 and L₂ = 0 is L₁ + λ L₂ = 0

     The equation of the line passing through the point of intersection of the lines (1) and (2) is

      x + y + 1 + λ (2x – y + 5) = 0

     but the line passes through (5, – 2)

      5 – 2 + 1 + λ (2(5) – (– 2) + 5) = 0

      4 + λ (10 + 2 + 5) = 0

       4 + λ (17) = 0

         λ = –4 /17

∴ the equation of required line is

        x + y + 1 + (–4 /17) (2x – y + 5) = 0

       17(x + y + 1) –4 (2x – y + 5) = 0

        17x + 17y + 17 – 8x + 4y – 20 = 0

        9x + 21y – 3 = 0

        3x + 7y – 1 = 0

QUESTION27.

If a, b, and c are in arithmetic progression, then show that the equation ax + by + c = 0 represents a family of concurrent lines and find the point of concurrency.

Sol:

Given, a, b, and c are in A.P. and the equation is ax + by + c = 0

  a, b, and c are in A.P.

   ⟹ b = (a + c)/2

  Substitute b value in the equation ax + by + c = 0

   ⟹  ax + [ (a + c)/2]y + c = 0

   ax + ay/2 + cy/2 + c = 0

  a(x + y/2) + c(y/2 + 1) = 0

 dividing on both sides by a

  ⟹ (x + y/2) + (c/a) (y/2 + 1) = 0

 It is in the form of L₁ + λ L₂ = 0

  ∴ given equation represent a family of concurrent lines

  x + y/2 = 0 and y/2 + 1 = 0 are the lines

  y/2 + 1 = 0 ⟹ y/2 = – 1

y =– 2 ⟹ x = 1

The point of concurrency is (– 2, 1)    

QUESTION28.

Find the point of intersection of the line 7x + y + 3 = 0 and x + y = 0

Sol:

Given equations are 7x + y + 3 = 0 and x + y = 0

 ∴ The point of intersection is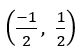

QUESTION29.

Transform the following equations into the form L₁ + λ L₂ = 0 and find the point of concurrency of the family of straight lines represented by the equation.

(i) (2 + 5k) x – 3 (1 + 2k) y + (2 – k) = 0

     Given equation is

  (2 + 5k) x – 3 (1 + 2k) y + (2 – k) = 0

 2x + 5kx – 3y – 6ky + 2 – k = 0

 2x – 3y + 2 + k (5x – 6y – 1) = 0

 It is in the form of L₁ + λ L₂ = 0 L₁ ≡ 2x – 3y + 2 = 0 and L₂≡ 5x – 6y – 1 = 0

By solving above equations, we get point of concurrency

∴ The point of concurrency is (5, 4)

(ii) ( k + 1) x + (k + 2) y + 5 = 0

 Given equation is  (k + 1) x + (k + 2) y + 5 = 0

  kx + x + ky + 2y + 5 = 0

 x + 2y + 5 + k (x + y) = 0

 It is in the form of L₁ + λ L₂ = 0

  L₁ ≡ x + 2y + 5 = 0 and L₂≡ x + y = 0

By solving the above equations, we get point of concurrency

 ∴ The point of concurrency is (5, – 5)

QUESTION30.

Find the value of ‘p’, if the straight lines x + p = 0, y + 2 = 0 and 3x + 2y + 5 = 0 are concurrent.

Sol:

Given that x + p = 0 —— (1), y + 2 = 0 —— (2) and 3x + 2y + 5 = 0 —— (3)   are concurrent.

       From (1) x + p = 0 ⟹ x = – p

        From (2) y + 2 = 0 ⟹ y = – 2

       Point of intersection of (1) and (2) is (– p, – 2)

       From (3)

         3y + 2x + 5 = 0

         3(– p) + 2 (– 2) + 5 = 0

           – 3p – 4 + 5 = 0

            – 3p + 1 = 0

                3p = 1

                  p = 1/3

QUESTION31.

Find the area of the triangle formed by the following straight lines and the coordinate axes.

(i) x – 4y + 2 = 0

The area of the triangle formed by the straight-line ax + by + c = 0 with the coordinate axes is

 The area of the triangle formed by the straight-line x – 4y + 2 = 0    with the coordinate axes is  =  

(ii) 3x – 4y + 12 = 0   

The area of the triangle formed by the straight-line 3x – 4y + 12 = 0 with the coordinate axes is  =

QUESTION32.

Find the angle between the lines 2x + y + 4 = 0 and y – 3x =7

Sol:

Given Equations are 2x + y + 4 = 0 and y – 3x =7

  If θ is the angle between the lines a₁x + b₁y + c = 0 and a₂x + b₂y + c = 0, then  cos θ =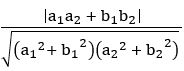

⟹   cos θ =

                  =

                  =

          cos θ =

∴ θ = 45⁰

QUESTION33.

Find the perpendicular distance from the point (– 3, 4) to the straight line 5x – 12y = 2

Sol:

Given equation is 5x – 12y = 2 ⟹ 5x – 12y – 2 = 0

The perpendicular distance from the point (x₁, y₁) to the straight-line ax + by + c = 0 is

The perpendicular distance from the point (– 3, 4) to the straight-line 5x – 12y – 2 = 0 is

 = 5

QUESTION34.

Find the distance between the parallel lines 3x + 4y – 3 = 0 and 6x + 8y – 1 = 0

Sol:

Given equations are 3x + 4y – 3 = 0 and 6x + 8y – 1 = 0

3x + 4y – 3 = 0 ⟹ 2(3x + 4y – 3) = 2(0) (multiplying on both sides by 2)

         ⟹ 6x + 8y – 6 = 0

 The distance between two parallel lines ax + by + c₁ =0 and ax + by + c₂ =0 is

The distance between two parallel lines 6x + 8y – 6 = 0 and 6x + 8y – 1 = 0 is

QUESTION35.

Find the foot of the perpendicular from (– 1, 3) on the straight line 5x – y – 18 = 0

Sol:

Let (h, k) be the foot of the perpendicular from (– 1, 3) on the straight line 5x – y – 18 = 0

If (h, k) is the foot of the perpendicular from (x₁, y₁) on the straight-line ax + by + c = 0, then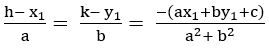

⟹

⟹

⟹

      h+ 1 = 5 and k – 3 = – 1

      h = 4 and k = 2

   ∴ (h, k) = (4, 2)

QUESTION36.

Find the image of (1, – 2) with respect to the straight line 2x – 3y + 5 = 0

Sol:

Let  (h, k) be the image of (1, – 2) with respect to the straight line 2x – 3y + 5 = 0

If (h, k) is the image of the point (x₁, y₁) with respect to the straight line ax + by + c = 0, then

If (h, k) is the image of (1, – 2) with respect to the straight line 2x – 3y + 5 = 0,        

⟹

⟹

⟹

      h – 1 = – 4 and k + 2 = 6

      h =– 3 and k = 4

   ∴ (h, k) = (– 3, 4)

QUESTION37.

If 2x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining (3, –4) and (α, β), find α + β.

Sol:

Given 2x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining (3, –4) and (α, β)

     ⟹ (α, β) is the image of (3, –4) concerning the straight line 2x – 3y – 5 = 0

    ⟹

        α – 3 = – 4 and β + 4 = 6

        α = – 1 and β = 2

         α + β = – 1 + 2 = 1

QUESTION38.

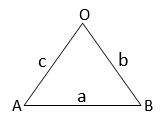
Find the incenter of the triangle whose vertices are (1, ), (2, 0) and (0, 0)

Sol:

Let O = (0, 0), A = (1, ) and B = (2, 0)

 a = AB =    

b = OB =

c = OA =   

in centre of a triangle with sides a, b and c, whose vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃) is

In centre of ∆ OAB =

                                    =

                                    = =

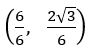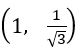
QUESTION39.

Find the ortho centre of the triangle whose sides are given by x + y + 10 = 0, x – y – 2 = 0 and 2x + y – 7 = 0.

Sol:

Given equations are

x + y + 10 = 0 …… (1)

x – y – 2 = 0 …… (2)

2x + y – 7 = 0. …… (3)

   Slope of the line (1) is – 1

   Slope of the line (2) is 1

   The straight lines (1) and (2) are perpendicular lines

   The point of intersection of (1) and (2) is the orthocenter

 x + y = – 10 ⟹ y = – 10 – x

  from (2) x – y – 2 = 0

                  x – (– 10 – x) – 2 = 0

                 x + 10 + x – 2 = 0

               2x + 8 = 0 ⟹ x = – 4

            ⟹ y = – 10 + 4 = – 6

                ∴ Orthocenter is (– 4, – 6)

QUESTION40.

Find the circum centre of the triangle whose sides are x = 1, y = 1 and x + y = 1

Sol:

Given equations are x = 1, y = 1 and x + y = 1

       A = (1, 0), B = (1, 1) and C = (0, 1)

     AB and BC are perpendicular lines

      Circum centre is the midpoint of hypotenuse

      i.e., midpoint of AC

  ∴ Circum centre =  

                                =

Visit My Youtube Channel:  Click  on below  logo