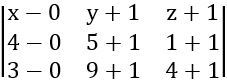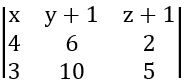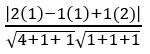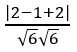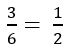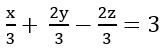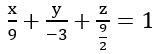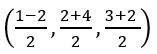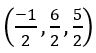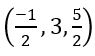The Plane (2m Questions & Solutions) || V.S.A.Q’S||
The Plane: These solutions were designed by the ‘Basics in Maths’ team. These notes to do help intermediate First-year Maths students.
Inter Maths – 1B two mark questions and solutions are very useful in IPE examinations.
These notes cover all the topics covered in the intermediate First-year Maths syllabus and include plenty of solutions to help you solve all the major types of Math problems asked in the IPE examinations.
The Plane
Question 1
Find the equation of the plane if the foot of the perpendicular from the origin to the plane is (2, 3, – 5).
Sol:
The plane passes through A and is perpendicular to OA, then the line segment OA is normal to the plane.
Dr’s of OA = (2, 3, – 5)
The equation of the plane passing through the point (x1, y1, z1) and dr’s (a, b, c) is
a(x – x1) + b (y – y1) + c (z – z1) = 0
⟹ 2(x – 2) + 3 (y – 3) – 5 (z + 5) = 0
2x – 4 + 3y – 9 – 5z – 25 = 0
2x + 3y – 5z – 38 = 0
Question 2
Find the equation of the plane passing through the points (0, – 1, – 1), (4, 5, 1) and (3, 9, 4)
Sol:
The equation of the plane passing through the points (x1, y1, z1) (x2, y2, z2) (x3, y3, z3) is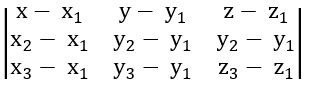
The plane passing through the points (0, – 1, – 1), (4, 5, 1) and (3, 9, 4) is
=0
⟹
= 0
x (30 – 20) – (y + 1) (20 – 6) + (z + 1) (40 – 18) = 0
x (10) – (y + 1) (14) + (z + 1) (22) = 0
10x – 14y – 14 + 22z + 22 = 0
10x – 14y + 22z + 8 = 0
2(5x – 7y + 11z + 4) = 0
∴ the equation of the plane is 5x – 7y + 11z + 4 = 0
Question 3
Find the equation to the plane parallel to the ZX-plane and passing through (0, 4, 4).
Sol:
Equation of ZX-plane is y = 0
The equation of the plane parallel to the ZX-plane is y = k
But it is passing through (0, 4, 4)
⟹ y = 4
Question 4
Find the equation to the plane passing through the point (α, β, γ) and parallel to the plane axe + by + cz + d = 0.
Sol:
The equation of the plane parallel to the plane ax + by + cz + d = 0 is ax + by + cz + k = 0
But it is passing through the point (α, β, γ)
a α + b β + c γ + k = 0
⟹ k = – a α – b β – c γ
The equation of the plane is ax + by + cz – a α – b β – c γ = 0
⟹ a(x – α) + b (y – β)+ c (z – γ) = 0
Question 5
Find the angle between the planes 2x – y + z = 6 and x + y + 2z = 7.
Sol: If θ is the angle between the planes a1 x + b1 y + c1 z + d1 = 0 and a2x + b2 y + c2 z + d2 = 0, then cos θ =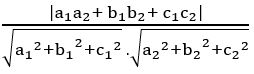 
Cos θ = 
=
=
Cos θ = cos 600
θ = 600 =
Question 6
Reduce the equation x + 2y – 2z – 9 = 0 to the normal form and hence find the dc’s of the normal to the plane.
Sol: Given plane is x + 2y – 2z – 9 = 0
x + 2y – 2z = 9
dividing into both sides by
the normal form is 
dc’s of the normal to the plane are
Question 7
Suppose a plane makes intercepts 2, 3, 4 on X, Y, Z axes respectively. Find the equation of the plane in the intercept form.
Sol: Given a = 2, b = 3, c = 4
The equation of the line in the intercept form is
⟹
Question 8
Express x – 3y + 2z = 9 in the intercept form
Sol: Given plane is x – 3y + 2z = 9
⟹ 
⟹ 
It is in the form of
a = 9, b = – 3, c = 9/2
Question 9
Find the direction cosine of the normal to the plane x + 2y + 2z – 4 = 0.
Sol: Given plane is x + 2y + 2z – 4 = 0
We know that Dr’s of the normal to the plane ax + by + cz + d = 0 are (a, b, c)
⟹ dc’s of the normal to the plane =
⟹ dr’s of the normal to the plane x + 2y + 2z – 4 = 0 are (1, 2, 2)
⟹ dc’s of the normal to the plane are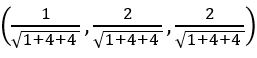 
=
Question 10
Find the midpoint of the line joining the points (1, 2, 3) and (–2, 4, 2)
Sol: Given points are A (1, 2, 3), B (–2, 4, 2)
The midpoint of AB =
=
=
Visit my Youtube Channel: Click on Below Logo
