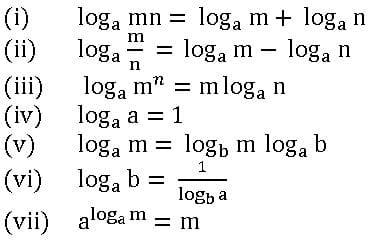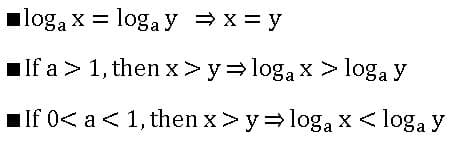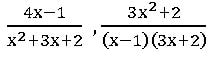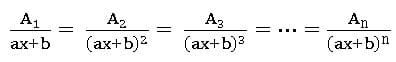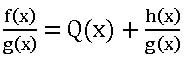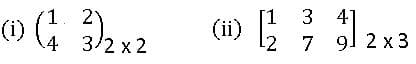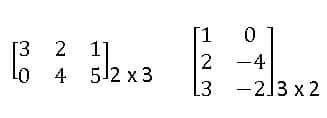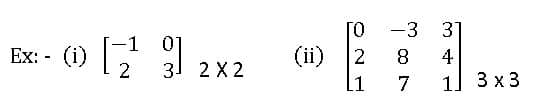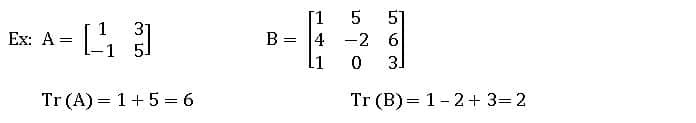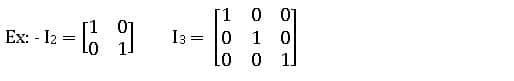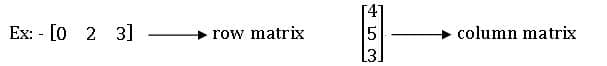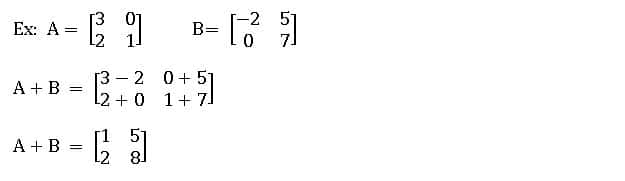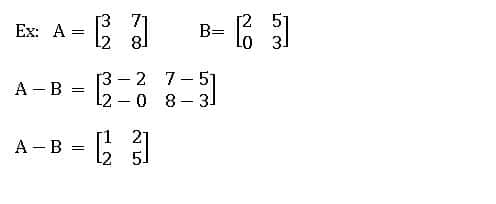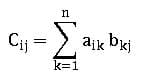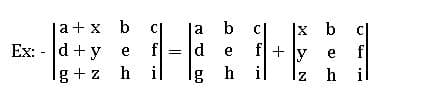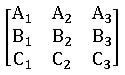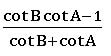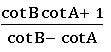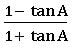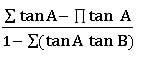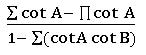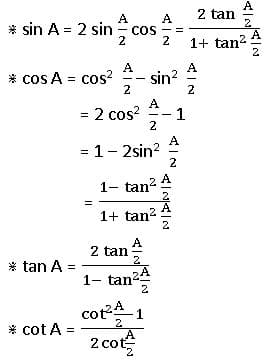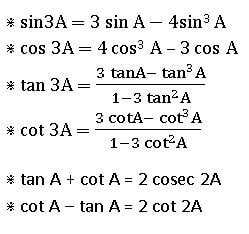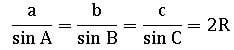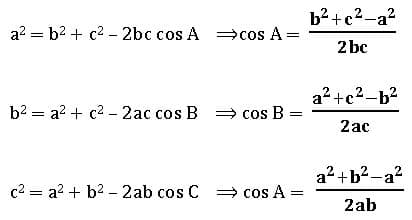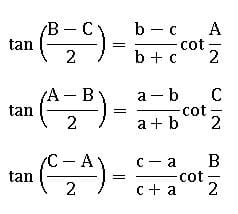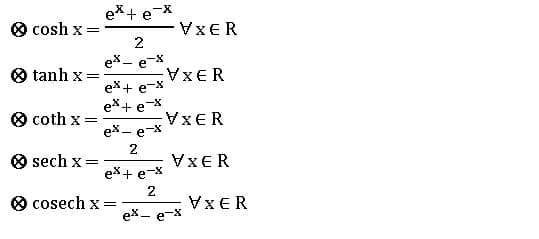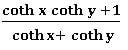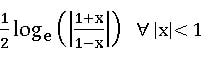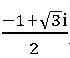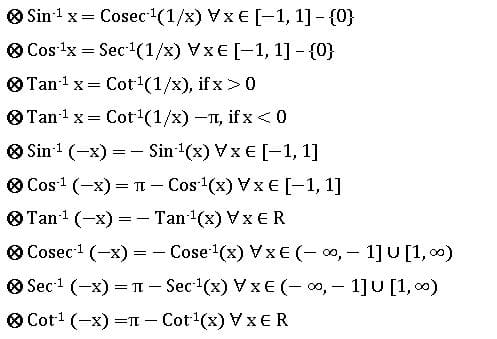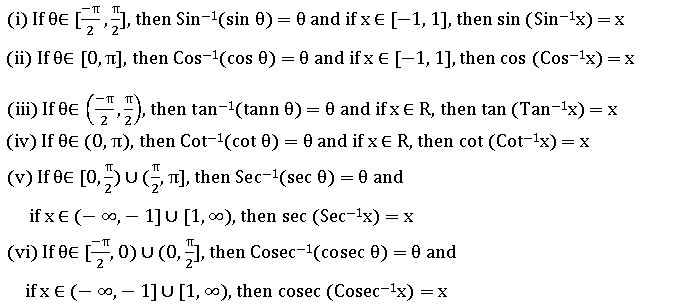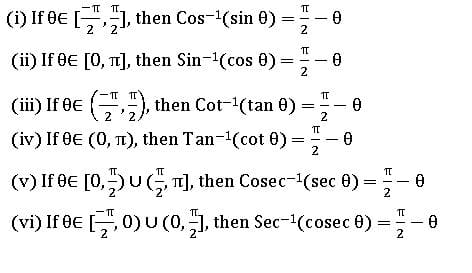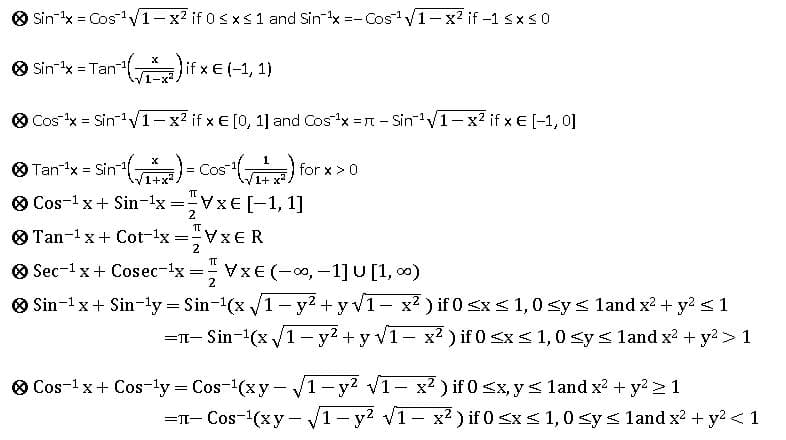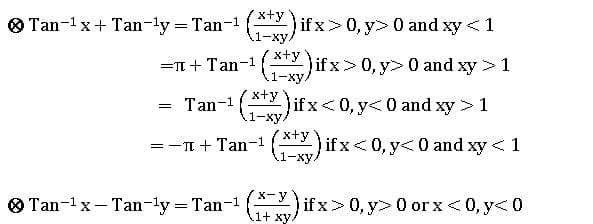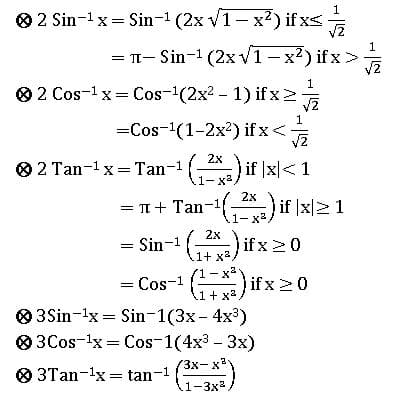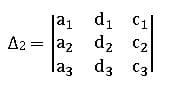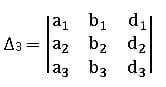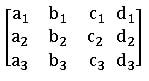Polytechnic Sem 1 – Engineering Mathematics
Polytechnic Sem 1 – Notes for Polytechnic SEM – 1 is Designed by the ” Basics in Maths” team. Here we can learn Concepts in Basic Engineering mathematics at Polytechnic Sem – I.
This Material is very Useful for Basic Engineering Mathematics Polytechnic Sem – I Students.
By learning These Notes, Basic Engineering Mathematics Polytechnic Sem – I Students can Write their Exam successfully and fearlessly.
LOGARITHMS
Logarithm: For ant two positive real numbers a, b, and a ≠ 1. If the real number x such then ax = b, then x is called logarithm of b to the base a. it is denoted by ![]()
 Standard formulae of logarithms:
Standard formulae of logarithms:
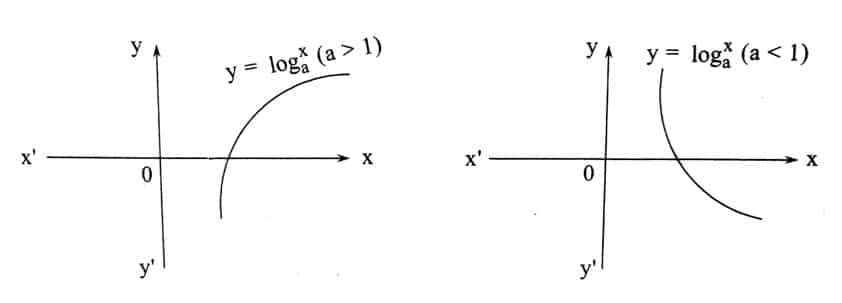
Logarithmic Function:
Let a be a positive real number and a ≠ 1. The function f: (o, ∞) → R Defined by f(x) = ![]()
PARTIAL FRACTIONS
Fractions:
If f(x) and g(x) are two polynomials, g(x) ≠ 0, then ![]() is called rational fraction.
is called rational fraction.
Ex:
Proper Fraction:
A rational fraction![]() is said to be a Proper fraction if the degree of g(x) is greater than the degree of f(x).
is said to be a Proper fraction if the degree of g(x) is greater than the degree of f(x).
Ex:
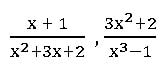 etc. are the proper fractions.
etc. are the proper fractions.
Improper Fraction:
A rational fraction![]() is said to be an Improper fraction if the degree of g(x) is less than the degree of f(x).
is said to be an Improper fraction if the degree of g(x) is less than the degree of f(x).
Ex:
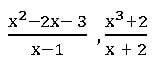 etc. are the Improper fractions.
etc. are the Improper fractions.
Partial Fractions:
Expressing rational fractions as the sum of two or more simpler fractions is called resolving a given fraction into a partial fraction.
∎ If R(x) =![]() is proper fraction, then
is proper fraction, then
Case(i): – For every factor of g(x) of the form (ax + b) n, there will be a sum of n partial fractions of the form:
Case(ii): – For every factor of g(x) of the form (ax2 + bx + c) n, there will be a sum of n partial fractions of the form:
∎ If R(x) =![]() is improper fraction, then
is improper fraction, then
Case (i): – If degree f(x) = degree of g(x),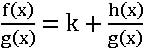 where k is the quotient of the highest degree term of f(x) and g(x).
where k is the quotient of the highest degree term of f(x) and g(x).
Case (ii): – If f(x) > g(x)
MATRICES AND DETERMINANTS
Matrix: A set of numbers arranged in the form of a rectangular array having rows and columns is called Matrix.
•Matrices are generally enclosed by brackets like
•Matrices are denoted by capital letters A, B, C, and so on
•Elements in a matrix are real or complex numbers; real or complex real-valued functions.
Oder of Matrix: A matrix having ‘m’ rows and ‘n’ columns is said to be of order m x n read as m by n.
Ex:
Types Of Matrices
Rectangular Matrix: A matrix in which the no. of rows is not equal to the no. of columns is called a rectangular matrix.
Square Matrix: A matrix in which the no. of rows is equal to no. of columns is called a square matrix.
Principal diagonal (diagonal) Matrix: If A = [a ij] is a square matrix of order ‘n’ the elements a11, a22, a33, ………. An n is said to constitute its principal diagonal.
Trace Matrix: The sum of the elements of the principal diagonal of a square matrix A is called the trace of the matrix. It is denoted by Tr (A).
Diagonal Matrix: If each non-diagonal element of a square matrix is ‘zero’ then the matrix is called a diagonal matrix.
Scalar Matrix: If each non-diagonal element of a square matrix is ‘zero’ and all diagonal elements are equal to each other, then it is called a scalar matrix.
Identity Matrix or Unit Matrix: If each of the non-diagonal elements of a square matrix is ‘zero’ and all diagonal elements are equal to ‘1’, then that matrix is called unit matrix
Null Matrix or Zero Matrix: If each element of a matrix is zero, then it is called a null matrix.
Row matrix & column Matrix: A matrix with only one row s called a row matrix and a matrix with only one column is called a column matrix.
Triangular matrices:
A square matrix A = [aij] is said to be upper triangular if aij = 0 ∀ i > j
A square matrix A = [aij] is said to be lower triangular matrix aij = 0 ∀ i < j
Equality of matrices:
matrices A and B are said to be equal if A and B are of the same order and the corresponding elements of A and B are equal.

Addition of matrices:
If A and B are two matrices of the same order, then the matrix obtained by adding the corresponding elements of A and B is called the sum of A and B. It is denoted by A + B.
Subtraction of matrices:
If A and B are two matrices of the same order, then the matrix obtained by subtracting the corresponding elements of A and B is called the difference from A to B.
Product of Matrices:
Let A = [aik]mxn and B = [bkj]nxp be two matrices, then the matrix C = [cij]mxp where
Note: Matrix multiplication of two matrices is possible when no. of columns of the first matrix is equal to no. of rows of the second matrix.
A m x n . Bp x q = AB mx q; n = p
Transpose of Matrix: If A = [aij] is an m x n matrix, then the matrix obtained by interchanging the rows and columns is called the transpose of A. It is denoted by AI or AT.
Note: (i) (AI)I = A (ii) (k AI) = k . AI (iii) (A + B )T = AT + BT (iv) (AB)T = BTAT
Symmetric Matrix: A square matrix A is said to be symmetric if AT =A
If A is a symmetric matrix, then A + AT is symmetric.
Skew-Symmetric Matrix: A square matrix A is said to be skew-symmetric if AT = -A
If A is a skew-symmetric matrix, then A – AT is skew-symmetric.
Minor of an element: Consider a square matrix 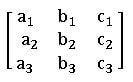
the minor element in this matrix is defined as the determinant of the 2×2 matrix obtained after deleting the rows and the columns in which the element is present.
Ex: – minor of a3 is  = b1c2 – b2c1
= b1c2 – b2c1
Cofactor of an element: The cofactor of an element in i th row and j th column of A3×3 matrix is defined as its minor multiplied by (- 1) i+j.
Properties of determinants:
If each element of a row (column) f a square matrix is zero, then the determinant of that matrix is zero.
If A is a square matrix of order 3 and k is scalar then.
If two rows (columns) of a square matrix are identical (same), then Det. Of that matrix is zero.
If each element in a row (column) of a square matrix is the sum of two numbers then its determinant can be expressed as the sum of the determinants.
If each element of a square matrix are polynomials in x and its determinant is zero when x = a, then (x-a) is a factor of that matrix.
For any square matrix A Det(A) = Det (AI).
Det (AB) = Det(A). Det(B).
For any positive integer n Det (An) = (DetA)n.
Singular and non-singular matrices:
A Square matrix is said to be singular if its determinant is is zero, otherwise it is said to be non-singular matrix.
∴ A is singular matrix
Det(B) = 4 + 4 = 8≠ 0
∴ B is non-singular
Adjoint of a matrix: The transpose of the matrix formed by replacing the elements of a square matrix A with the corresponding cofactors is called the adjoint of A.
Let A =  and cofactor matrix of A =
and cofactor matrix of A = 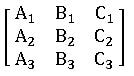
Invertible matrix: Let A be a square matrix, we say that A is invertible if there exists a matrix B such that AB =BA = I, where I is a unit matrix of the same order as A and B.
Compound Angles
The algebraic sum of two or more angles is called a ‘compound angle’. Thus, angles A + B, A – B, A + B + C etc., are Compound Angles
For any two real numbers A and B
⋇ sin (A + B) = sin A cos B + cos A Cos B
⋇ sin (A − B) = sin A cos B − cos A Cos B
⋇ cos (A + B) = cos A cos B − sin A sin B
⋇ cos (A − B) = cos A cos B + sin A sin B
⋇ sin (A + B + C) = ∑sin A cos B cos C − sin A sin B sin C
⋇ cos (A + B + C) = cos A cos B cos C− ∑cos A sin B sin C
⋇ sin (A + B) sin (A – B) = sin2 A – sin2 B = cos2 B – cos2 A
⋇ cos (A + B) cos (A – B) = cos2 A – sin2 B = cos2 B – sin2 A
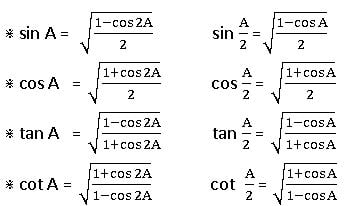
Multiple and Sub Multiple Angles
If A is an angle, then its integral multiples 2A, 3A, 4A, … are called ‘multiple angles ‘of A and the multiple of A by fraction like are called ‘submultiple angles.
∎ If ![]() is not an add multiple of
is not an add multiple of ![]()
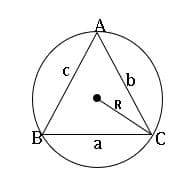
PROPERTIES OF TRIANGLES
In ∆ABC,
Lengths AB = c; BC = a; AC =b
The area of the triangle is denoted by ∆.
Perimeter of the triangle = 2s = a + b + c
A = ∠CAB; B = ∠ABC; C = ∠BCA.
R is circumradius.
Sine rule:
In ∆ABC,
⟹ a = 2R sin A; b = 2R sin B; c = 2R sin C
Where R is the circumradius and a, b, c, are lengths of the sides of ∆ABC.
Cosine rule:
In ∆ABC,
Projection rule:
In ∆ABC,
a = b cos C + c cos B
b = a cos C + c cos A
c = a cos B + b cos A
Tangent rule (Napier’s analogy):
Area of the triangle:
In ∆ABC, a, b, and c are sides
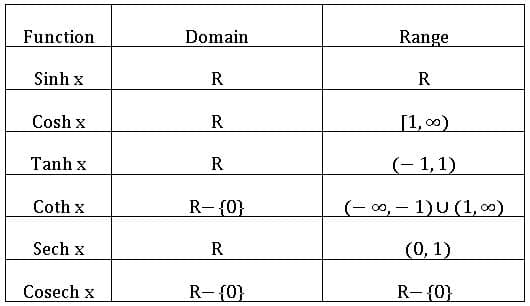
HYPERBOLIC FUNCTIONS
⨂ The function f: R→R defined by f(x) =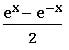 ∀ x ∈ R is called the ‘hyperbolic sin’ function. It is denoted by Sinh x.
∀ x ∈ R is called the ‘hyperbolic sin’ function. It is denoted by Sinh x.
Similarly,
Identities:
⨂ cosh2x – sinh2 x = 1
cosh2x = 1 + sinh2 x
sinh2 x = cosh2 x – 1
⨂ sech2 x = 1 – tanh2 x
tanh2 x = 1 – sesh2 x
⨂ cosech2 x = coth2 x – 1
coth2 x = 1 + coth2 x
Addition formulas of hyperbolic functions:
⨂ Sinh (x + y) = Sinh x Cosh y + Cosh x Sinh y
⨂ Sinh (x − y) = Sinh x Cosh y − Cosh x Sinh y
⨂ Cosh (x + y) = Cosh x Cosh y + Sinh x Sinh y
⨂ Cosh (x − y) = Cosh x Cosh y − Sinh x Sinh y
⨂ sinh 2x = 2 sinh x cosh 2x =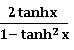
⨂ cosh 2x = cosh2x + sinh2 x = 2 cosh2x – 1 = 1 + 2 sinh2x =![]()
Inverse hyperbolic functions:
COMPLEX NUMBERS
The equation x2 + 1 = 0 has no roots in real number system.
∴ scientists imagined a number ‘i’ such that i2 = − 1.
Complex number:
if x, y are any two real numbers then the general form of the complex number is
z = x + i y; where x real part and y is the imaginary part.
3 + 4i, 2 – 5i, – 3 + 2i are the examples for Complex numbers.
- z = x +i y can be written as (x, y).
- If z1 = x1 + i y1, z2 = x2 + i y2, then
- z1 + z2 = (x1 + x2, y1 + y2) = (x1 + x2) + i (y1 + y2)
- z1 − z2 = (x1 − x2, y1 − y2) = (x1 − x2) + i (y1 − y2)
- z1∙ z2 = (x1 x2 −y1 y2, x1y2 + x2y1) = (x1x2 −y1 y2) + i (x1y2 +x2 y1)
- z1/ z2 = (x1x2 + y1 y2/x22 +y22, x2 y1 – x1y2/ x22 +y22)
= (x1x2 + y1 y2/x22 +y22) + i (x2 y1 – x1y2/ x22 +y22)
Multiplicative inverse of complex number:
The multiplicative inverse of the complex number z is 1/z.
z = x + i y then 1/z = x – i y/ x2 + y2
Conjugate complex numbers:
The complex numbers x + i y, x – i y are called conjugate complex numbers.
The sum and product of two conjugate complex numbers are real.
If z1, z2 are two complex numbers then
Modulus and amplitude of complex numbers:
Modulus: – If z = x + i y, then the non-negative real number![]() is called modulus of z and it is denoted by
is called modulus of z and it is denoted by![]() or ‘r’.
or ‘r’.
Amplitude: – The complex number z = x + i y represented by the point P (x, y) on the XOY plane. ∠XOP = θ is called amplitude of z or argument of z.
x = r cos θ, y = r sin θ
x2 + y2 = r2 cos2θ + r2 sin2θ = r2 (cos2θ + sin2θ) = r2(1)
⇒ x2 + y2 = r2
• Arg (z) = tan−1(y/x)
• Arg (z1.z2) = Arg (z1) + Arg (z2) + nπ for some n ∈ { −1, 0, 1}
• Arg(z1/z2) = Arg (z1) − Arg (z2) + nπ for some n ∈ { −1, 0, 1}
Note:
∎ eiθ = cos θ + i sin θ
∎ e−iθ = cos θ − i sin θ
De-Moiver’s theorem
For any integer n and real number θ, (cos θ + i sin θ) n = cos n θ + i sin n θ.
→ cos α + i sin α can be written as cis α
→ cis α.cis β= cis (α + β)
→ 1/cisα = cis(-α)
→ cisα/cisβ = cis (α – β)
⟹ (cos θ + i sin θ) -n = cos n θ – i sin n θ
⟹ (cos θ + i sin θ) (cos θ – i sin θ) = cos2θ – i2 sin2θ = cos2θ + sin2θ = 1.
→ cos θ + i sin θ = 1/ cos θ – i sin θ and cos θ – i sin θ = 1/ cos θ + i sin θ
⟹ (cos θ – i sin θ) n = (1/ (cos θ –+i sin θ)) n = (cos θ + i sin θ)-n = cos n θ – i sin n θ
nth root of a complex number: let n be a positive integer and z0 ≠ 0 be a given complex number. Any complex number z satisfying z n = z0 is called an nth root of z0. It is denoted by z01/n or![]()
⟹ let z = r (cos θ + i sin θ) ≠ 0 and n be a positive integer. For k∈ {0, 1, 2, 3…, (n – 1)}
let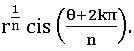 Then a0, a1, a2, …, an-1 are all n distinct nth roots of z and any nth root of z is coincided with one of them.
Then a0, a1, a2, …, an-1 are all n distinct nth roots of z and any nth root of z is coincided with one of them.
nth root of unity: Let n be a positive integer greater than 1 and![]()
Note:
- The sum of the nth roots of unity is zero.
- The product of nth roots of unity is (– 1) n – 1.
- The nth roots of unity 1, ω, ω2, …, ωn-1 are in geometric progression with common ratio ω.
Cube root of unity:
x3 – 1 = 0 ⇒ x3 = 1
x =11/3
ω2 +ω + 1 = 0 and ω3 = 1
TRANSFORMATIONS
For A, B∈ R
⋇ sin (A + B) + sin (A – B) = 2sin A cos B
⋇ sin (A + B) −sin (A – B) = 2cos A sin B
⋇ cos (A + B) + cos (A – B) = 2 cos A cos B
⋇ cos (A + B) − cos (A – B) = − 2sin A sin B
For any two real numbers C and D
If A + B + C = π or 1800, then
⋇ sin (A + B) = sin C; sin (B + C) = sin A; sin (A + C) = sin B
⋇ cos (A + B) = − cos C; cos (B + C) = −cos A; cos (A + C) = − cos B
⋇ sin![]() = cos
= cos![]() ; sin
; sin![]() = cos
= cos![]() ; sin
; sin![]() = cos
= cos![]()
⋇ cos ![]() = sin
= sin![]() ; cos
; cos![]() = sin
= sin![]() ; cos
; cos![]() = sin
= sin![]()
⋇ sin (A + B) = cos C; sin (B + C) = cos A; sin (A + C) = cos B
⋇ cos (A + B) = sin C; cos (B + C) = sin A; cos (A + C) = sin B
Polytechnic Sem 1
INVERSE TRIGONOMETRIC RATIOS
If A, B are two sets and f: A→ B is a bijection, then f-1 is existing and f-1: B → A is an inverse function.
Properties of Inverse Trigonometric functions:
Engineering Mathematics
Solutions of Simultaneous Equations
Matrix Inversion Method:
Let a system of simultaneous equations be
a1 x + b1 y + c1z = d1
a2 x + b2 y + c2z = d2
a3 x + b3 y + c3z = d3
The matrix form of the above equations is
Therefore, the matrix equation is AX = B
If Det A ≠ 0, A-1 is exists
X = A-1 B
By using above Condition, we get the values of x, y and z
This method is called as Matrix Inversion Method
Cramer’s Method:
Let a system of simultaneous equations be
a1 x + b1 y + c1z = d1
a2 x + b2 y + c2z = d2
a3 x + b3 y + c3z = d3
∆1 is obtained by replacing the coefficients of x (1st column elements of ∆) by constant values
∆2 is obtained by replacing the coefficients of y (2nd column elements of ∆) by constant values
∆3 is obtained by replacing the coefficients of z (3rd column elements of ∆) by constant values
This method is called Cramer’s Method
Gauss-Jordan Method:
Let a system of simultaneous equations be
a1 x + b1 y + c1z = d1
a2 x + b2 y + c2z = d2
a3 x + b3 y + c3z = d3
Augmented matrix: The coefficient matrix (A) augmented with the constant column matrix (B) is called the augmented matrix. It is denoted by [AD].
This Matrix is reduced to the standard form of by using row operations
by using row operations
- Interchanging any two rows
- Multiplying the elements of any two elements by a constant.
- Adding to the elements of one row with the corresponding elements of another row multiplied by a constant.
∴ The solution of a given system of simultaneous equations is x = α, y = β, and z = γ.
Procedure to get the standard form:
- Take the coefficient of x as the unity as a first equation.
- If 1 is there in the first-row first column, then make the remaining two elements in the first column zero.
- After that, if one element in R2 or R3 is 1, then make the remaining two elements in that column C2 or C3 as zeroes.
- If any row contains two elements as zeros and only non-zero divide that row elements with the non-zero element to get unity and make the remaining two elements in that column as zeros.
Engineering Mathematics
PDF FILE: Mathematics Notes 4 Polytechnic SEM – I