Functions Exercise 1a Solutions
Functions Exercise 1a
The famous mathematician ” Lejeune Dirichlet” defined a function.
Function: A variable is a symbol which represents any one of a set of numbers, if two variables x and y so related that whenever a value is assigned to x there is autometically assigned by some rule or correspondence a value to y, then we say y is a function of x.
Chapter 1 Functions Exercise 1a Solutions for inter first year students, prepared by Mathematics expert of www.basicsinmaths.com
Exercise 1a
I.
1. If the function f is defined by
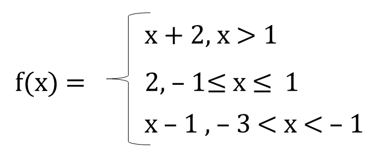
then find the values of (i) f (3) (ii) f (0) (iii) f (– 1.5) (iv) f (2) + f (– 2) (v) f (– 5 )
Sol:
Given 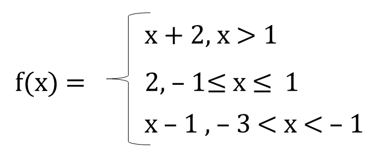
Domain of f(x) is (– 3, ∞)
(i) f (3)
3 lies in the interval x > 1
⟹ f(x) = x + 2
f(3) = 3 + 2 = 5
∴ f (3) = 5
(ii) f (0)
0 lies in interval – 1 ≤ x ≤ 1
⟹f(x) = 2
∴ f (0) = 2
(iii) f (– 1.5)
– 1.5 lies in interval – 3 < x < – 1
⟹f(x) = x – 1
f (– 1.5) = – 1.5 – 1 = – 2.5
∴ f (– 1.5) = – 2.5
(iv) f (2) + f (– 2)
2 lies in the interval x > 1
⟹ f (x) = x + 2
f (3) = 2 + 2 = 4
f (2) = 4
– 2 lies in interval – 3 < x < – 1
⟹f(x) = x – 1
f (– 2) = – 2 – 1 = – 3
f (– 2) = – 2 – 1 = – 3
now f (2) + f (– 2) = 4 – 3 = 1
∴ f (2) + f (– 2) = 1
(v) f (– 5)
since domain of f(x) is (– 3, ∞)
f (– 5) is not defined
2. If f: R – {0} ⟶ R is defined by f(x) =  , then show that f (x) + f (1/x) = 0
, then show that f (x) + f (1/x) = 0
Sol:
Given f: R – {0} ⟶ R is defined by f(x) = 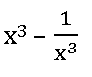
f (1/x) = 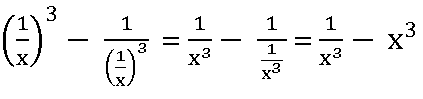
Now
f (x) + f (1/x) = 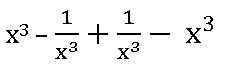
∴ f (x) + f (1/x) = 0
3. If f: R ⟶ R is defined by f(x) =  , then show that f (tan θ) = cos 2θ
, then show that f (tan θ) = cos 2θ
Sol:
Given f: R ⟶ R is defined by f(x) =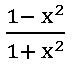
f (tan θ) =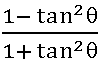
= cos 2θ 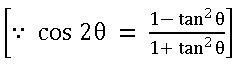
4. If f: R – {±1} ⟶ R is defined by f(x) =  , then show that f
, then show that f  = 2 f (x)
= 2 f (x)
Sol:
Given f: R – {±1} ⟶ R is defined by f(x) =
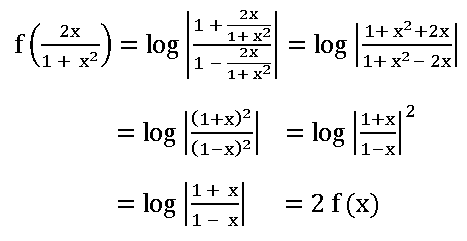
5. If A = {– 2, – 1, 0, 1, 2} and f: A ⟶ B is a surjection (onto function) defined by f(x) = x2 + x + 1, then find B
Sol:
Given A = {– 2, – 1, 0, 1, 2} and f: A ⟶ B is a surjection defined by f(x) = x2 + x + 1
f(– 2) = (–2)2 + (–2) + 1
= 4 – 2 + 1 = 3
f(– 1) = (–1)2 + (–1) + 1
= 1 – 1 + 1 = 1
f(0) = (0)2 + (0) + 1
= 0 + 0 + 1 = 1
f(1) = (1)2 + (1) + 1
=1 +1 + 1 = 3
f( 2) = (2)2 + (2) + 1
= 4 + 2 + 1 = 4
∴ B = {1, 3, 7}
Functions Exercise 1a
6. If A = {1, 2, 3,4} and f: A ⟶ B is a surjection defined by f(x) =  , then find range of f.
, then find range of f.
Sol:
Given A = {1, 2, 3,4} and f: A ⟶ B is a surjection defined by f(x) =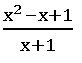
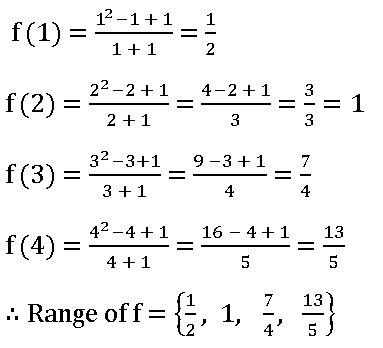
7. If f (x + y) = f (xy) ∀ x, y ∈ R, then prove that f is a constant function
Sol:
Given f (x + y) = f (xy) ∀ x, y ∈ R
Let x = 0 and y = 0
f (0 + 0) = f (0 × 0) = f (0)
f (1) = f (0 + 1)
= f (0 × 1)
= f (0)
f (2) = f (1 + 1)
= f (1 × 1)
= f (1)
= f (0)
f (3) = f (1 + 2)
= f (1 × 2)
= f (2)
= f(0)
Similarly, f(4) = 0
f(5) = 0
and so on.
∴ f is a constant function
PDF Files || Inter Maths 1A &1B || (New)
6th maths notes|| TS 6 th class Maths Concept
II.
1. If A = {x/ – 1 ≤ x ≤ 1}, f(x) = x2, g(x) = x3, which of the following are surjections?
(i) f: A ⟶ A (ii) g: A ⟶ A
Sol:
(i) Given A = {x/ – 1 ≤ x ≤ 1}, f(x) = x2
A = {– 1, 0, 1}; f: A ⟶ A
f (x) = x2
f (– 1) = (– 1)2 = 1
f (0) = (0)2 = 0
f (1) = (1)2 = 1
∵ range is not equal to co domain of f
f is nor a surjection
(ii) A = {x/ – 1 ≤ x ≤ 1}, g (x) = x3
A = {– 1, 0, 1}; g: A ⟶ A
g (x) = x3
g (– 1) = (– 1)3 = – 1
g (0) = (0)3 = 0
g (1) = (1)3 = 1
∵ range is equal to co domain of f
f is a surjection
2. Which if the following are injection, surjection or bijection? Justify your answer
(i) f: R ⟶ R defined by f(x) =
let x1, x2 ∈ R
f(x1) = f(x2)
![]()
2x1 + 1 = 2x2 + 1
2x1 = 2x2
x1 = x2
x1, x2 ∈ R, f(x1) = f(x2) ⟹ x1 = x2
∴ f is an injection
Let y = f(x)
y =![]()
3y = 2x + 1
3y – 1 = 2x
⟹ x = ![]() ∈ R
∈ R
Now
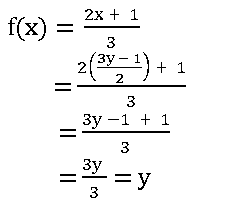
∴ f is surjection
f is injection and surjection
∴ f is a bijection
(ii) f: R ⟶ (0, ∞) defined by f(x) = 2x
let x1, x2 ∈ R
f(x1) = f(x2)
![]()
x1 = x2
x1, x2 ∈ R, f(x1) = f(x2) ⟹ x1 = x2
∴ f is an injection
Let y = f(x)
y = 2x
x = ![]() ∈ (0, ∞)
∈ (0, ∞)
Now f(x) = 2x
= ![]()
= y
∴ f is surjection
f is injection and surjection
∴ f is a bijection
(iii) f: (0, ∞) ⟶ R defined by f(x) =
let x1, x2 ∈ (0, ∞)
f(x1) = f(x2)
![]()
x1 = x2
x1, x2 ∈ (0, ∞), f(x1) = f(x2) ⟹ x1 = x2
∴ f is an injection
Let y = f(x)
y =![]()
x = ey ∈ (0, ∞)
Now f(x) =![]()
= ![]()
= y
∴ f is surjection
f is injection and surjection
∴ f is a bijection
(iv) f: [0, ∞) ⟶ [0, ∞) defined by f(x) = x2
let x1, x2 ∈ [0, ∞)
f(x1) = f(x2)
![]()
x1 = x2 [∵ x1, x2 ∈ [0, ∞)]
x1, x2 ∈ [0, ∞), f(x1) = f(x2) ⟹ x1 = x2
∴ f is an injection
Let y = f(x)
y = x2
x = ![]() ∈ [0, ∞)
∈ [0, ∞)
Now f(x) = x2
=![]()
= y
∴ f is surjection
f is injection and surjection
∴ f is a bijection
(v) f: R ⟶ [0, ∞) defined by f(x) = x2
let x1, x2 ∈ R
f(x1) = f(x2)
![]()
x1 = ± x2 [∵ x1, x2 ∈ R]
x1, x2 ∈ [0, ∞), f(x1) = f(x2) ⟹ x1 ≠ x2
∴ f is not an injection
Let y = f(x)
y = x2
x = ![]() ∈ R
∈ R
Now f(x) = x2
=![]()
= y
∴ f is surjection
f is not an injection but surjection
∴ f is not a bijection
(vi) f: R ⟶ R defined by f(x) = x2
let x1, x2 ∈ R
f(x1) = f(x2)
x1 = ± x2 [∵ x1, x2 ∈ R]
x1, x2 ∈ [0, ∞), f(x1) = f(x2) ⟹ x1 ≠ x2
∴ f is not an injection
f (1) = 12 = 1
f (– 1) = (–1)2 = 1
here ‘– 1’ has no pre image
∴ f is not a surjection
f is not an injection and not surjection
∴ f is not a bijection
hai
3. Is g = {(1, 1), (2, 3), (3, 5), (4, 7)} is a function from A = {1, 2, 3, 4} to B = {1, 3, 5, 7}? If this is given by the formula g(x) = ax + b, then find a and b
Sol:
Given A = {1, 2, 3, 4}, B = {1, 3, 5, 7} and g = {(1, 1), (2, 3), (3, 5), (4, 7)}
g (1) = 1; g(2) = 3; g(3) = 5 ; g(4) = 7
here, every element of set A has a unique image in set B
∴ g: A ⟶ B is a function
And also given g(x) = ax + b
g (1) = 1
⟹ a (1) + b = 1
a + b = 1
b = 1 – a _______________ (1)
g (2) = 3
a (2) + b = 3
2a + b = 3
2a + 1 – a = 3 (from (1))
a+ 1 = 3
a = 2
b = 1 – 2
b = – 1
∴ a = 2, b = – 1
4. If the function f: R ⟶ R defined by f(x) =  , then show that f (x + y) + f (x – y) = 2 f (x) f (y).
, then show that f (x + y) + f (x – y) = 2 f (x) f (y).
Sol:
Given the function f: R ⟶ R defined by f(x) =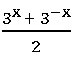
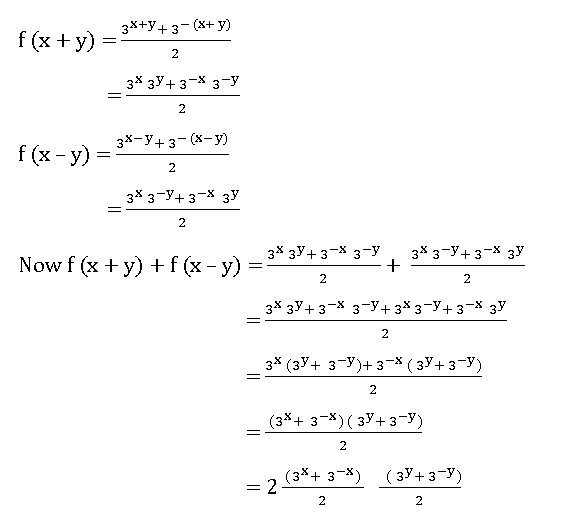
= 2 f (x) f (y)
5. If the function f: R ⟶ R defined by f(x) = 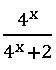 , then show that f (1 – x) = 1 – f (x)
, then show that f (1 – x) = 1 – f (x)
and hence reduce the value of 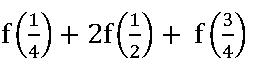
Sol:
Given the function f: R ⟶ R defined by f(x) =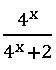
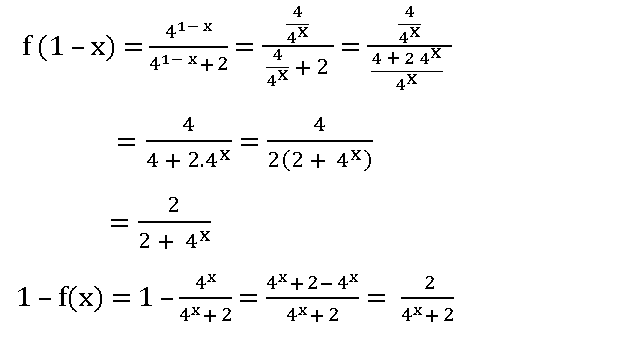
∴ f (1 – x) = 1 – f(x)
TS 10th Class Maths Concept (T/M)
TS 10th class maths concept (E/M)
6. If the function f: {– 1, 1} ⟶ {0, 2}, defined by f(x) = ax + b is a surjection, then find a and b
Sol:
Given the function f: {– 1, 1} ⟶ {0, 2}, defined by f(x) = ax + b is a surjection
Case(i)
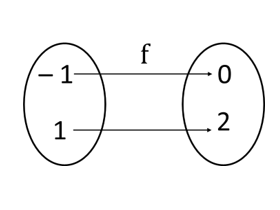
If f(– 1) = 0 and f(1) = 2
a (– 1) + b = 0
– a + b = 0
b = a ————(1)
and
a (1) + b = 2
a + b = 2
a + a = 2 [ from (1)]
2a = 2
a = 1
b = 1
Case (ii)
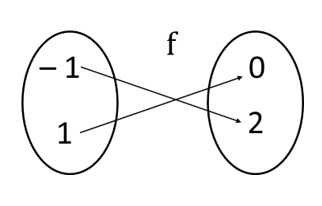
If f(– 1) = 2 and f(1) = 0
a (– 1) + b = 2
– a + b =
b = 2 + a ————(2)
and
a (1) + b = 0
a + b = 0
a + 2 + a = 0 [ from (2)]
2a + 2 = 0
2a = – 2
a = – 1
b = 1
From Case(i) and Case (ii) a = ±1 and b = 1
7. If f(x) = cos (log x), then show that  = 0
= 0
Sol
Given f(x) = cos (log x)

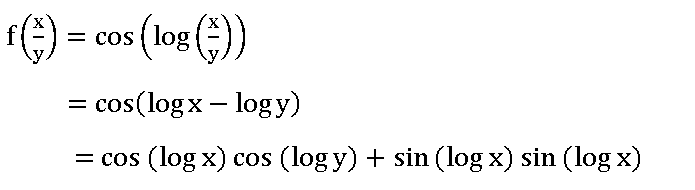
 =
=
cos (log x) cos (log y) – ![]() [cos (log x) cos (log y) – sin (log x) sin (log x)
[cos (log x) cos (log y) – sin (log x) sin (log x)
+ cos (log x) cos (log y) + sin (log x) sin (log x)]
= cos (log x) cos (log y) – ![]() [2cos (log x) cos (log y)]
[2cos (log x) cos (log y)]
= cos (log x) cos (log y) – cos (log x) cos (log y)
∴ 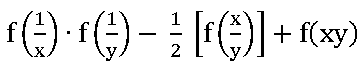 = 0
= 0
Visit my Youtube Channel: Click on Below Logo


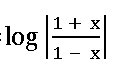 , then show that f
, then show that f 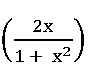 = 2 f (x)
= 2 f (x)

