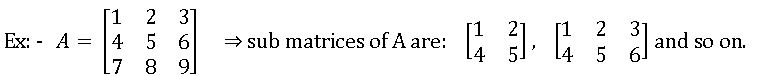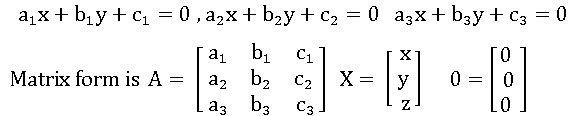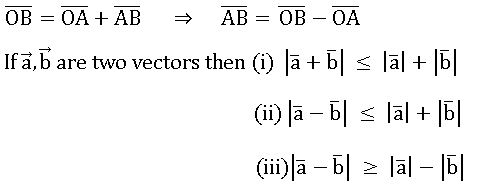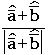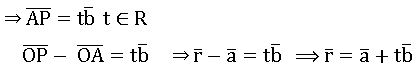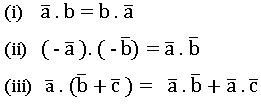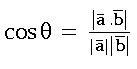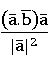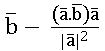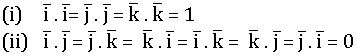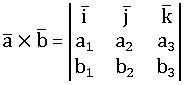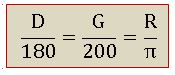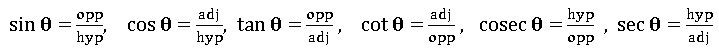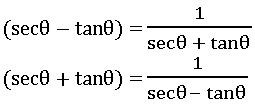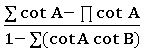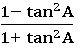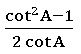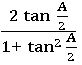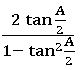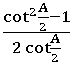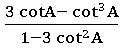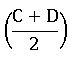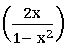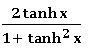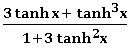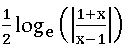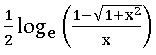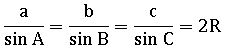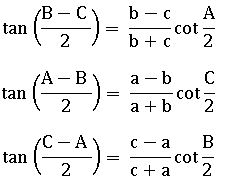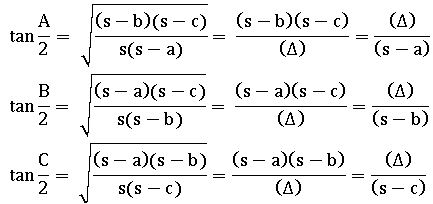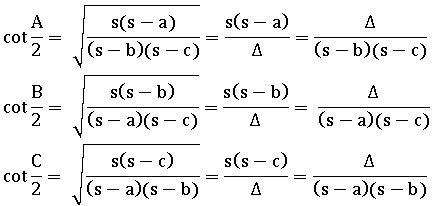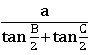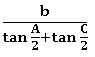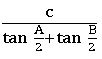Maths ia Concept
Maths ia Concept

Maths ia Concept designed by the ‘Basics in Maths’ team. These notes to do help the TS intermediate first-year Math students fall in love with mathematics and overcome the fear.
These notes cover all the topics covered in the TS I.P.E first-year maths 1A syllabus and include plenty of formulae and concepts to help you solve all the types of Inter Math problems asked in the I.P.E and entrance examinations.
1.Functions
Set: A collection of well-defined objects is called a set.
Ordered pair: Two elements a and b listed in a specific order form. An ordered pair denoted by (a, b).
Cartesian product: Let A and B are two non-empty sets. The Cartesian product of A and B is denoted by A × B and is defined as a set of all ordered pairs (a, b) where a ϵ A and b ϵB
![]()
Relation: Let A and B are two non-empty sets the relation R from A to B is a subset of A×B.
⇒ R: A→B is a relation if R⊂ A × B
Function:
A relation f: A → B is said to be a function if ∀ aϵ A there exists a unique element b such that (a, b) ϵ f. (Or)
A relation f: A → B is said to be a function if
(i) x ϵ A ⇒ f(x) ϵ B
(ii) x1 , x2 ϵ A , x1 = x2 in A ⇒ f(x1) = f(x2) in B.
Note: If A, B are two finite sets then the no. of functions that can be defined from A to B is n(B)n(A)
VARIOUS TYPES OF FUNCTIONS
One– one Function (Injective):- A function f: A→ B is said to be a one-one function or injective if different elements in A have different images in B.
(Or)
A function f: A→ B is said to be one-one function if f(x1) = f(x2) in B ⇒ x1 = x2 in A.
Note: No. of one-one functions that can be defined from A into B is n(B) p n(A) if n(A) ≤ n(B)
On to Function (Surjection): – A function f: A→ B is said to be onto function or surjection if for each yϵ B ∃ x ϵ A such that f(x) =y
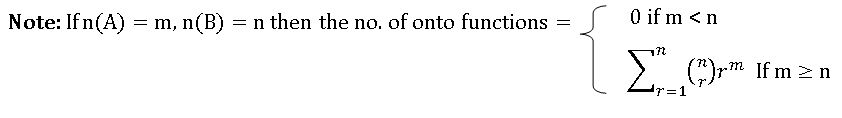
Note: if n(A) = m and n(B) = 2 then no. of onto functions = 2m – 2
Bijection: – A function f: A→ B is said to be Bijection if it is both ‘one-one and ‘onto’.

Constant function: A function f: A→ B is said to be constant function if f(x) = k ∀ xϵA
Identity function: Let A be a non-empty set, then the function defined by IA : A → A, I(x)=x is called identity function on A.
Equal function: Two functions f and g are said to be equal if
(i) They have same domain (D)
(ii) f(x) = g(x) ∀ xϵ D
Even function: A function f: A→ B is said to be even function if f (- x) = f(x) ∀ xϵ A
Odd function: A function f: A→ B is said to be odd function if f (- x) = – f(x) ∀ xϵ A
Composite function: If f: A→B, g: B→C are two functions then the composite relation is a function from A to C.
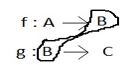
gof: A→C is a composite function and is defined by gof(x) = g(f(x)).
Step function: A number x = I + F
I → integral part = [x]
F → fractional part = {x}
∴ x = [x] + {x}
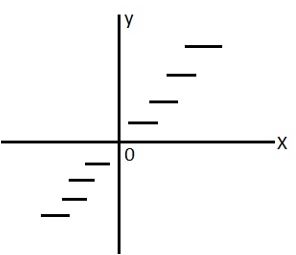 If y = [x] then domain = R and
If y = [x] then domain = R and
Range = Z
0 ≤ x ≤ 1, [x] = 0
1≤ x ≤ 2, [x] = 1
-1 ≤ x ≤ 0, [x] = -1
If k is any integer [ x + k] = k + [x]
The value of [x] is lies in x – 1 < [x] ≤ 1.
Inverse function: If f: A → B is bijection then f -1 is exists
f-1: B → A is an inverse function of f.


SOME IMPORTANT POINTS
of subsets of a set of n elements is 2n
of proper subsets of a set of n elements is 2n – 1
Let A and B are two non-empty finite sets and f: A → B is a function. This function will
One-one if n(A) ≤ n(B)
On to if n(A) ≥ n(B)
Bijection if n(A) = n(B).
2. MATHEMATICAL INDUCTION
3. MATRICES
Matrix: An ordered rectangular array of elements is called a matrix
- Matrices are generally enclosed by brackets like
- Matrices are denoted by capital letters A, B, C and so on
- Elements in a matrix are real or complex numbers; real or complex real-valued functions.
Oder of Matrix: A matrix having rows and ‘n’ columns is said to be of order m x n. Read as m by n.
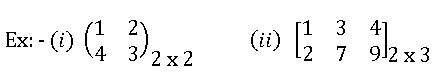
Types of Matrices
Square Matrix: A matrix in which the no. of rows is equal to the no. of columns is called a square matrix.

Principal diagonal ( diagonal) Matrix: If A = [aij] is a square matrix of order ‘n’ the elements a11 , a22 , a33 , ………. ann is said to constitute its principal diagonal.

Trace Matrix: The sum of the elements of the principal diagonal of a square matrix A is called the trace of the matrix. It is denoted by Tr (A).
Ex:-
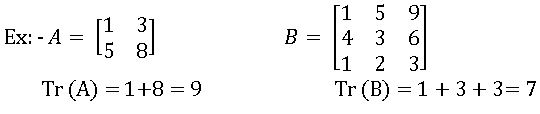
Diagonal Matrix: If each non-diagonal element of a square matrix is ‘zero’ then the matrix is called a diagonal matrix.

Scalar Matrix: If each non-diagonal elements of a square matrix are ‘zero’ and all diagonal elements are equal to each other, then it is called a scalar matrix.

Identity Matrix or Unit Matrix: If each of the non-diagonal elements of a square matrix is ‘zero’ and all diagonal elements are equal to ‘1’, then that matrix is called a unit matrix.
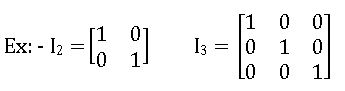
Null Matrix or Zero Matrix: If each element of a matrix is zero, then it is called a null matrix.

Row matrix & column Matrix: A matrix with only one row s called a row matrix and a matrix with only one column is called a column matrix.
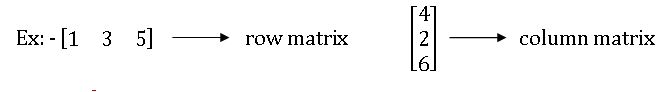
Triangular matrices:
A square matrix A = [aij] is said to be upper triangular if aij = 0 ∀ i > j
A square matrix A = [aij] is said to be lower triangular matrix aij = 0 ∀ i < j
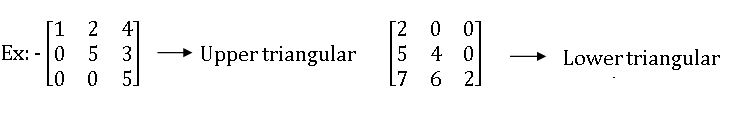
Equality of matrices: matrices A and B are said to be equal if A and B of the same order and the corresponding elements of A and B are equal.
![]()
Product of Matrices:
Let A = [aik]mxn and B = [bkj]nxp be two matrices ,then the matrix C = [cij]mxp where
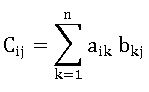
Note: Matrix multiplication of two matrices is possible when no. of columns of the first matrix is equal to no. of rows of the second matrix.
Transpose of Matrix: If A = [aij] is an m x n matrix, then the matrix obtained by interchanging the rows and columns is called the transpose of A. It is denoted by AI or AT.

Note: (i) (AI)I = A (ii) (k AI) = k . AI (iii) (A + B )T = AT + BT (iv) (AB)T = BTAT
Symmetric Matrix: A square matrix A is said to be symmetric if AT =A
If A is a symmetric matrix, then A + AT is symmetric.
Skew-Symmetric Matrix: A square matrix A is said to be skew-symmetric if AT = -A
If A is a skew-symmetric matrix, then A – AT is skew-symmetric
Minor of an element: Consider a square matrix
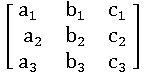
the minor an element in this matrix is defined as the determinant of the 2×2 matrix obtained after deleting the rows and the columns in which the element is present.

Cofactor of an element: The cofactor of an element in i th row and j th column of A3×3 matrix is defined as it’s minor multiplied by (- 1 ) i+j .
Properties of determinants:
- If each element of a row (column) of a square matrix is zero, then the determinant of that matrix is zero.

- If A is a square matrix of order 3 and k is scalar then.
- If two rows (columns) of a square matrix are identical (same), then Det. Of that matrix is zero.
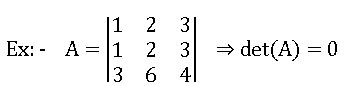
- If each element in a row (column) of a square matrix is the sum of two numbers then its determinant can be expressed as the sum of the determinants.
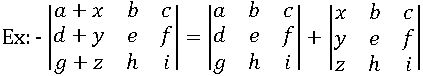
- If each element of a square matrix are polynomials in x and its determinant is zero when x = a, then (x-a) is a factor of that matrix.
- For any square matrix A Det(A) = Det (AI).
- Det(AB) = Det(A) . Det(B).
- For any positive integer n Det(An) = (DetA)n.
Singular and non-singular matrices: A Square matrix is said to be singular if its determinant is zero, otherwise it is said to be the non-singular matrix.

Ad joint of a matrix: The transpose of the matrix formed by replacing the elements of a square matrix A with the corresponding cofactors is called the adjoint of A.
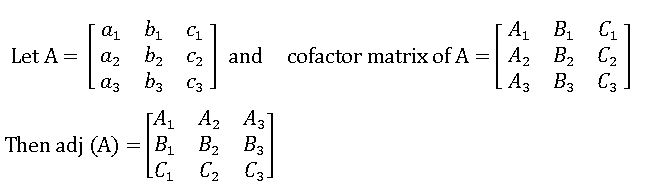
Invertible matrix: Let A be a square matrix, we say that A is invertible if there exists a matrix B such that AB =BA = I, where I is the unit matrix of the same order as A and B.
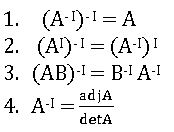
Augmented matrix: The coefficient matrix (A) augmented with the constant column matrix (D) is called the augmented matrix. It is denoted by [AD].
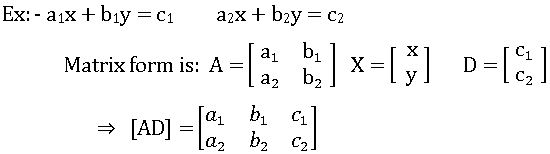
Sub matrix: A matrix obtained by deleting some rows and columns (or both) of a matrix is called the submatrix of the given matrix.
Let A be a non-zero matrix. The rank of A is defined as the maximum of the order of the non-singular submatrices of A.
- Note: If A is a non-zero matrix of order 3 then the rank of A is:
- 1, if every 2×2 submatrix is singular
- 2, if A is singular and at least one of its 2×2 sub-matrices is non-singular
(iii) 3, if A is non – singular.
Consistent and Inconsistent: The system of linear equations is consistent if it has a solution, in-consistent if it has no solution.
- Note: The system of three equations in three unknowns AX = D has
- A unique solution if rank(A) = rank ([AD]) = 3
- Infinitely many solutions if rank (A) = ([AD]) < 3
- No solution if rank (A) ≠ rank ([AD])
Solutions of a homogeneous system of linear equations:
The system of equations AX = 0 has
- The trivial solution only if rank(A) = 3
- An infinite no. of solutions if rank(A) < 3
4.ADDITION OF VECTORS
Directed line: If A and B are two distinct points in the space, the ordered pair (A, B) denoted by AB is called a directed line segment with initial point A and terminal point B.

⇒ A directed line passes through three characteristics: (i) length (ii) support (iii) direction
Scalar: A quantity having magnitude only is called a scalar. We identify real numbers as a scalar.
Ex: – mass, length, temperature, etc.
Vector: A quantity having length and direction is called a vector.
Ex: – velocity, acceleration, force, etc.
⇒ If ![]() is a vector then its length is denoted by
is a vector then its length is denoted by ![]()
Position of vector: If P (x, y, z) is any point in the space, then ![]() is called the position vector of the point P with respect to origin (O). This is denoted by
is called the position vector of the point P with respect to origin (O). This is denoted by ![]()
Like and unlike vectors: If two vectors are parallel and having the same direction then they are called like vectors.
If two vectors are parallel and having opposite direction then they are called, unlike vectors.
![]()
Coplanar vectors: Vectors whose supports are in the same plane or parallel to the same plane are called coplanar vectors.
VECTOR ADDITION
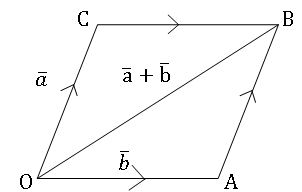
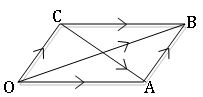
Triangle law: If ![]() are two vectors, there exist three points A, B, and C in a space such that
are two vectors, there exist three points A, B, and C in a space such that![]() defined by
defined by ![]()
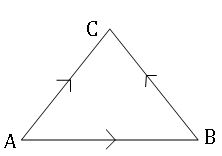
Parallelogram law: If two vectors![]() and
and ![]() represented by two adjacent sides of a parallelogram in magnitude and direction then their sum is represented in magnitude and direction by the diagonal of the parallelogram through their common point.
represented by two adjacent sides of a parallelogram in magnitude and direction then their sum is represented in magnitude and direction by the diagonal of the parallelogram through their common point.
Scalar multiplication: Let![]() be a vector and λ be a scalar then we define vector λ
be a vector and λ be a scalar then we define vector λ![]() to be the vector
to be the vector![]() if either
if either![]() is zero vector or λ is the scalar zero; otherwise λ
is zero vector or λ is the scalar zero; otherwise λ![]() is the vector in the direction of
is the vector in the direction of ![]() with the magnitude
with the magnitude ![]() if λ>0 and λ
if λ>0 and λ![]() = (−λ)(−
= (−λ)(−![]() ) if λ<0.
) if λ<0.

The angle between two non-zero vectors: Let![]() be two non-zero vectors, let
be two non-zero vectors, let ![]() then ∠AOB has two values. The value of ∠AOB, which does not exceed 1800 is called the angle between the vectors
then ∠AOB has two values. The value of ∠AOB, which does not exceed 1800 is called the angle between the vectors![]() and
and ![]() , it is denoted by (
, it is denoted by (![]() ).
).
Section formula: Let![]() be two position vectors of the points A and B with respect to the origin if a point P divides the line segment AB in the ratio m:n then
be two position vectors of the points A and B with respect to the origin if a point P divides the line segment AB in the ratio m:n then
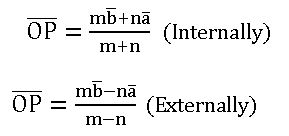
Linear combination of vectors: let ![]() be vectors x1, x2, x3…. xn be scalars, then the vector
be vectors x1, x2, x3…. xn be scalars, then the vector![]() is called the linear combination of vectors.
is called the linear combination of vectors.
Components: Consider the ordered triad (a, b, c) of non-coplanar vectors![]() If r is any vector then there exist a unique triad (x, y, z) of scalars such that
If r is any vector then there exist a unique triad (x, y, z) of scalars such that ![]() . These scalars x, y, z are called the components of
. These scalars x, y, z are called the components of ![]() with respect to the ordered triad (a, b, c).
with respect to the ordered triad (a, b, c).
- i, j, k are unit vectors along the X, Y and Z axes respectively and P(x, y, z) is any point in the space then
 = r = x i + y j +z k and
= r = x i + y j +z k and
Regular polygon: A polygon is said to be regular if all the sides, as well as all the interior angles, are equal.
- If a polygon has sides then the no. of diagonals of a polygon is

- The unit vector bisecting the angle between is

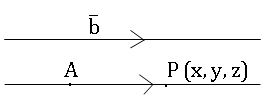
Vector equation of a line and plane
⇒The vector equation of the line passing through point A (![]() ) and ∥el to the vector
) and ∥el to the vector ![]() is
is
Proof:-
Then AP, are collinear vector proof: let P (![]() ) be any point on the line a
) be any point on the line a
the equation of the line passing through origin and parallel to the vector![]() is
is![]()
- the vector equation of the line passing through the points A(
 ) and B(
) and B(  ) is
) is 
- Cartesian equation of the line passing through A ( x1, y1, z1) and B ( x2, y2, z2) is

- The vector equation of the plane passing through point A(
 ) and parallel to the vectors
) and parallel to the vectors  and
and is
is 
- The vector equation of the plane passing through the point A(
 ), B(
), B( ) and parallel to the vector
) and parallel to the vector  is
is 
- The vector equation of the plane passing through the points A(
 ), B(
), B( ) and C(
) and C(  ) is
) is
5.PRODUCT OF VECTORS
Dot product (Scalar product): Let![]() are two vectors. The dot product or direct product of
are two vectors. The dot product or direct product of ![]() and
and ![]() is denoted by
is denoted by![]() and is defined as
and is defined as
⟹ If![]() > 0, then θ is an acute angle
> 0, then θ is an acute angle
⟹ If ![]() < 0, then θ is obtuse angle 0
< 0, then θ is obtuse angle 0
⟹ If ![]() = 0, then
= 0, then![]() is perpendicular to
is perpendicular to![]()
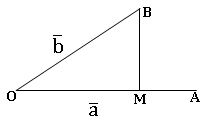
Component and Orthogonal Projection:
Let![]() =
=![]() ,
,![]() =
=![]() be two non-zero vectors. Let the plane passing through B (
be two non-zero vectors. Let the plane passing through B (![]() ) and perpendicular to
) and perpendicular to ![]() intersects
intersects![]()
In M, then ![]() is called the component of
is called the component of ![]() on
on ![]()
- The component (projection) vector of
 on
on  is
is 
- Length of the projection (component) =

- Component of
 perpendicular to
perpendicular to =
= 
If ![]() ,
,![]() ,
, ![]() form a right-handed system of an orthonormal triad, then
form a right-handed system of an orthonormal triad, then
In a parallelogram, the sum of the squares of the lengths of the diagonals is equal to the sum of the squares of the lengths of its sides.
In ∆ABC, the length of the median through vertex A is 
The vector equation of the plane whose perpendicular distance from the origin is p and unit normal drawn from the origin towards the plane is,![]()
•The vector equation of the plane passing through point A (![]() ) and perpendicular to the
) and perpendicular to the![]() is
is![]()
•If θ is the angle between the planes ![]() then
then 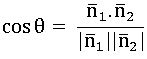
Cross product (vector product): Let ![]() and
and![]() be two non-zero collinear vectors. The cross product of
be two non-zero collinear vectors. The cross product of ![]() and
and ![]() is denoted by
is denoted by ![]() ×
×![]() (read as a cross ) and is defined as
(read as a cross ) and is defined as ![]()
•![]() are orthogonal triad then
are orthogonal triad then
• The vector![]() ×
×![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]() and also perpendicular to the plane containing them
and also perpendicular to the plane containing them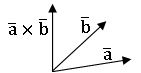
• The unit vector perpendicular to both![]() and
and ![]() is
is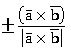
• If ![]() and
and ![]() are two sides of a triangle then the area of the triangle =
are two sides of a triangle then the area of the triangle =![]()
• If A (![]() ), B ()and C (
), B ()and C (![]() )are the vertices of a ∆ABC, then its area
)are the vertices of a ∆ABC, then its area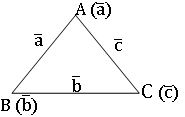
• The area of the parallelogram whose adjacent sides![]() and
and ![]() is
is ![]()
• The area of the parallelogram whose diagonals ![]() and
and ![]() is
is ![]()
• If A (![]() ), B (
), B (![]() )and C (
)and C (![]() )are three points then the perpendicular distance from A to the line passing through B, C is
)are three points then the perpendicular distance from A to the line passing through B, C is
Let![]() ,
,![]() and
and![]() be three vectors, then (
be three vectors, then (![]() ) .
) . ![]() is called the scalar triple product of
is called the scalar triple product of![]() ,
,![]() and
and![]() and it is denoted by
and it is denoted by![]()
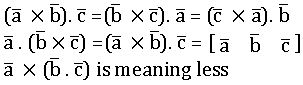
If![]()
![]() then
then
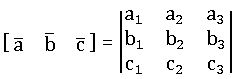
•In determinant rows(columns) are equal then the det. Value is zero.
•In a determinant, if we interchange any two rows or columns, then the sign of det. Is change.
•Four distinct points A, B, C, and D are said to be coplanar iff ![]()
The volume of parallelepiped:
If ![]() ,
,![]() and
and![]() are edges of a parallelepiped then its volume is
are edges of a parallelepiped then its volume is ![]()
The volume of parallelepiped:
The volume of Tetrahedron with![]() ,
,![]() and
and![]() are coterminous edges is
are coterminous edges is![]()
The volume of Tetrahedron whose vertices are A, B, C and D is ![]()
Vector equation of a plane:
The vector equation of the plane passing through point A (![]() ) and parallel to the vectors
) and parallel to the vectors![]() and
and ![]() is
is ![]()
The vector equation of the plane passing through the points A ( ![]() ) and B(
) and B( ![]() ) and parallel to the vector
) and parallel to the vector![]() is
is![]()
The vector equation of the plane passing through the points A (![]() ), B(
), B( ![]() ) and C(
) and C(![]() ) is
) is ![]()
Skew lines: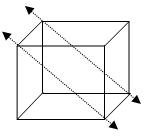
The lines which are neither intersecting nor parallel are called Skew lines
The shortest distance between the Skew lines:
If ![]() are two skew lines, then the shortest distance between them is
are two skew lines, then the shortest distance between them is 
If A, B, C and D are four points, then the shortest distance between the line joining the points AB and CD is 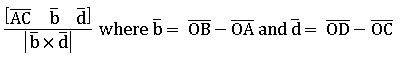
•The plane passing through the intersection of the planes![]() is
is ![]()
the perpendicular distance from point A (a ̅) to the plane ![]() is
is 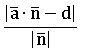
Let ![]() ,
,![]() and
and![]() be three vectors, then
be three vectors, then![]() is called the vector triple product of
is called the vector triple product of![]() ,
,![]() and
and![]() .
.
Scalar product of four vectors:
Vector product of four vectors:
6. TRIGONOMETRY UPTO TRANSFORMATIONS
The word ’trigonometry’ derived from the Greek words ‘trigonon’ and ‘metron’. The word ‘trigonon’ means a triangle and the word ‘metron’ means a measure.
Angle: An angle is a union of two rays having a common endpoint in a plane.
There are three systems of measurement of the angles.
- Sexagesimal system (British system)
- Centesimal system (French system)
- Circular measure (Radian system)
Sexagesimal system: – In this system, a circle can be divided into 360 equal parts. Each part is called one degree (0). One circle = 3600
Further, each degree can be divided into 60 equal parts. Each part is called one minute (‘).
and each minute can be divided into 60 equal parts. Each part is called one second (“)
Sexagesimal system: – In this system, a circle can be divided into 400 equal parts. Each part is called one grade (g). One circle = 400g
Further, each grade can be divided into 100 equal parts. Each part is called one minute (‘).
and each minute can be divided into 100 equal parts. Each part is called one second (“)
Circular measure: Radian is defined as the amount of the angle subtended by an arc of length ’r’ of a circle of radius ‘r’.
One radian is denoted by 1c. One circle = 2πc
Relation between the three measures:
3600 = 400g = 2 πc
1800 = 200g = πc
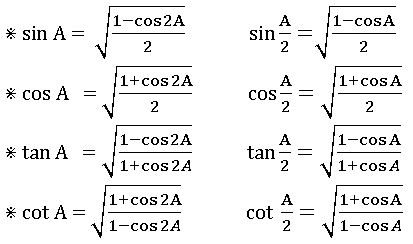
Trigonometric identities: –
∗ sin2θ + cos2θ = 1
1 – cos2θ = sin2θ
1 – sin2θ = cos2θ
∗ sec2θ − tan2θ = 1
sec2θ = 1 + tan2θ
tan2θ = sec2θ – 1
(secθ − tanθ) (secθ + tanθ) = 1
∗ cosec2θ − cot2θ = 1
co sec2θ = 1 + cot2θ
cot2θ = cosec2θ – 1
(cosec θ – cot θ) (cosec θ + cot θ) = 1
• sin θ. cosec θ = 1
sec θ. cos θ = 1
tan θ. cot θ = 1
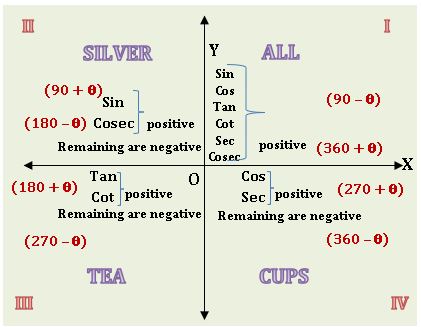
All Silver Tea Cups Rule:
Note: If 900 ±θ or 2700 ±θ then
‘sin’ changes to ‘cos’; ‘tan’ changes to ‘cot’; ‘sec’ changes to ‘cosec’
‘cos’ changes to ‘sin’; ‘cot’ changes to ‘tan’; ‘cosec’ changes to ‘sec’.
If 1800 ±θ or 3600 ±θ then, no change in ratios.
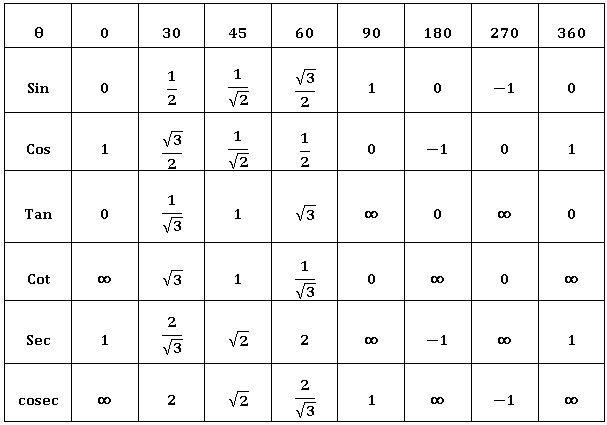
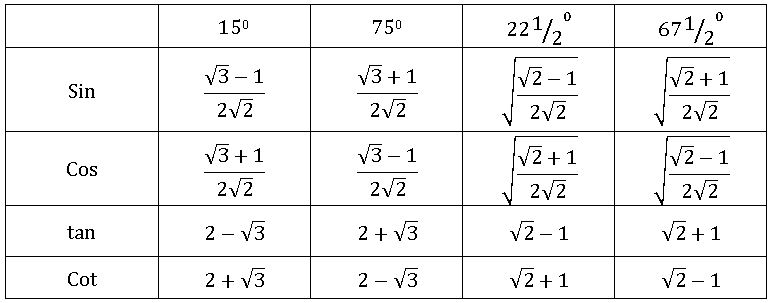
Values of Trigonometric Ratios:
Complementary angles: Two angles A and B are said to be complementary angles, if A + B = 900.
supplementary angles: Two angles A and B are said to be supplementary angles, if A + B = 1800.
Let E ⊆ R and f: E → R be a function, then f is called periodic function if there exists a positive real number ‘p’ such that
- (x + p) ∈ E ∀ x∈ E
- F (x+ p) = f(x) ∀ x∈ E
If such a positive real number ‘p’ exists, then it is called a period of f.
The algebraic sum of two or more angles is called a ‘compound angle’.
For any two real numbers A and B
⋇ sin (A + B) = sin A cos B + cos A Cos B
⋇ sin (A − B) = sin A cos B − cos A Cos B
⋇ cos (A + B) = cos A cos B − sin A sin B
⋇ cos (A − B) = cos A cos B + sin A sin B
⋇ sin (A + B + C) = ∑sin A cos B cos C − sin A sin B sin C
⋇ cos (A + B + C) = cos A cos B cos C− ∑cos A sin B sin C
⋇ sin (A + B) sin (A – B) = sin2 A – sin2 B = cos2 B – cos2 A
⋇ cos (A + B) cos (A – B) = cos2 A – sin2 B = cos2 B – sin2 A
Extreme values of trigonometric functions:
If a, b, c ∈ R such that a2 + b2 ≠ 0, then
If A is an angle, then its integral multiples 2A, 3A, 4A, … are called ‘multiple angles ‘of A and the multiple of A by fraction like![]() are called ‘submultiple angles.
are called ‘submultiple angles.
⋇ cos 2A = cos2 A – sin2 A
= 2 cos2 A – 1
= 1 – 2sin2 A
∎ If ![]() is not an add multiple of
is not an add multiple of ![]()
⋇ sin3A = 3 sin A −4 sin3 A
⋇ cos 3A = 4 cos3 A – 3 cos A
⋇ tan A + cot A = 2 cosec 2A
⋇ cot A – tan A = 2 cot 2A
For A, B∈ R
⋇ sin (A + B) + sin (A – B) = 2sin A cos B
⋇ sin (A + B) −sin (A – B) = 2cos A sin B
⋇ cos (A + B) + cos (A – B) = 2 cos A cos B
⋇ cos (A + B) − cos (A – B) = − 2sin A sin B
For any two real numbers C and D
If A + B + C = π or 1800, then
⋇ sin (A + B) = sin C; sin (B + C) = sin A; sin (A + C) = sin B
⋇ cos (A + B) = − cos C; cos (B + C) = −cos A; cos (A + C) = − cos B
⋇ sin ![]() = cos
= cos![]() ; sin
; sin![]() = cos
= cos![]() ; sin
; sin![]() = cos
= cos![]()
⋇ cos ![]() = sin
= sin![]() ; cos
; cos![]() = sin
= sin![]() ; cos
; cos ![]() = sin
= sin![]()
⋇ sin (A + B) = cos C; sin (B + C) = cos A; sin (A + C) = cos B
⋇ cos (A + B) = sin C; cos (B + C) = sin A; cos (A + C) = sin B
7. TRIGONOMETRIC EQUATIONS
Trigonometric equation: An equation consisting of the trigonometric functions of a variable angle θ ∈ R is called a ‘trigonometric equation’.
The solution of the equation: The values of the variable angle θ, satisfying the given trigonometric equation is called a ‘solution’ of the equation.
The set of all solutions of the trigonometric equation is called the solution set’ of the equation. A ‘general solution’ is an expression of the form θ0 + f(n) where θ0 is a particular solution and f(n) is a function of n ∈ Z involving π.
⨂ If k ∈ [− 1, 1] then the principle solution of θ of sin x = k lies in ![]()
General solution of sin x = sin θ is x = nπ + (−1) n θ, n ∈ Z
⨂ If k ∈ [− 1, 1] then the principle solution of θ of cos x = k lies in ![]()
General solution of cos x = cos θ is x = 2nπ ± θ, n ∈ Z
⨂ If k ∈R then the principle solution of θ of tan x = k lies in 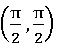
General solution of tan x = tan θ is x = nπ + θ n ∈ Z
⨂ If sin θ = 0, then the general solution is θ = nπ, n ∈ Z
⨂ If tan θ = 0, then the general solution is θ = nπ, n ∈ Z
⨂ If cos θ = 0, then the general solution is θ = (2n + 1)![]() , n ∈ Z
, n ∈ Z
⨂ If sin2 θ = sin2 𝛂, cos2 θ = cos2 𝛂 or tan2 θ = tann2 𝛂 then the general solution is 𝛉 = nπ ± θ, n ∈ Z
8.INVERSE TRIGONOMETRIC FUNCTIONS
If A, B are two sets and f: A→ B is a bijection, then f-1 is existing and f-1: B → A is an inverse function.
⨂ The function Sin-1: [−1, 1] →![]() is defined by Sin-1 x = θ ⇔ θ∈
is defined by Sin-1 x = θ ⇔ θ∈ ![]() and sin θ = x
and sin θ = x
⨂ The function Cos-1: [−1, 1] → [0, π] is defined by Sin-1 x = θ ⇔ θ∈ [0, π] and cos θ = x
⨂ The function Tan-1: R →![]() is defined by Tan-1 x = θ ⇔ θ∈
is defined by Tan-1 x = θ ⇔ θ∈![]() and tan θ = x
and tan θ = x
⨂ The function Sec-1: [−∞, −1] ∪ [1, ∞] →![]() is defined by Sin-1 x = θ ⇔ θ∈
is defined by Sin-1 x = θ ⇔ θ∈![]() and sec θ= x
and sec θ= x
⨂ The function Cosec-1: [−∞, −1] ∪ [1, ∞] →![]() is defined by cosec-1 x = θ ⇔ θ∈
is defined by cosec-1 x = θ ⇔ θ∈![]() and Cosec θ= x
and Cosec θ= x
⨂ The function Cot-1: R → (0, π) is defined by Cot-1 x = θ ⇔ θ ∈ (0, π) and cot θ = x
Properties of Inverse Trigonometric functions:
⨂ Sin-1 x = Cosec-1(1/x) ∀ x ∈ [−1, 1] – {0}
⨂ Cos-1x = Sec-1(1/x) ∀ x ∈ [−1, 1] – {0}
⨂ Tan-1 x = Cot-1(1/x), if x > 0
⨂ Tan-1 x = Cot-1(1/x) −π, if x < 0
⨂ Sin-1 (−x) = − Sin-1(x) ∀ x ∈ [−1, 1]
⨂ Cos-1 (−x) = π − Cos-1(x) ∀ x ∈ [−1, 1]
⨂ Tan-1 (−x) = − Tan-1(x) ∀ x ∈ R
⨂ Cosec-1 (−x) = − Cose-1(x) ∀ x ∈ (− ∞, − 1] ∪ [1, ∞)
⨂ Sec-1 (−x) = π − Sec-1(x) ∀ x ∈ (− ∞, − 1] ∪ [1, ∞)
⨂ Cot-1 (−x) =π − Cot-1(x) ∀ x ∈ R
⨂
(i) If θ∈![]() , then Sin−1(sin θ) = θ and if x ∈ [−1, 1], then sin (Sin−1x) = x
, then Sin−1(sin θ) = θ and if x ∈ [−1, 1], then sin (Sin−1x) = x
(ii) If θ∈ [0, π], then Cos−1(cos θ) = θ and if x ∈ [−1, 1], then cos (Cos−1x) = x
(iii) If θ∈![]() , then tan−1(tann θ) = θ and if x ∈ R, then tan (Tan−1x) = x
, then tan−1(tann θ) = θ and if x ∈ R, then tan (Tan−1x) = x
(iv) If θ∈ (0, π), then Cot−1(cot θ) = θ and if x ∈ R, then cot (Cot−1x) = x
(v) If θ∈ [0, ![]() ) ∪ (
) ∪ (![]() , π], then Sec−1(sec θ) = θ and
, π], then Sec−1(sec θ) = θ and
if x ∈ (− ∞, − 1] ∪ [1, ∞), then sec (Sec−1x) = x
(vi) If θ∈ ![]() , then Cosec−1(cosec θ) = θ and
, then Cosec−1(cosec θ) = θ and
if x ∈ (− ∞, − 1] ∪ [1, ∞), then cosec (Cosec−1x) = x
⨂
(i) If θ∈![]() , then Cos−1(sin θ) =
, then Cos−1(sin θ) = ![]()
(ii) If θ∈ [0, π], then Sin−1(cos θ) =![]()
(iii) If θ∈![]() , then Cot−1(tan θ) =
, then Cot−1(tan θ) =![]()
(iv) If θ∈ (0, π), then Tan−1(cot θ) =![]()
(v) If θ∈ ![]() , then Cosec−1(sec θ) =
, then Cosec−1(sec θ) =![]()
(vi) If θ∈![]() , then Sec−1(cosec θ) =
, then Sec−1(cosec θ) =![]()
⨂
- Sin−1x = Cos−1 (
 )if 0 ≤ x ≤ 1 and Sin−1x =− Cos−1 (
)if 0 ≤ x ≤ 1 and Sin−1x =− Cos−1 (  ) if −1 ≤ x ≤ 0
) if −1 ≤ x ≤ 0 - Sin−1x = Tan−1
 if x ∈ (−1, 1)
if x ∈ (−1, 1) - Cos−1x = Sin−1 (
 ) if x ∈ [0, 1] and Cos−1x = π − Sin−1 (
) if x ∈ [0, 1] and Cos−1x = π − Sin−1 ( ) if x ∈ [−1, 0]
) if x ∈ [−1, 0]
⨂ Cos−1 x + Sin−1x = ![]() ∀ x ∈ [−1, 1]
∀ x ∈ [−1, 1]
⨂ Sec−1 x + Cosec−1x = ![]() ∀ x ∈ (−∞, −1] ∪ [1, ∞)
∀ x ∈ (−∞, −1] ∪ [1, ∞)
⨂ Sin−1 x + Sin−1y = Sin−1(x ![]() + y
+ y![]() ) if 0 ≤x ≤ 1, 0 ≤y ≤ 1and x2 + y2 ≤ 1
) if 0 ≤x ≤ 1, 0 ≤y ≤ 1and x2 + y2 ≤ 1
=π− Sin−1(x ![]() + y
+ y ![]() ) if 0 ≤x ≤ 1, 0 ≤y ≤ 1and x2 + y2 > 1
) if 0 ≤x ≤ 1, 0 ≤y ≤ 1and x2 + y2 > 1
⨂ Cos−1 x + Cos−1y = Cos−1(x y −![]()
![]() ) if 0 ≤x, y ≤ 1and x2 + y2 ≥ 1
) if 0 ≤x, y ≤ 1and x2 + y2 ≥ 1
=π− Cos−1(x y −![]()
![]() ) if 0 ≤x ≤ 1, 0 ≤y ≤ 1and x2 + y2 < 1
) if 0 ≤x ≤ 1, 0 ≤y ≤ 1and x2 + y2 < 1
⨂ Tan−1 x + Tan−1y = Tan−1![]() if x > 0, y> 0 and xy < 1
if x > 0, y> 0 and xy < 1
=π + Tan−1 ![]() if x > 0, y> 0 and xy > 1
if x > 0, y> 0 and xy > 1
= Tan−1 ![]() if x < 0, y< 0 and xy > 1
if x < 0, y< 0 and xy > 1
= −π + Tan−1![]() if x < 0, y< 0 and xy < 1
if x < 0, y< 0 and xy < 1
⨂ Tan−1 x − Tan−1y = Tan−1 ![]() if x > 0, y> 0 or x < 0, y< 0
if x > 0, y> 0 or x < 0, y< 0
⨂ 2 Sin−1 x = Sin−1 (2x ) if x≤![]()
⨂ 2 Cos−1 x = Cos−1(2x2 – 1) if x ≥![]()
⨂ 3Sin−1x = Sin−1(3x – 4x3)
⨂ 3Cos−1x = Cos−1(4x3 – 3x)
9.HYPERBOLIC FUNCTIONS
⨂ The function f: R→R defined by f(x) = ∀ x ∈ R is called the ‘hyperbolic sin’ function. It is denoted by sinh x.
Similarly,
Identities:
⨂ cosh2x – sinh2 x = 1
cosh2x = 1 + sinh2 x
sinh2 x = cosh2 x – 1
⨂ sech2 x = 1 – tanh2 x
tanh2 x = 1 – sech2 x
⨂ cosech2 x = coth2 x – 1
coth2 x = 1 + coth2 x
Addition formulas of hyperbolic functions:
⨂ sinh (x + y) = sinh x cosh y + cosh x sinh y
⨂ sinh (x − y) = sinh x cosh y − cosh x sinh y
⨂ cosh (x + y) = cosh x cosh y + sinh x sinh y
⨂ cosh (x − y) = cosh x cosh y − sinh x sinh y
⨂ sinh 2x = 2 sinh x cosh 2x = ![]()
⨂ cosh 2x = cosh2x + sinh2 x = 2 cosh2x – 1 = 1 + 2 sinh2x =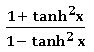
⨂ sinh 3x = 3 sinh x + 4 sinh3x
⨂ cosh 3x = 4 cosh3 x – 3 cosh x
Inverse hyperbolic functions:
⨂ Cosech−1x = 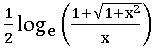 if x < 0 and x ∈ (−∞, 0)
if x < 0 and x ∈ (−∞, 0)
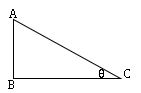
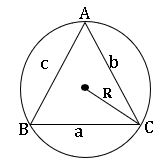
10. PROPERTIES OF TRIANGLES
Lengths AB = c; BC = a; AC =b
Area of the tringle is denoted by ∆.
Perimeter of the triangle = 2s = a + b + c
A = ∠CAB; B = ∠ABC; C = ∠BCA.
R is circumradius.
Sine rule:
In ∆ABC,
⟹ a = 2R sin A; b = 2R sinB; c = 2R sin C
Where R is the circumradius and a, b, c, are lengths of the sides of ∆ABC.
Cosine rule:
In ∆ABC,
a2 = b2 + c2 – 2bc cos A ⟹cos A = ![]()
b2 = a2 + c2 – 2ac cos B ⟹ cos B = 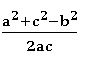
c2 = a2 + b2 – 2ab cos C ⟹ cos A = 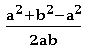
projection rule:
In ∆ABC,
a = b cos C + c cos B
b = a cos C + c cos A
c = a cos B + b cos A
Tangent rule (Napier’s analogy):
In ∆ABC,
Half angle formulae and Area of the triangle: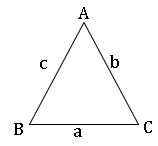
In ∆ABC, a, b, and c are sides
Maths ia Concept
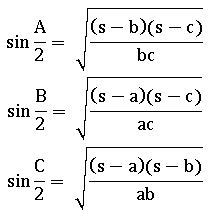
1.Half angle formulae: –
2.Formulae for ∆: –
∆ = ½ ab sinC= ½ bc sin A=½ ac sin B
= 2R2sin A sin B sinC
= r.s
In circle and Excircles of a triangle:
⋇The circle that touches the three sides of an ∆ABC internally is called ‘incircle’. The centre of the incircle is ‘I’ and the radius is ‘r’.
Formulae for ‘r’: –
= (s – a) tan![]() = (s – b) tan
= (s – b) tan![]() = (s – c) tan
= (s – c) tan![]()
⋇ The circle that touches the side BC internally and the other two sides AB and AC externally is called the ‘Excircle’ opposite to the angle A. Its centre is I1 and the radius is r1. A 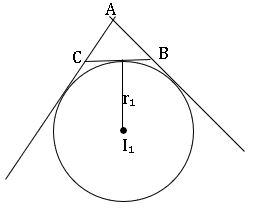 triangle has three ex circles. The remaining circles centre and radius are respectively I2, r2 and I3, r3.
triangle has three ex circles. The remaining circles centre and radius are respectively I2, r2 and I3, r3.
Formulae for ‘r1’: –
Formulae for ‘r2’: –
Formulae for ‘r3’: –
Maths ia Concept
Visit My Youtube Channel: Click on the Logo