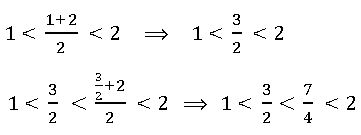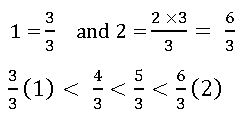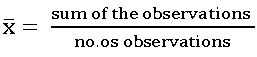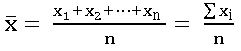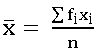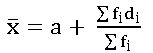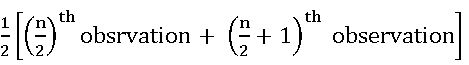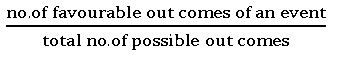ix Class Maths Concept
ix Class Maths
- TS 6th Maths Concept
- TS 7th Maths Concept
- TS 8th Maths Concept
- TS 9th Maths Concept
- TS 10th Maths Concept
TS IX CLASS MATHS CONCEPT
Studying maths in IX class successfully means that children take responsibility for their own learning and learn to apply the concepts to solve problems.
This note is designed by the ‘Basics in Maths’ team. These notes to do help students fall in love with mathematics and overcome fear.
1.REAL NUMBERS
Rational numbers:-
- The numbers which are written in the form of
 , where p, q are integers and q≠ 0 are called rational numbers. Rational numbers are denoted by Q.
, where p, q are integers and q≠ 0 are called rational numbers. Rational numbers are denoted by Q.
ex:- 3/2, 3/5, 2, 1 and so on
- Natural numbers, Whole numbers, and Integers are rational numbers.
- The rational numbers do not have a unique representation.
Representation of rational number:

To find a rational number between given numbers:
Mean method:- A rational number between two numbers a and b is 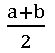
Ex:- insert two rational number between 1 and 2
To find a rational number in a single step:-
Ex:- insert two rational number between 1 and 2
To find two rational numbers, we 1 and 2 as rational numbers with same denominator 3 (∵ 1 + 2 = 3)
The decimal form of rational numbers:
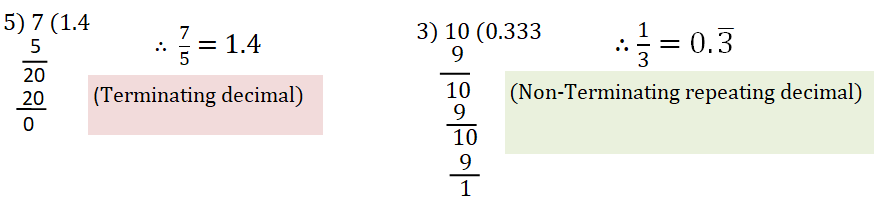
- Note:- Every rational number can be expressed as a terminating decimal or non-terminating repeating decimal.
- Converting decimal form into a fraction:
- Terminating decimals:- (i) 1.2 = 12/10 = 6/5
(ii) 1.35 =135/100 = 135/100 = 27/20
- Non-Terminating repeating decimals:-
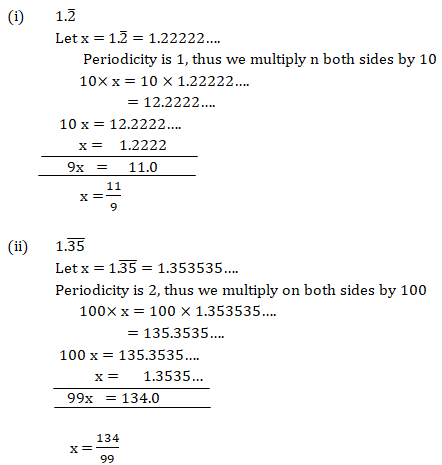
Irrational numbers:
- The numbers which are not written in the form of, where p, q are integers and q ≠ 0 are called rational numbers. Rational numbers are denoted by QI or S.
- Every irrational number can be expressed as a non-terminating decimal or non-repeating decimal.
Calculation of square roots:
- There is a reference of irrationals in the calculation of square roots in Sulbha Sutra.
- Procedure to find
 value:
value:

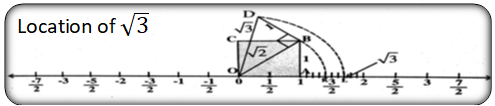
Representing irrational numbers on a number line:
- At ‘O’ draw a unit square OABC on a number line with each side 1 unit in length.
- By Pythagoras theorem OB2 = OA2 + AB2
= 12 + 12
OB2 = 2
- Using a compass with centre O and radius OB, draw an arc on the right side to O intersecting the number line at the point
- The location of
 is now at k.
is now at k.
- Note:- If a and b are two positive rational numbers such that ab is not a perfect square, this an irrational number lies between a and b.
Real numbers
- The collection of all rational and irrational numbers is called real numbers.
- Real numbers cover all the points on the number line.
- Every real number is represented by a unique point on the number line.
- Ex:-
 are some examples of real numbers.
are some examples of real numbers.
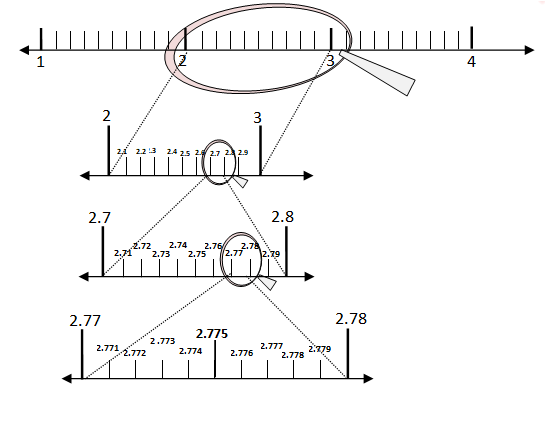
Representing real numbers on the number line through successive magnifications:-
locating 2. 775 on a number line
Operation on real numbers
- The sum, difference, product and quotient of irrational numbers need not be an irrational number.
- Irrational numbers are not closed under addition, subtraction, multiplication, and division.
- For any two real numbers a and b
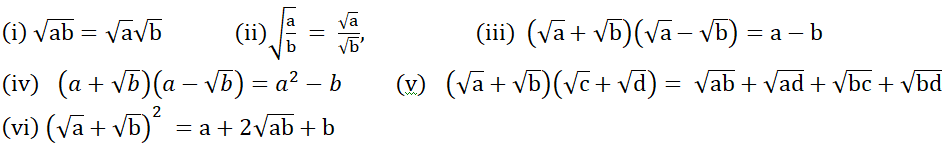
Rationalizing the denominator:
- Rationalizing factor(R.F):-If the product of two irrational numbers is rational, then each of the two is the rationalizing factor to others.
- The rationalizing factor of a given irrational number is not unique. It is convenient to use the simplest of all R.F.s of given irrational number.
- Note:-
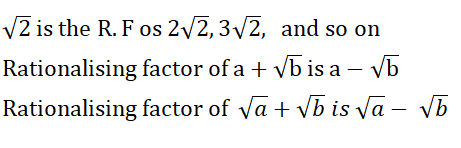
Law of exponents for real numbers:
2. POLYNOMIALS AND FACTORIZATION
Polynomial: An algebraic expression in which the variables involved have only whole number powers is called a polynomial.
Ex: x2 , x3 + 1, x2 + xy + y2 and so on.
Polynomials in one variable: The polynomials which are in the form of (a constant) × (some power of variable) are called polynomials in one variable.
Ex: 2x, 4x, 3x2 + 1 and so on.
Degree of the polynomial: The degree of a term is the sum of the exponent of its variable factors. The degree of the polynomial is the highest power of its variable term.
Ex: degree of 3x2 + 2x3 + 1 is 3
degree of 5x2y3 + 2xy + 3x3 is 5
a polynomial in one variable x of degree n is anxn + an-1xn-1 + …+a1x + a0. Where a0, a1…an are constants and an ≠ 0.
Types of polynomials:
- According to no. of terms: –
| No. of non-zero terms | Name of the polynomial | Examples | Terms |
| 1 | Monomial | 3x | 3x |
| 2 | Binomial | -2 x + 7 | -2x, 7 |
| 3 | Trinomial | 5x2 + 4x + 2 | 5x2, 4x, 2 |
| More than 3 | Multinomial | 6x3 – 5x2 + 7x – 3 | 6x3, -5x2, x, -3 |
According to a degree: –
| Degree of the polynomial | Name of the polynomial | Example |
| Not defined | Zero polynomial | 0 |
| 0 | Constant polynomial | -12, 4, 7 etc. |
| 1 | Linear polynomial | 2x+3, x – 3 etc. |
| 2 | Quadratic polynomial | 2x2 + 3x + 1, x2 – 4 etc. |
| 3 | Cubic polynomial | 3x3 – 4x2 + 2x + 6 |
| 4 | Bi quadratic polynomial | 4x4 + 2x3 + 45x2 +9x + 7 |
Zero of the polynomial: Let p(x) be a polynomial, if p(x) = 0 then, x is the zero of the polynomial p(x).
Ex: p(x) = 2x – 2
P(1) = 2(1) – 2 = 2 – 2 = 0
∴ 1 is the zero of the polynomial.
Zero of the linear polynomial in one variable:
| Linear polynomial | Zero of the polynomial |
| x+ a | – a |
| x – a | a |
| ax + b | -b/a |
| ax – b | b/a |
Dividing polynomials:
If p(x) is divided by g(x), then there exists quotient polynomial q(x) and remainder r(x) such that
p(x) = q(x) × g(x) + r(x)
this is called division algorithm for polynomials.
Remainder theorem:
Let p(x) be a polynomial of degree greater than or equal to one and let a be any real number. If p(x) is divided by the linear polynomial (x – a), then the remainder is p(a).
Ex: if p(x) = 3x2 – 4 x + 2 is divided by the polynomial (x – 1), then find remainder.
Ans: Given p(x) = 3x2 – 4 x + 2
Remainder is p (1)
⇒ p (1) = 3(1)2 – 4 (1) + 2 = 3 – 4 + 2 = 5 – 4 = 1
∴ remainder is 1.
Factor theorem:
If p(x) s a polynomial of degree greater than or equal to one and a is any real number, then x – a is a factor of p(x), if p(a) = 0 and its converse if (x – a) is a factor of p(x), then p(a) = 0.
Ex: if p(x) = x2 – 2x + 1, then show that (x – 1) is a factor of p(x)
Ans: given polynomial is p(x) = x2 – 2x + 1
P (1) = (1)2 – 2(1) + 1 = 1 – 2 + 1 = 2 – 2 = 0
∴ x – 1is the factor of x2 – 2x + 1.
Algebraic identities:
(i ) (x + y)2 ≡ x2 + 2xy + y2 (ii) (x − y)2≡x2 − 2xy + y2 (iii) (x + y)(x – y)≡x2 – y2
(iv) (x + a) (x + b) ≡ x2 + (a + b) x + ab (v) (x + y + z)2 ≡ x2 + y2 + z2 + 2xy + 2yz + 2zx
(v) (x +y)3 ≡ x3 + 3x2y + 3xy2 + y3 ≡ x3 + y3 + 3xy (x + y)
(vi) (x − y)3 ≡ x3 − 3x2y + 3xy2 + y3 ≡ x3 − y3 + 3xy (x − y)
(vii) (x + y + z)(x2+ y2 + z2 – xy – yz – zx) ≡ x3 + y3 + z3 – 3xyz.
3.THE ELEMENTS OF GEOMETRY
Geometry: The word geometry derived from the Greek word ‘geo’ means earth and ‘metron’ means measure.
Euclid’s Elements: Euclid wrote 13 books called ‘The Elements’. Euclid creates the first system of thought based on fundamental definitions, axioms, propositions rules of inference or logic.
Some definitions of Euclid’s 1st book of Elements are: (i) A ‘point’ is that that which has no part. (ii) A ‘line’ is the breathless length. (iii) The ends of a line are points. (iv) A straight line is a line which lies evenly with the points itself. (v) A ‘surface’ is that which has length and breadth only. (vi) The edge of the surface are lines. (vii) A plane surface is a surface which lies evenly with the straight lines on itself.
Note: In geometry, a point, a line and a plane are undefined terms.
Axioms: Axioms are statements that are self-evident or assumed to be true within the context of a particular mathematical system. Axioms are elf evident facts and do not require any proof.
Some of Euclid’s Axioms are:
- Things which are equal to the same things are equal to another.
- If equals are added to equals, the wholes are equal.
- If equals are subtracted from equals, the remainders are also equal.
- Things which coincide with one another are equal.
- Things which are double of the same things are equal.
- Things that are halves of the same things are equal.
Postulates: Postulates are used for the assumptions made in the geometry.
Euclid’s five postulates:
Postulate – 1: There is a unique line that passes through the given two distinct points.
Postulate – 2: A-line segment can be extended on either side to form a straight line.
Postulate –3: We can escribe a circle with any centre and any radius.
Postulate – 4: All right angles are equal.
Postulate – 5: If a straight line falling on two straight line makes the interior angles on the same side of it taken together is less than two right angles, then two straight lines, if produced infinitely, meet on that side on which the sum of the angles is less than two right angles.

Equivalent versions of Euclid’s fifth postulate:
From the fig. sum of the angles, x and y is less than 1800
- Through a point not on a given line, exactly one parallel line may be drawn o the given line (John Playfair).
- The sum of the angles of any triangle is constant and is equal to two right angles (Legendre).
- If a straight line intersects any one of two parallel lines, then it will intersect others also (Proclus).
- Straight lines parallel to the same straight line are parallel to one another (Proclus).
Conjecture or Hypothesis: The statements which are neither proved nor disproved are called conjectures.
4. LINES AND ANGLES
Line: Line can be extended in both directions endlessly.
Ray: It is a part of the line. It begins at a point and goes on endlessly in a specific direction.
Line segment: A part of the line with two endpoints is called a line segment.
Collinear points: If three or more points lie on the same line, then they are called collinear points.
A B and C are collinear points
Note: if ‘n’ points lie on a line, then no. of line segments = ![]()
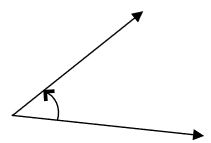
Angle: An angle is formed when two rays originate from the same point. The rays making an angle are called ‘Arms’ of the angle. The common point is called ‘vertex’.
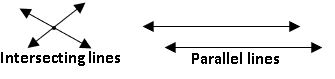
Intersecting and Non-intersecting lines: If two lines meet at any point, then the lines are intersecting lines. If two lines never meet at any point are called non-intersecting lines or parallel lines.
Concurrent lines: If two or more lines meet at the point, then that lines are called concurrent lines.
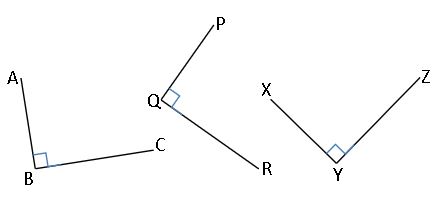
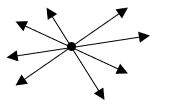 Complementary angles: Two angles are said to be complementary angles if their um is 900.
Complementary angles: Two angles are said to be complementary angles if their um is 900.
The complementary angle of x0 is 900 – x0.
Supplementary angles: Two angles are said to be supplementary angles if their um is 1800.
the supplementary angle of x0 is 1800 – x0.
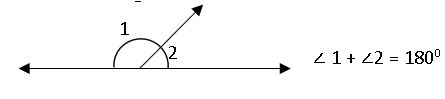
Linear pair of angles: If a ray stands on a straight line, then the sum of the two adjacent angles is so formed is 1800.
Note: If the sum of two adjacent angles is 1800, then they are called linear pairs of angles.
If the sum of two adjacent angles is 1800, then they are called linear pairs of angles.
Note: – if the sum of two adjacent angles is 1800, then non-common arms of the angles form a line. This is the converse of a linear pair of angle axiom.
Angles at a point: We know that the sum of all the angles around a point is always 3600.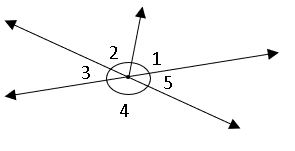
From the figure ∠ 1 + ∠2 ∠ 3 + ∠4 ∠5 = 3600
Vertically opposite angles: When two lines intersect at a point, the angles with the same vertex and have no common arm are called vertically opposite angles.

Note: If two lines intersect each other, then the pairs of vertically opposite angles are equal.
∠AOD, ∠BOC; ∠AOC, ∠BOD are vertically opposite angles.
⟹ ∠AOD = ∠BOC; ∠AOC = ∠BOD.
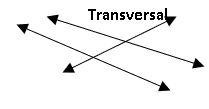
Lines and a transversal:
Transversal: A-line that intersects two or more lines at distinct points is called a transversal.
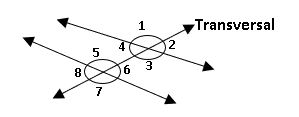
∠1, ∠2, ∠7 and ∠8 are exterior angles
∠3, ∠4, ∠5 and ∠6 are interior angles
Corresponding angles: –
Two angles which are lies the same side of the transversal and one interior and another one exterior are called corresponding angles.
∠1, ∠5; ∠2, ∠6; ∠3, ∠7 and ∠4, ∠8
Alternate angles: –
Two angles which are the lies opposite sides of the transversal and both interior or exterior are called corresponding angles.
∠1, ∠7; ∠2, ∠8 are exterior alternate angles
∠3, ∠5; ∠4, ∠6 are interior alternate angles.
∠3, ∠6; ∠4, ∠5 interior angles the same side of the transversal.
Transversal on parallel lines:
∗ If pair of parallel lines are intersected by a transversal then the angles each pair of corresponding angles are equal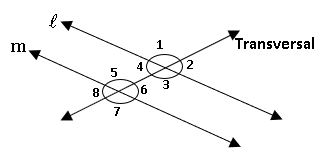
⇒ ∠1, =∠5; ∠2= ∠6; ∠3= ∠7 and ∠4= ∠8
∗ If pair of parallel lines are intersected by a transversal then the angles each pair of interior alternate angles are equal.
∠3= ∠5; ∠4= ∠6
∗ If pair of parallel lines are intersected by a transversal then the angles each pair of exterior alternate angles are equal.
∠1= ∠7; ∠2= ∠8
∗ If pair of parallel lines are intersected by a transversal then the angles each pair of interior angles in the same side of the transversal are supplementary.
∠3+∠6= 1800; ∠4+ ∠5 = 1800
Note:
- If a transversal intersects two lines and the pair of corresponding angles are equal, then the lines are parallel.
- If a transversal intersects two lines and the pair of alternate angles are equal, then the lines are parallel.
- If a transversal intersects two lines and the interior angles on the same side of the transversal are supplementary, then the lines are parallel.
Note: Lines that are parallel to the same line are parallel to each other.
Angle-sum property of a triangle:
The sum of the angles in a triangle is 1800
∠A + ∠B + ∠C = 1800
An exterior angle of a triangle:
When one side of the triangle is produced, the angle thus formed is called the exterior angle. Exterior angle property:- The exterior angle of a triangle is equal to the sum of two interior opposite angles. 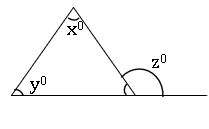
x0+ y0 = z0
5.CO-ORDINATE GEOMETRY
The representation of a point on a plane with the idea of two references led to the development of a new branch of mathematics is known as Co-ordinate geometry.
Rene Descartes (1595 – 1650) developed the study of coordinate geometry. He found an association between algebraic equations and geometric curves and figures.
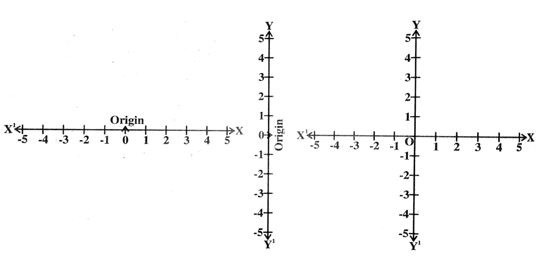
Cartesian system:
We use number line by making points on the line at equal distance.
Take two number line, perpendicular to each other in the plane. We locate the position of points concerning these lines
The point of intersection of these number lines is Origin it is denoted by ‘O’. The horizontal number line is XXI is called X-axis and the vertical number line YYI s called as Y-axis.
OX is a positive X-axis, OXΙ is a negative X-axis.
OY is a positive Y-axis, OYI is a negative Y-axis.
- The distance of a point from Y-axis is called x co-ordinate or
- The distance of a point from X-axis is called y co-ordinate or
- The co-ordinates of origin are (0,0).
- The x coordinate of a point on y-axis is 0.
- They c-ordinate of a point on y-axis is 0.
- Equation of x- axis is y = 0.
- Equation of y- axis is x = 0.
6.LINEAR EQUATIONS IN TWO VARIABLES
Equation: The expression which is connected by equality symbol (=) is called an equation.
Ex: x = 5, x + y = 2, x2 = 2y etc.
Linear equation: If the degree of the equation is 1, then it is called a linear equation.
Ex: x + 2y = 4, 3x – 5 = 0, 4y = 6 etc.
Linear equation in one variable: If a linear equation has only one variable, then it is called ‘linear equation in one variable’.
Ex: x + 3 = 4, 4x – 4 = 0, y – 3 = 0 etc.
Linear equation in two variables: If a linear equation has two variables, then it is called ‘linear equation in two variables.
Ex: x + 3y = 4, 4x – 4y = 0, y – 3x = 0 etc.
General form:
The general form of linear equation in two variables ‘x’ and ‘y’ is ax + by c = 0, where a, b, c are real numbers and a ≠ 0, b ≠ 0.
Solution: Any pair of values of ‘x’ and ‘y’ which satisfies the linear equations in two variables is called its solution.
Ex: x + y = 3
x = 2, y =1; x =1, y =2, x =0, y =3; x =3, y = 0 are some solutions of above equation.
∴ For a linear equation in two variables, we can find many solutions.
Note: An easy way of getting two solutions is put x = 0 and get the corresponding value of y. Similarly, we can put y= 0 and get the corresponding value of x.
Graph of linear equation in two variables:
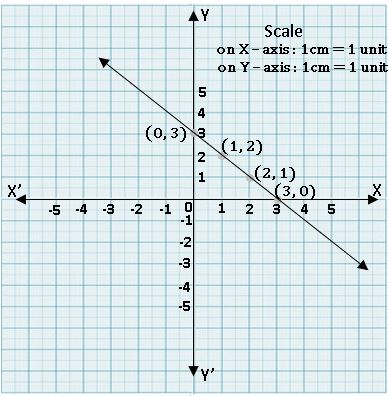
Ex: x + y = 3
Sol: Given equation is x + y = 3
y = 3 – x
| x | 0 | 1 | 2 | 3 |
| y = 3 – x | 3 | 2 | 1 | 0 |
| (x, y) | (0, 3) | (1, 2) | (2, 1) | (3, 0) |
Steps to draw the graph of the linear equations in two variables:
- Write the linear equation.
- Put x = 0 in the given equation and find the corresponding value of y.
- Put y = 0 in the given equation and find the corresponding value of x.
- Write the values of ‘x’ and its corresponding value of ‘y’ as coordinates of x and y respectively as (x, y) form.
- Plot the points on graph paper.
- Join these points.
Observations from the graph:
- Every solution of the linear equation in two variables represents a point on the line of the equation.
- Every point on this line is a solution to the linear equation in two variables.
- Any point that does not lie on this line not a solution to the equation.
- The collection points that give the solution of the linear equation in two variables is the graph of the linear equation.
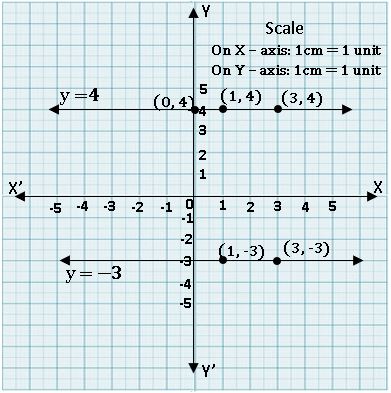
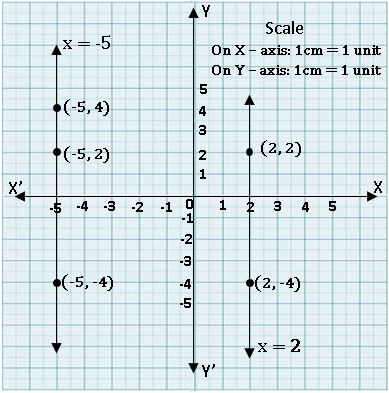
Equation of the line parallel to X-axis:
Equation of X – axis is y = 0.
Equation of any line parallel to X-axis is y = k, where k is the distance from above or below of the X-axis.
Equation of the line parallel to Y-axis:
Equation of Y – axis is x = 0.
Equation of any line parallel to Y-axis is x = k, where k is the distance from left or right of the Y-axis.
7.TRIANGLES
Triangle: A figure made up of three-line segments is called a triangle.
Congruent figures: The figures which have the same shape and same size are called congruent figures.
If two-line segments have equal in length, then they are congruent.
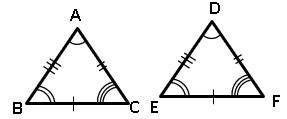
Congruency of Triangles:
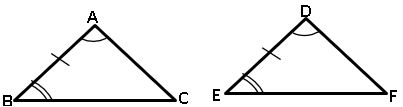
Two triangles are said to be congruent if (i) their corresponding angles are equal (ii) their corresponding sides are equal.
Ex: In ∆ ABC, ∆ DEF
∠A ≅ ∠D; ∠B≅ ∠E; ∠C ≅ ∠F
AB ≅ DE; BC≅ EF; AC ≅ DF
∴∆ABC ≅ ∆DEF
If two triangles are congruent, then corresponding parts of congruent triangles are equal (CPCT)
The criterion for congruency of Triangles:
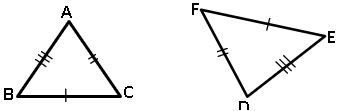
1.Side -Side -Side congruency (SSS):
If three side of a triangle is equal to the corresponding three sides of another triangle, then the triangles are congruent.
∴ ∆ABC ≅ ∆DEF
2. Side -Angle -Side congruency (SAS):
If two sides and the angle included between the two sides of a triangle are equal to the corresponding two sides and the included angle of another triangle, then the triangles are congruent.
∴ ∆ABC ≅ ∆DE
3.Angle – Side -Angle congruency (ASA):
If two angles and included side of a triangle are equal to the corresponding two angles and included side of another triangle, then the triangles are congruent.
∴ ∆ABC ≅ ∆DEF
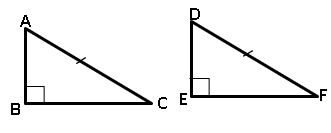
4.Right angle – Hypotenuse – Side congruence (RHS):
If the hypotenuse and one side of a right-angled triangle are equal to the corresponding hypotenuse and side of the other right-angled triangle, then the triangles are Equal.
∴∆ABC ≅ ∆DEF
5.A.S congruence: If two triangles are congruent if any two pairs of angles and one pair of corresponding angles are equal.
Some properties of the triangle:
1.Angles opposite to the equal side of an Isosceles triangle is equal.
2.The sides opposite to equal angles of a triangle are equal.
In equalities in a triangle:
1.If two sides of a triangle are equal, the angles opposite to the longer side is larger.
2.In any triangle, the side opposite to larger angle is longer.
3.The sum of any two sides of the triangle is greater than the third side.
4.The difference of any two sides of a triangle is less than the third side.
8.QUADRILATERALS
Quadrilateral: A closed figure made up of four-line segments is called Quadrilateral.
Diagonal: The line segment joining any two opposite sides of a quadrilateral is called diagonal of the quadrilateral.
Properties of a Quadrilateral:
In a quadrilateral, there are 4 interior angles. The sum of these 4 angles is 3600.
⇒ the sum of the angles in a quadrilateral ABCD = 3600
i.e., ∠A + ∠B+ ∠C + ∠D = 3600
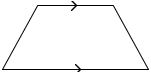
Trapezium: In a quadrilateral one pair of opposite sides are parallel, then it is called Trapezium.
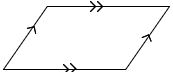
Parallelogram: In a quadrilateral two pair of opposite sides are parallel, then it is called a parallelogram.
Properties of parallelogram:
1.Opposite sides and opposite angles are equal.
2.Diagonals are bisected each other and not equal in length.
3.A diagonal of a parallelogram divides it into two congruent triangles.
Rectangle: In a parallelogram one of the angles is a right angle, then it is called Rectangle.
Properties of Rectangle:
1.Opposite sides are equal.
2.Each angle is 900
3.Diagonals are bisected each other and equal in length.
A diagonal of a parallelogram divides it into two congruent triangles.
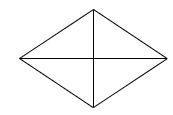
Rhombus: In a parallelogram two adjacent sides are equal, then it is called Rhombus.
Properties of Rhombus:
1.All sides are equal.
2.Opposite angles are equal.
3.Diagonals are bisected each other perpendicularly and not equal in length.
Square: In a Rhombus one of the angles is 900, then it is called a square.
Properties of Square:
1.all sides are equal.
2.Each angle is 900
3.Diagonals are bisected each other and equal in length.
Mid-point theorem:
The line segment joining the midpoints of two sides of a triangle is parallel to the third side and half of it.
In ∆ABC, D, E are midpoints of side AB and AC ⇒DE ∥ BC and DE = ½ BC.
The converse of mid-point theorem:
The line drawn through the mid-point of one of the sides of a triangle and parallel to another side will bisect the third side.
9.STATISTICS
Data: The facts or figures which are numerical or collected with a definite purpose are called data.
Statistics: Extraction of meaning from the data is studied in a branch of mathematics is called statistics.
Primary data: The information was collected by an investigator with a defined objective, the data obtained is called Primary Data.
Ex: Heights of the students in a class, the population in a country etc.
Secondary data: The information collected from a source, which had already been recorded is called secondary data.
Ex: No. of obscenities in the last month (School attendance register).
Presentation of data: Once the data is collected, the investigator has to find out ways to present in the form which is meaningful, easy to understand and shows its main features at a glance.
Range: The difference between maximum and minimum observations in data is called Range of the data.
Un grouped Frequency distribution table:
The actual observations of the data are shown in the table with their frequencies is called Un frequency distribution table.
The data is tabulated by using the tally marks
Grouped Frequency distribution table:
Presenting the data in groups with their frequencies is called frequency distribution table.
MEASURES OF CENTRAL TENDENCY
Mean: Mean is the sum of the observations divided by the no. of observations.
Mean for ungrouped data:
If x1, x2, … in are n observations then
If x1, x2, … xn are n observations occurs f1, f2, … fn times respectively then
Mean by deviation method:
where a = assumed mean.
di = xi – a (deviation)
Median:
Median is the middlemost observation of a given data.
First, we arrange the given data into ascending order.
If n is odd then median =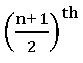 observation
observation
Mode:
The mode is the value of the observation which occurs most frequently.
Observation with the maximum frequency is called mode.
PDF Files || Inter Maths 1A &1B || (New) 6th maths notes|| TS 6 th class Maths Concept |
TS IX CLASS MATHS CONCEPT
10. SURFACE AREA AND VOLUMES
2 – D objects: The objects which have length and breadth are called two-dimensional figures (2 – D objects).
3 – D objects or Solids: The objects which have length, breadth and also height are called three-dimensional figures (3 – D objects).
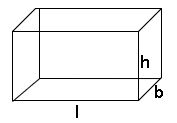
Cuboid:
Lateral surface area (L.S.A) = 2h (l + b) square units.
Total surface area (T.S.A) = 2 (lb + bh + hl) square units.
Volume = lbh cubic units.
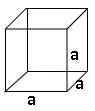
Cube:
Lateral surface area (L.S.A) = 4 a2 square units.
Total surface area (T.S.A) = 6 a2 square units.
Volume = a3 cubic units.
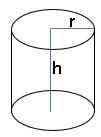
Cylinder:
Curved surface area (C.S.A) = 2πrh square units.
Total surface area (T.S.A) = 2πr (r +h) square units.
Volume = πr2 h cubic units.
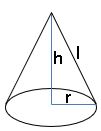
Cone:
Curved surface area (C.S.A) = πrl square units.
Total surface area (T.S.A) = πr (r +l) square units.
Volume = πr2 h cubic units.
Sphere:
Total surface area (T.S.A) = 4πr2 square units.
Volume = πr3 cubic units.
Hemisphere:
Curved surface area (C.S.A) = 2πr2 square units.
Total surface area (T.S.A) = 3πr2 square units.
Volume = πr3 cubic units.
11.AREAS
Planar region:
The part of the plane enclosed by a simple closed figure is called a planar region corresponding to that figure.
Area:
The magnitude or measure of the planer region corresponding to the figure is called its area. The area of a figure is a number associated with the part of the plane enclosed by the figure.
The unit area is the area of a square of a side of unit length.
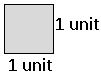 This is defined as 1 square unit
This is defined as 1 square unit
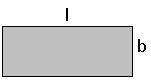
∎ The area of the rectangle whose length ‘l’ and breadth ‘b’ is l × b square units.
∎ The areas of two congruent figures are equal. If two figures have the same area, they need not be congruent.
∎ parallelograms on the same base and between the same parallel are equal in area.
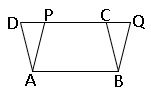
Parallelograms ABCD and ABQP have same base AB and lie between the parallel sides AB and QD
∴ Area of parallelogram ABCD = Area of parallelogram ABQP.
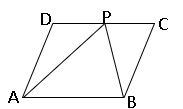
∎ If a triangle and parallelogram have the same base and lies between the parallel lines, then the area of the triangle is equal to half of the area of the parallelogram.
Area of the triangle APB = ½ (Area of the parallelogram ABCD)
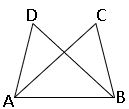
∎ If two triangles same base and lies between the parallel lines, then areas of triangles are equal.
Area of ∆ABC = Area of ∆ABD.
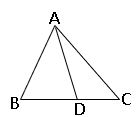
∎ The median of the triangle divides it into two triangles of equal area.
Area of ∆ABD = Area of ∆ADC.
12. CIRCLES
Circle:
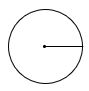
A circle is a collection of all points in a plane that are at a constant distance from a fixed point on the plane.
The fixed point is called the centre of the circle and the constant distance is called the radius of the circle.
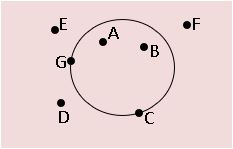
∎ A circle divides the plane into three parts: (i) inside the circle (interior of the circle) (ii) on the circle (iii) outside the circle (exterior of the circle).
Points A, B are the interior of the circle
Points G, C are on the circle
Points D, E and F are exterior of the circle
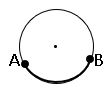
Chord: A line segment joining any two points on the circle is called a chord of the circle.
AB is the chord
Arc: The part of the circle between ant two points on it is called Arc of the circle.
If the arc is smaller than the semicircle, then it is called ‘minor arc’
If the arc is greater than the semicircle, then it is called ‘major arc’
Segment:
The region between the chord and the minor arc is called the minor segment.
The region between the chord and the major segment is called the major segment.
Sector:
The area enclosed by an arc and the two radii joining the centre to the endpoints of an arc is called a sector.
∎ Equal chords of a circle subtend equal angles at the centre.
∎ If the angle subtended by the chords of a circle at the centre are equal, then the chords are equal.
∎ The perpendicular from the centre of the circle to a chord bisects the chord.
∎ If a line drawn from the centre of the circle bisects the chord then the line is perpendicular to that chord.
∎ There is one and only one circle that passes through three non-collinear points.
∎ Arcs of Equal length subtend equal angles at the centre.
∎ The angle subtended by an arc at the centre is twice the angle subtended by it on the remaining arc of the circle.
∎ The angle subtended by an arc in the same segment is equal.
∎ If a line segment joining two points, subtends an equal angle at two other points lying on the same side of the line then the four points lie on a circle.
Concyclic points:
The points which lie on the same circle are called concyclic points.
Cyclic quadrilateral:
If the vertices of a quadrilateral lie on the same circle, then it is called a cyclic quadrilateral.
∎ The pairs of opposite angles of an acyclic quadrilateral are supplementary.
∎ If the sum of any pair of opposite angles in a quadrilateral is 1800, then the quadrilateral is cyclic.
13. GEOMETRICAL CONSTRUCTIONS
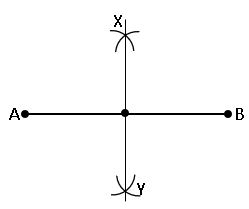
To construct the perpendicular bisector of a given line segment:
Steps of construction:
Step – 1: Draw a line segment of AB.
Step – 2: Taking A as the centre with a radius more than half of AB, draw an arc on either side of the line segment AB.
Step – 3: Taking B as the centre, with the same radius as above, draw arcs so that they intersect the previously drawn arcs.
Step – 4: Marks the points of intersection as X and Y.
Step – 5: Join X and Y, then XY is the perpendicular bisector of AB.
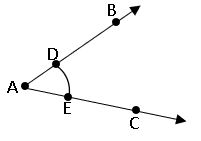
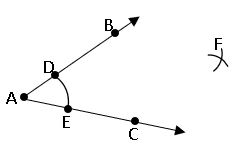
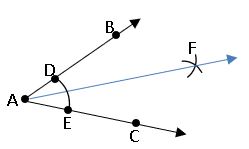
To construct the bisector of a given angle:
Steps of construction:
Step – 1: Draw the given ∠BAC.
Step – 2: Taking A as the centre with any radius, draw an arc to intersect the rays AB and AC at D and E respectively.
Step – 3: Taking D and E as the centres, draw two arcs with equal radii to intersects each other at F.
Step – 4: Draw a ray AF. It the bisector of ∠BAC.
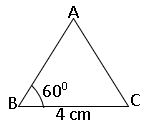
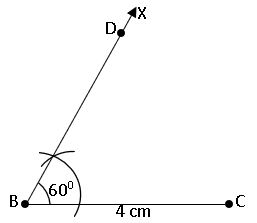
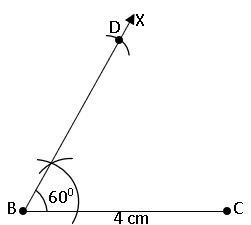
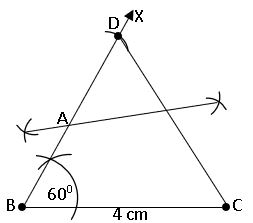
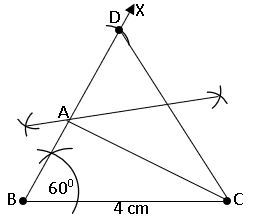
To construct a triangle, given its base, a base angle and sum of the other two sides:
construct a triangle ABC, BC = 4cm, AB + BC = 6cm and ∠B = 600
Steps of construction:
Step – 1: Draw a rough sketch of ∆ABC.
Step – 2: Draw the base BC = 4cm and construct ∠CBX = 600 at B.
Step – 3: With centre B and radius 6cm (AB + BC = 6cm) draw an arc on BX to meet at D.
Step – 4: Join CD and Draw the perpendicular bisector of CD to BD at A.
Step – 5: Join A to C get the required triangle ABC.
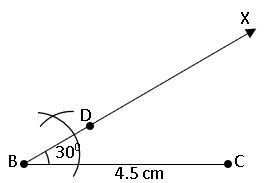
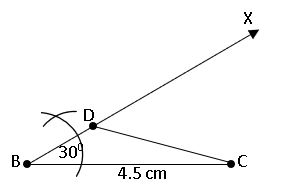
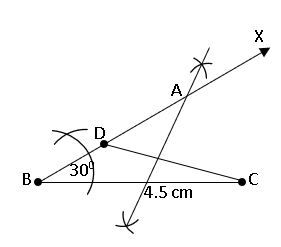
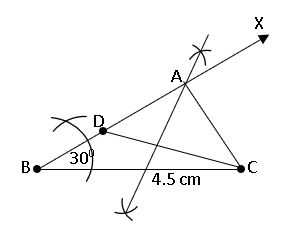
To construct a triangle, given its base, a base angle and difference of the other two sides:
construct a triangle ABC, BC = 4.5cm, AB – AC = 1.5cm and ∠B = 300
Steps of construction:
Step – 1: Draw a rough sketch of ∆ABC.
Step – 2: Draw the base BC = 4.5cm and construct ∠CBX = 300 at B.
Step – 3: With centre B and radius 1.5cm (AB – AC = 1.5cm) draw an arc on BX to meet at D.
Step – 4: Join CD and Draw the perpendicular bisector of CD to BD at A.
Step – 5: Join A to C get the required triangle ABC.
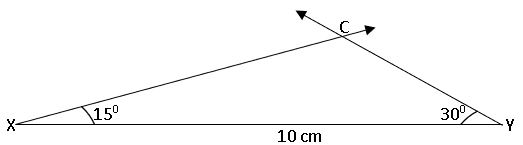
To construct a triangle, given its perimeter and its two base angles:
Construct triangle ABC, in which ∠A = 600, ∠B = 300 and AB + BC + CA = 10cm.
Steps of construction:
Step – 1: Draw a rough sketch of ∆ABC.
Step – 2: Draw a line segment XY = 10 cm.
Step – 3: Construct ∠YXC = 150 and ∠XYC = 300 which are angular bisectors of ∠B and ∠A respectively and they meet at C.
Step – 4: Draw the perpendicular bisectors of CX and CY to intersect XY At B and A respectively.
Step – 5: Join BC and AC, ∆ABC is the required triangle.
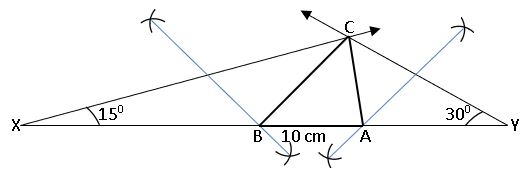
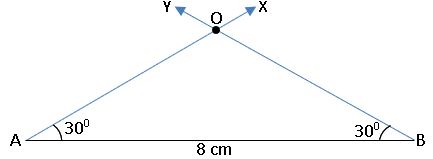
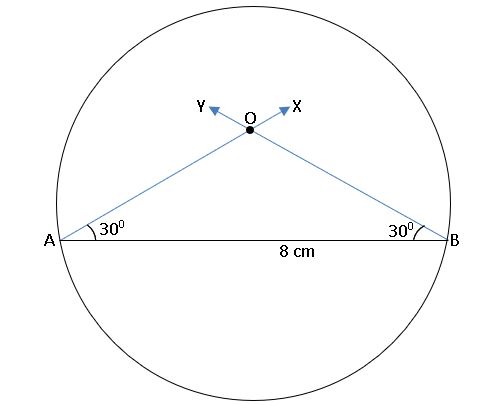
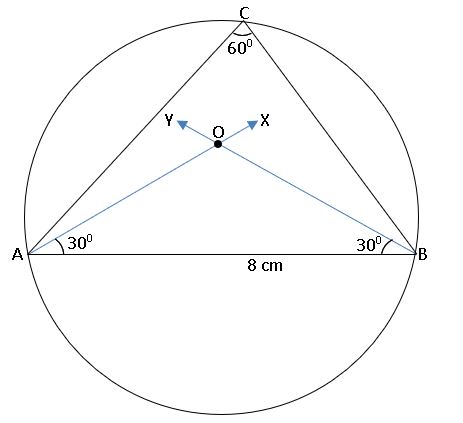
To construct a circle segment given a chord and given an angle:
Construct a segment of a circle on a chord of length 8 cm and containing the angle of 600
Step – 1: Draw a rough sketch of ∆ABC.
Step – 2: Draw a line segment AB = 8 cm.
Step – 3: Draw a ray AX such that ∠BAX = 300 and draw ray BY such that ∠ABY = 300
Step – 4: With centre ‘O’ and radius OA or OB, draw the circle.
Step – 5: Mark a point C on the arc of the circle. Join AC and BC. We get ∠ACB = 600
14. PROBABILITY
Random Experiment: If in an experiment all the possible outcomes are known in advance and none of the outcomes can be predicted with certainty, then such an experiment is called a random experiment.
Ex: Throwing a die, Tossing A coin.
Events: The possible outcomes of a trial are called events.
To measure the chance of its happening numerically we classify them as follows:
Certain: Something that must happen
Equally likely: something that has the same chance of occurring.
Less likely: Something that would occur with less chance.
More likely: Something that would occur with more chance.
Impossible: Something that cannot happen.
ix Class Maths
15. PROOFS IN MATHEMATICS
Statements: The sentences that can be judged to be true or false but not both are called statements. The mathematical statements are cannot be ambiguous.
Hypothesis: A statement of an idea that explains a sense of observation is called Hypothesis.
Mathematical proof: A process that can establish the truth of a mathematical statement based purely on logical arguments is called mathematical proof.
Conjecture: The statements which are neither proved nor disproved are called Conjecture.
Axiom: The statements which are assumed to be without proof are called axioms.
Theorem: A mathematical statement whose truth has been established or proved is called Theorem.
Proof: A proof is made up of a successive sequence of mathematical statements.
Deductive reasoning: The logical reasoning which is used in the establishment of the truth of an unambiguous statement is called Deductive reasoning.
Inductive reasoning: The reasoning which is based on examining of variety of cases discovering pattern and forming conclusion is called inductive reasoning.
ix Class Maths
- TS 6th Maths Concept
- TS 7th Maths Concept
- TS 8th Maths Concept
- TS 9th Maths Concept
- TS 10th Maths Concept
Visit my Youtube Channel: Click on Below Logo