11th Class Maths: This note is designed by ‘Basics in Maths’ team. These notes to do help the CBSE 11th class Maths students fall in love with mathematics and overcome their fear.
These notes cover all the topics covered in the CBSE 11th class Maths syllabus and include plenty of formulae and concept to help you solve all the types of11thMath problems asked in the CBSE board and entrance examinations.
1. SETS
Well-defined objects:
- All objects in a set must have the same general similarity or property.
- Must be able to confirm whether something belongs to the set or not.
Set: – A collection of well-defined objects is called a set.
∗ Sets are usually denoted by capital English alphabets like A, B, C, and so on.
∗ The elements in set are taken as small English alphabets like a, b, c, and so on.
∗ Set theory was developed by George canter.
• If any object belongs to a set, then it is called an object/element. We denote by ∈ to indicate that it belongs to. If it does not belong to the set then it is denoted by ∉.
Ex: – 1 ∈ N, 0 ∈ W, −1 ∈ Z, 0 ∉ N, etc.
Methods of representing sets:
Roster or table or listed form: –
In this form all the elements of the set are listed, and the elements are separated by commas and enclosed within braces { }.
Ex: – set of vowels in English alphabet = {a, e, I, o, u},
set of even natural numbers less than 10 = {2, 4, 6, 8} etc.
Note: – In roster form, an element is not repeated. We can list the elements in any order.
Set builder form:
Pointing an element in a set to x (or any symbols such as y, z, etc.) followed by a colon(:), next to write the properties or properties of the elements in that set and placed in flower brackets is called the set builder form.: Or / symbols read as ‘such that’
Ex: – {2, 4, 6, 8} = {x / x is an even and x ∈N, x< 10},
{a, e, i, o, u} = {x : x is a vowel in English alphabet}.
Null set: – (empty set or void set) the set which has no elements is called as a null set. It is denoted by ∅ or { }.
Finite and infinite sets: – If a set contains a finite no. of elements then it is called a finite set. If a set contains an infinite no. of elements then it is called an infinite set.
Ex: – A = {1, 2,3, 4} → finite set
B = {1, 2, 3, 4….}
Equal sets: – two sets A and B are said to be equal sets if they have the same elements., and write as A = B
Ex: – A = {1, 2, 3, 4}, B = {3, 1, 4, 2}
⟹ A = B.
Subset: – for any two sets A and B, if every element of set A is in set B, then we can say that A is a subset of B. It is denoted by A ⊂ B.
Ex: – If A = {1, 2, 3, 4, 5, 6, 7, 8}, subsets of A are {1}, {1, 3, 5}, {1,2,3,4}, and so on.
Power set: – set of all the subsets of a set A is called the power set of A. It is denoted by p(A).
Ex: – A = {1,2,3}
P(A) = {{1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1, 2, 3}, ∅}.
Intervals:
∗ Open interval: – (a, b) = {x: a< x <b} → set of rational numbers lies between a and b.
∗ Closed interval: – [a, b] = {x: a≤ x ≤b} → set of rational numbers lies between a and b, including a and b.
∗ Open – closed: – (a, b] = {x: a< x ≤b} → set of rational numbers lies between a and b, excluding a and including b.
∗ Closed-open: -[a, b) = {x: a≤ x <b} → set of rational numbers lies between a and b, including a and excluding b.
Universal set: – A set that contains all the subsets of it under our consideration is called a universal set.
Cardinal number of a set: – Number of elements in a set A is called the cardinal number of that set A. It is denoted by n(A).
• If a set has n elements, then no. of elements of that set has 2n
Equivalent sets: – two set A and B are said to be equivalent sets if n(A) = n(B) (they have the same cardinal number).
Ex: – A = {1, 2, 3}, B = {a, b, c}
n(A) = 3 and n(B) = 3
∴ A = B.
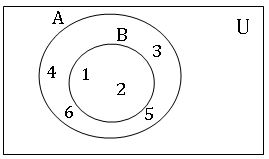
Venn diagrams:
U = {1, 2, 3, 4, 5, 6}
the relationship between sets is usually represented by means of diagrams which are known as ‘Venn diagrams. These diagrams consist of rectangles and circles. A universal set is represented by rectangles and subsets by circles.
U = {1, 2, 3, 4, 5, 6} A = {1, 2, 3} B = {1, 2}
Visit my Youtube Channel: Click on Below Logo