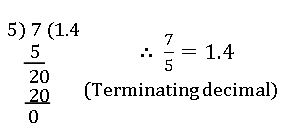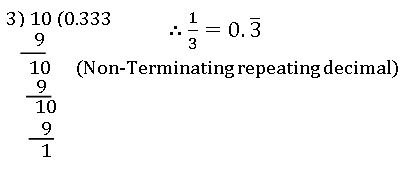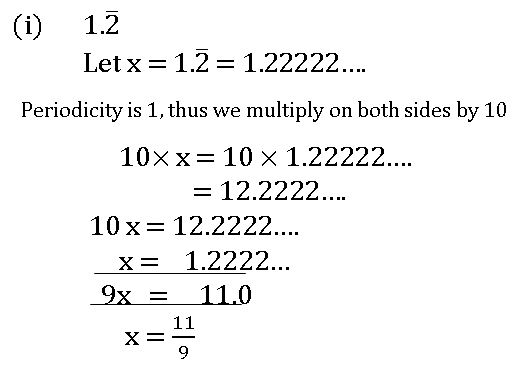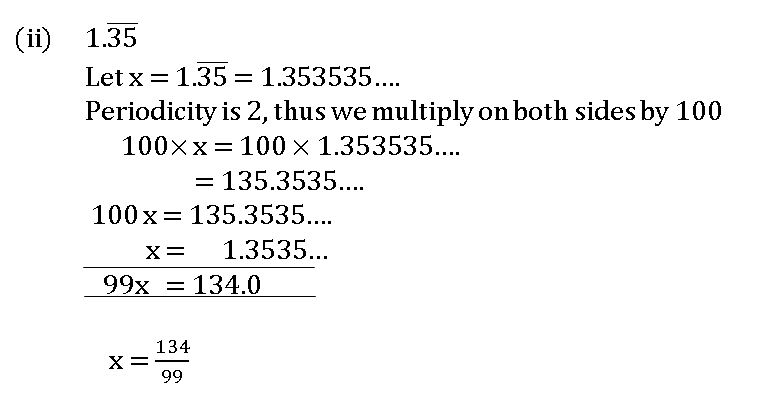ICSE IX CLASS MATHS CONCEPT FEATURE IMAGE

ICSE IX Class Maths Concept

By

ICSE IX Class Maths Concept

 

ICSE IX Class Maths Concept: This note is designed by the ‘Basics in Maths’ team. These notes to do help the ICSE 9th class Maths students fall in love with mathematics and overcome their fear.

These notes cover all the topics covered in the ICSE 9th class Maths syllabus and include plenty of formulae and concept to help you solve all the types of ICSE 9th

Math problems are asked in the CBSE board and entrance examinations.

1. RATIONAL AND IRRATIONAL NUMBERS

Natural numbers: counting numbers 1, 2, 3… called Natural numbers. The set of natural numbers is denoted by N.

N = {1, 2, 3…}

Whole numbers: Natural numbers including 0 are called whole numbers. The set of whole numbers denoted by W.

W = {0, 1, 2, 3…}

Integers: All positive numbers and negative numbers including 0 are called integers. The set of integers is denoted by I or Z.

Z = {…-3, -2, -1, 0, 1, 2, 3…}

Rational number: The number, which is written in the form of, where p, q are integers and q ≠ o is called a rational number. It is denoted by Q.

∗ In a rational number, the numerator and the denominator both can be positive or negative, but our convenience can take a positive denominator.

Ex: – \inline \fn_jvn -\frac{2}{3} can be written as \inline \fn_jvn \frac{-2}{3}=\frac{2}{-3}  but our convenience we can take \inline \fn_jvn \frac{-2}{3}

Equal rational numbers:

For any 4 integers a, b, c, and d (b, d ≠ 0), we have \inline \fn_jvn \frac{a}{b}=\frac{c}{d} ⇒ ad = bc

The order of Rational numbers:

If  are two rational numbers such that b> 0 and d > 0 then \inline \fn_jvn \frac{a}{b}> \frac{c}{d} ⇒ ad > bc

The absolute value of rational numbers:

The absolute value of a rational number is always positive. The absolute value of  \inline \fn_jvn \frac{a}{b} is denoted by \inline \fn_jvn \left | \frac{a}{b} \right | .

Ex: – absolute value of \inline \fn_jvn -\frac{2}{3}=\frac{2}{3}

To find rational number between given numbers:

  • Mean method: – A rational number between two numbers a and b is \inline \dpi{120} \fn_jvn \frac{a + b}{2}

  Ex: – insert two rational number between 1 and 2

1 <  \inline \dpi{120} \fn_jvn \frac{1 + 2}{2} < 2   ⟹     1 <  \inline \dpi{120} \fn_jvn \frac{3}{2}  < 2

1 <  \inline \dpi{120} \fn_jvn \frac{3}{2} \inline \dpi{120} \fn_jvn < \frac{\frac{3}2{+2}}{2}< 2   ⟹   1 < \inline \dpi{120} \fn_jvn \frac{3}{2}< \frac{7}{4} \dpi{120} \fn_jvn <  2

To rational numbers in a single step: –

Ex:- insert two rational numbers between 1 and 2

To find two rational numbers, we 1 and 2 as rational numbers with the same denominator 3

(∵ 1 + 2 = 3)

1 =   \fn_jvn \frac{1\times 3}{3}  and 2 = \inline \dpi{120} \fn_jvn \frac{2\times 3}{3}

\inline \dpi{120} \fn_jvn \frac{3}{3}\left ( 1 \right )< \frac{4}{3}< \frac{5}{3}< \frac{6}{3}\left ( 2 \right )

 

Note: – there are infinitely many rational numbers between two numbers.

The decimal form of rational numbers

icse ix terminating desimals

icse ix class nomterminating repeating decimal form

∗ Every rational number can be expressed as a terminating decimal or a non-terminating repeating decimal.

Converting decimal form into \dpi{120} \fn_jvn \frac{p}{q}  the form:

1. Terminating decimals: –

1.2 =\inline \dpi{120} \fn_jvn \frac{12}{10}=\frac{6}{5}

1.35 =\inline \dpi{120} \fn_jvn \frac{135}{100}=\frac{27}{20}

2. Non-Terminating repeating decimals: –

CONVERT INTO PB Y Q FORM 1

CONVERT INTO P BY Q FORM 2

Irrational numbers:

  • The numbers which are not written in the form of  \dpi{120} \fn_cm \frac{p}{q}, where p, q are integers, and q ≠ 0 are called rational numbers. Rational numbers are denoted by QI or S.
  • Every irrational number can be expressed as a non-terminating decimal or non-repeating decimal.

Ex:- \dpi{120} \fn_cm \sqrt{2},\, \sqrt{5},\pi and so on.

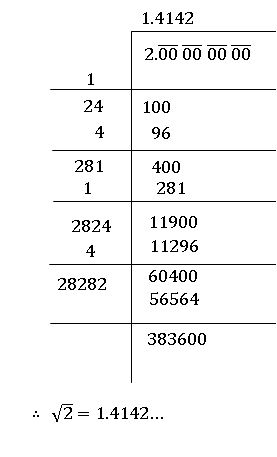
  • Calculation of square roots:
  • There is a reference of irrationals in the calculation of square roots in Sulba Sutra.
  • Procedure to finding \dpi{120} \fn_cm \sqrt{2} value:

finding sqrt of 2

Visit my Youtube Channel: Click on Below Logo

AS_Tutorioal_Png

Related Posts

Scroll to Top