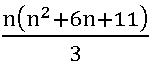Ch. 2 Mathematical Indunction Exerxise Solutions

Mathematical Indunction (M.I) Exerxise wise Solutions

Mathematical Indunction: It is a technique for proving results or establishing statements for natural numbers. This part illustrates the method through a variety of examples.

Definition:
Mathematical Induction  is a mathematical technique which is used to prove a statement, a formula or a theorem is true for every natural number.

The technique involves steps to prove a statement, as stated below −
Let P(n) or S(n) be the given statement

Step 1: For n =1
                 we get LHS = RHS
                 then P(n) is true for n= 1
Step 2: Let us assume thet P(n) is true for n =k
Step 3: We have to Prove P(n) is true for n= k + 1

Laplace:

Laplace was a mathematecian and astronomer whose work was pivotal to the development of mathematical astronomy. His most outstanding work was done in the fields of celestial mechonics, probability, differential equations, and geodesy. His five volume work on celestial mechonics earned him the title of the Newton of France.

“Analysis and natural philosophy owe their most important discoveries to this fruitful means, which is called indunction” – Pierr Simon de Laplace

Exercise 2(a)

Using Mathematical Indunction, Prove each of the following statement for all n ∈ N.

1. 1² + 2² + 3² + …… + n²=

Let p(n) be the given statement that

 1² + 2² + 3² + …… + n²=

For n= 1

LHS = 1² = 1

RHS = =  = 1

LHS = RHS

P(n) is true for n = 1

Let us assume that P(n) is true for n = k

i.e., 1² + 2² + 3² + …… + k²=  ………… (1)

for n = k + 1

add (k +1)² on both sides of (1)

1² + 2² + 3² + …… + k² + (k +1)² = 

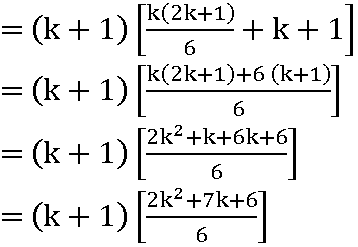
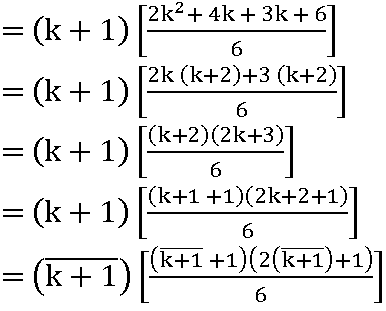
P(n) is true for n = k+ 1

∴ By the principle of  M.I.  P(n) is true for all n ∈ N

∴ 1² + 2² + 3² + …… + n²=

2.  2.3 + 3.4 + 4.5 + ……… up to n terms =

First factors of given series are: 2, 3, 4, 5, …

                                  a = 2, d = 1

                                 a_n = a + (n – 1) d

                                       = 2 + (n – 1) (1)

                                       = 2 + n – 1

                                       = n + 1

Second factors of given series are: 3, 4, 5,…

                                  a = 3, d = 1

                                 a_n = 3 + (n – 1) d

                                       = 3 + (n – 1) (1)

                                       = 3 + n – 1

                                       = n + 2

n^th term of given series is (n + 1) (n + 2)

let P(n) be the given statement that

2.3 + 3.4 + 4.5 + ……… + (n + 1) (n + 2) =

For n = 1

LHS = 2.3 = 6

RHS =  =  =  = 6

LHS = RHS

P(n) is true for n = 1

Let us assume that P(n) is true for n = k

i.e., 2.3 + 3.4 + 4.5 + ……… + (k + 1) (k + 2) =  ………… (1)

for n = k + 1

  add (k + 2) (k + 3) on both sides of (1)

 2.3 + 3.4 + 4.5 + ……… + (k + 1) (k + 2) + (k + 2) (k + 3)  

  =  + (k + 2) (k + 3)

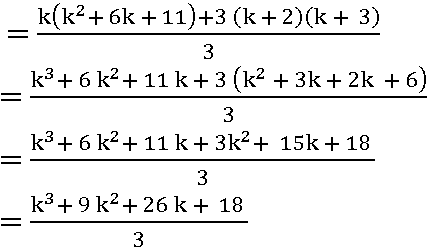
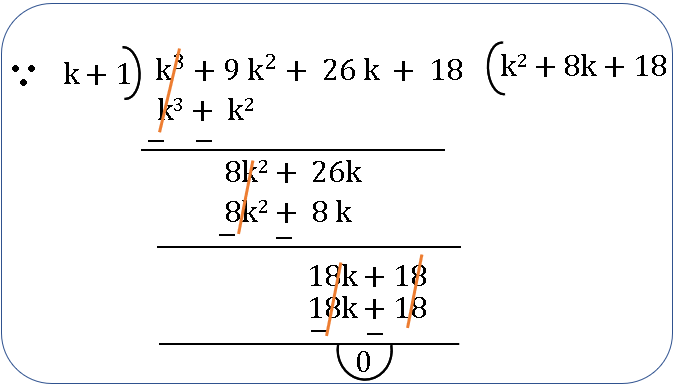
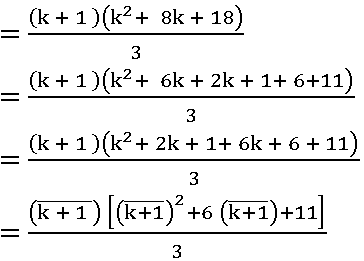
P(n) is true for n = k+ 1

∴ By the principle of  M.I. 

   P(n) is true for all n ∈ N

∴ 2.3 + 3.4 + 4.5 + ……… up to n terms =

3 . 

Sol:

let P(n) be the given statement that

       For n = 1

        LHS =  =

        RHS =  =  =

       LHS = RHS

       P (n) is true for n = 1

Let us assume that P(n) is true for n = k

  ………… (1)

For n = k + 1

Add on both sides of (1)

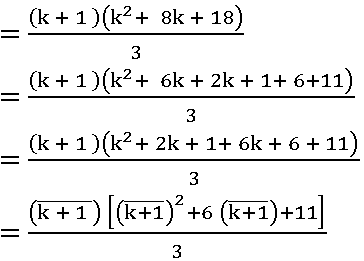
P (n) is true for n = k + 1

∴ By the principle of M.I.   P(n) is true for all n ∈ N

∴   

4. 4³ + 8³ + 12³ + … up to n terms = 16 n² (n + 1)²

Sol:

let P(n) be the given statement that

 4, 8, 12, … are in AP

a = 4, d = 4

a_n = a + (n – 1) d

     = 4 + (n – 1)4

     = 4 + 4n – 4

      = 4n

n^th term of given series is (4n)³

let P(n) be the given statement that

4³ + 8³ + 12³ + … + (4n)³= 16 n² (n + 1)²

       For n = 1

        LHS = 4³ = 63

        RHS = 16 (1)² (1 + 1)² = 16 × 4 = 64

       LHS = RHS

       P (n) is true for n = 1

      Let us assume that P(n) is true for n = k

4³ + 8³ + 12³ + … + (4k)³= 16 k² (k + 1)² ………… (1)

      For n = k + 1

     Add [4 (k + 1)]³ on both sides of (1)

    4³ + 8³ + 12³ + … + (4k)³= 16 k² (k + 1)² + [4 (k + 1)]³

                                                      = 16 k² (k + 1)² + 64 (k + 1)³

                                                      = 16 (k + 1)² [k² + 4 (k + 1)]

                                                      = 16 (k + 1)² [k² + 4 k + 4]

                                                      = 16 (k + 1)² (k + 2)²

                                                      = 16 (k + 1)² ( + 1)²

P (n) is true for n = k + 1

∴ By the principle of Mathematical induction

   P(n) is true for all n ∈ N

5. a + (a + d) + (a + 2d) + …. up to n terms =

Sol:

Given series is a + (a + d) + (a + 2d) + …. up to n terms =

n^th term of the given series is a + (n – 1) d

     let P(n) be the given statement that

      a + (a + d) + (a + 2d) + …. +[a + (n – 1) d] =

     for n = 1

     LHS = a;     RHS = = a

     LHS = RHS

     P(n) is true for n = 1

     Let us assume that p(n) is true for n = k

   a + (a + d) + (a + 2d) + …. + [a + (k – 1) d] = ……. (1)

   add (a + k d) on both sides of (1)

    a + (a + d) + (a + 2d) + …. [a + (k – 1) d] + [a + kd] = + [a + kd]

P (n) is true for n = k + 1

∴ By the principle of Mathematical induction

   P(n) is true for all n ∈ N

Mathematical Induction

Visit my Youtube Channel: Click on Below Logo