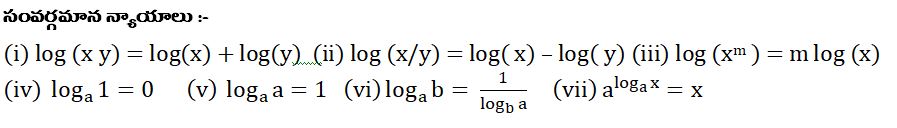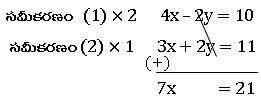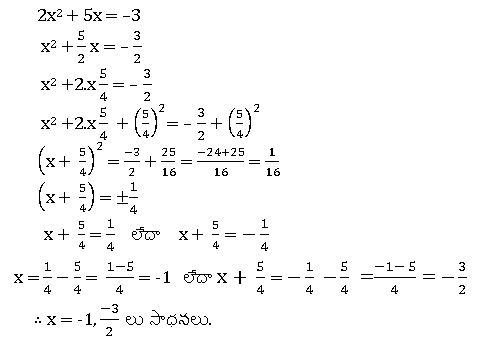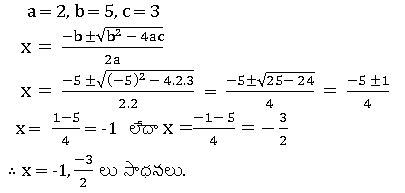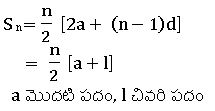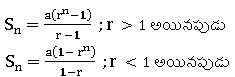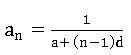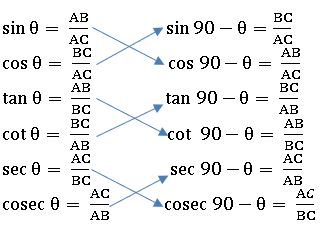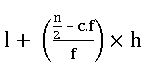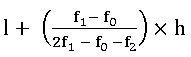10 వ తరగతి గణితం నోట్స్
10 వ తరగతి గణితం
10 వ తరగతి గణిత శాస్త్రాన్ని అధ్యయనం చేయడం అంటే, పిల్లలు తమ స్వంత అభ్యాసానికి బాధ్యత వహిస్తారు మరియు సమస్యలను పరిష్కరించడానికి భావనలను వర్తింపజేయడం నేర్చుకుంటారు.
ఈ విషయం . ఈ గమనికలు విద్యార్థులకు గణితంను ఇస్టపడేలా మరియు భయాన్ని అధిగమించడానికి సహాయపడతాయి.
1. వాస్తవ సంఖ్యలు
మనం ముందు తరగతులలో వివిధ రకాలైన సంఖ్యలను గురించి తెలుసుకున్నాము .అంటే సహజ సంఖ్యలు, పూర్ణాంకాలు, పూర్ణ సంఖ్యలు, కరణీయ , అకరణీయ సంఖ్యలను గురించి నేర్చుకున్నాము .
అకరణీయ సంఖ్యలు : p,q లు పూర్ణ సంఖ్య లై , q ≠ 0 అయిన సందర్భం లో రూపం లో రాయగల సంఖ్య లను అకరణీయ సంఖ్యలు అంటారు . దీనిని Q తో సూచిస్తారు .
ఉదా :- మొదలగునవి.
కరణీయ సంఖ్యలు : రూపం లో రాయలేని సంఖ్యలను కరణీయ సంఖ్యలు అంటారు . దీనిని QI లేదా S తో సూచిస్తారు .
ఉదా :- మొదలగునవి.
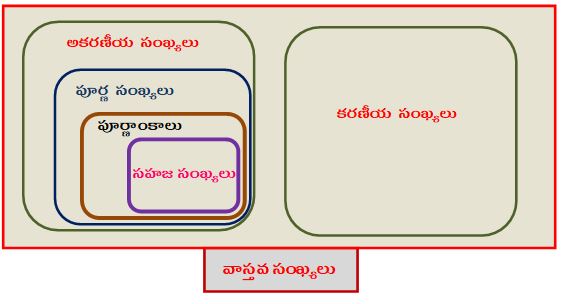
వాస్తవ సంఖ్యలు : అకరణీయ , కరణీయ సంఖ్యల సమూహాన్ని వాస్తవ సంఖ్యలు అంటారు .
కింది పటములో మనం వీటిని చూడ వచ్చు.
భాగహార శేష నిధి :
a, b అనే ధన పూర్ణాంకాలు ఇచ్చినప్పుడు a = b q + r, 0≤ r <b అయ్యే విధంగా ఏకైక జత పూర్ణాంకాలు q ,r లు వ్యవస్తితం అవుతాయి.
ఇది అందరికి తెలిసినప్పటికీ యూక్లిడ్ పుస్తకాల సంకలనం లోని 7 వ పుస్తకం లో మొట్టమొదటగా నమోదు చేయడం జరిగింది.
ఈ భాగహార శేషనిధి మీద యూక్లిడ్ భాగహార శేష నిధి ఆధారపడి ఉంది.
యూక్లిడ్ భాగహార శేషనిధి కేవలం ధన పూర్ణ సంఖ్యల పైనే నిర్వచించ బడినా , దానిని అన్ని శూన్యేతర పూర్ణ సంఖ్యలకు అనువర్తింప చేయవచ్చు .
యూక్లిడ్ భాగహార శేషనిధి ఉపయోగించి గ . సా . భా ను కనుక్కోవడం :
రెండు ధన పూర్ణ సంఖ్యల సామాన్య కారాణాంకాలలోని అతి పెద్ద కారణాo న్కాన్ని గ .సా. భా అంటారు .
ఉదా:- 9 , 24 ల గ . సా .భా కనుక్కోవడం
దీనిని 24 = 9×2 + 18 గా రాయవచ్చు
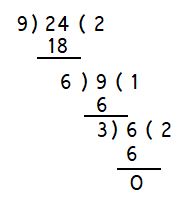
9 , 24 కన్నా పెద్దది కావున 24 ను 9 చే భాగిస్తే శేషం 6 వస్తుంది
పై దానిలో ని భాజకం 9 మరియు 6 పై యూక్లిడ్ న్యాయాన్ని అనువర్తింప చేయగా
9 = 6 ×1 + 3 గా రాయవచ్చు
పై దానిలో ని భాజకం 6 మరియు శేషం 3 పై యూక్లిడ్ న్యాయాన్ని అనువర్తింప చేయగా దానిని
6 = 3 ×2 + 0 గా రాయవచ్చు
పై దాని లో శేషం సున్నా వచ్చింది
కావున 9 , 24 ల గ . సా .భా 3 అవుతుంది.
ప్రాథమిక అంకగణిత సిద్ధాంతం :
ప్రతి సంయుక్త సఖ్యను ప్రదానానంకముల లబ్దంగా రాయవచ్చు మరియు ప్రధాన కారణాంకాల క్రమం ఏదైనప్పటికీ ఈ కారణాంకాల లబ్దం ఏకైకం .
ఒక సంయుక్త సంఖ్య x ను x = p 1 p 2 ….p n అని రాయవచ్చు . దీనిలో p 1 , p 2, …., p n ఆరోహణ క్రమం లో రాయబడిన ప్రధానాంకాలు , అంటే p 1≤ p 2 ≤….≤ p n.
ఈ సందర్భం లో ఒకే రకమైన ప్రదానంకములు వాడినచో వాటిని ప్రధానాంకాల ఘా తాoకాలుగా రాస్తాము . ఒకసారి మనం ఈ సంఖ్యలు ఆరోహణ క్రమంలో ఉన్నాయని భావిస్తే . అప్పుడు లబ్దం ఏకైకం .
ఉదా :- 360 = 3×3×2× 2 × 2 × 5 = 32 × 23 × 5
ప్రధాన కారణాంకాల లబ్ద పద్ధతి ద్వారా గా. సా . భా మరియు కా . సా . గు కనుక్కోవడం;
9 , 24 ల గ . సా .భా మరియు కా. సా . గు. కనుక్కోవడం
9 యొక్క ప్రధాన కారణాంకాలు = 3 × 3 = 32
24 యొక్క ప్రధాన కారణాంకాలు = 2 × 2 ×2 × 3 = 23 ×31
9 , 24 ల గ . సా .భా = 31 = 3 ( సంక్యల యొక్క సామాన్య కారణాంకంల కనిష్ఠ ఘాతాల లబ్ధం )
9 , 24 ల కా. సా . గు.= 32× 23 = 9×8 = 72 (సంఖ్యల యొక్క కారణాంకంల గరిష్ఠ ఘాతాల లబ్ధం)
అకరణీయ సంఖ్యలు మరియు వాటి దశాంశ రూపాలు :
x అనేది ఒక అకరణీయ సంఖ్య మరియు దీని ధశాంశ రూపం ఒక అంతమయ్యే దశాంశము ,అయినప్పుడు x ను p, q లు పరస్పర ప్రధా నాంకములు అయివున్న p /q రూపం లో వ్యక్త పరచవచ్చు . మరియు q యొక్క ప్రధాన కారాణాంకాల లబ్దం 2m 5 n అగును , n ,m లు ఋణేతర పూర్ణ సంఖ్యలు .
పై దాని విపర్యయం ఇలా ఉంటెుంది
• n ,m లు ఋణేతర పూర్ణ సంఖ్యలు మరియు q యొక్క ప్రధాన కారాణాంకాల లబ్దం 2m 5 n కలిగినటువంటి అకరణీయ సంఖ్య x = p /q అయిన, xయొక్క ధశాంశ రూపం ఒక అంతమయ్యే దశాంశము అగును ,
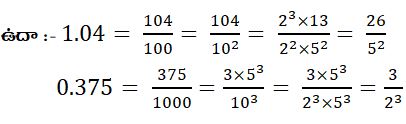
• n ,m లు ఋణేతర పూర్ణ సంఖ్యలు మరియు q యొక్క ప్రధాన కారాణాంకాల లబ్దం 2m 5 n రూపంలో లేకుంటే , అకరణీయ సంఖ్య x = p /q అయిన, xయొక్క ధశాంశ రూపం ఒక అంతంకాని దశాంశము అగును.
ఉదా :-
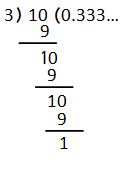
కరణీయ సంఖ్యలు :-
• p, q లు కరణీయ సంఖ్యలు మరయు q ≠ 0 అయిన p /q రూపం లో రాయలేని సంఖ్యలను కరణీయ సంఖ్యలు అంటారు .
• ప్రతీ కరణీయ సంఖ్య ధశాంశ రూపం ఒక అంతంకాని దశాంశము అగును.
ప్రవచనం: p అనేది ఒక ప్రధాన సంఖ్య మరియు a ఒక ధనపూర్ణ సంఖ్య అయితే “ a2 ను p నిశ్శేషంగా భాగిస్తే a ను p నిశ్శేషంగాభాగిస్తుంది.
ఘాతాలు :
• a n ను ఘాతాంక రూపం అంటాము. a ను భూమి అని , n ను ఘాతము అని అంటారు.
(i) (ii)
(iii) ( am)n = amn (iv) a0 = 1
సంవర్గమానాలు:-
x మరియు aలు ధనపూర్ణసంఖ్యలై a ≠1 అయివుండి ax = n అయిన x = అగును.
2. సమితులు
• గణిత పరిశోధనలలో సమితి వాదాన్ని ‘ జార్జి కాంటర్’ అభివృద్ధి పరిచారు.
సమితి: సునిర్విచిత వస్తువుల సముదాయాన్ని సమితి అంటారు.
• సునిర్విచితం అనగా :
1 . సమితిలోని వస్తువులన్నిటికి ఒకే విధమైన సామాన్య పోలిక లేదా ధర్మం కలిగి ఉండాలి .
2 . ఏదైనా ఓకే సమితికి చెందినది, లేనిది నిర్దారించే టట్లు ఉండాలి.
• సమితి పేరును ఇంగ్లీష్ వర్ణమాల లోని పెద్ద అక్షరాలతో సూచిస్తారు. ఉదాహరణకు A, B, … మొదలగునవి.
• ఏదైనా ఓకే వస్తువు ఒక సమితికి చెందితే దాన్ని వస్తువులు/ మూలకాలు అంటారు . చెందినది (belongs to) అని తెలపటానికి మనం ∈ గుర్తు తో సూచిస్తాము.సమితికి చెందినది అయితే దానిని ∉ చే సూచిస్తాము.
• జాబితా రూపం లేదా రోస్టర్ రూపం : సమితికి చెందిన మూలకాలన్నిటిని ‘కామ’ (,) తో వేరు చేసి ప్లవర్ బ్రాకెట్ { } లో ఉంచితే వచ్చే రూపాన్ని జాబితా రూపం లేదా రోస్టర్ రూపం అంటారు.
ఉదా :- A = {1, 2, 3, 4}, B = { a, e, I, o, u}.
• సమితి నిర్మాణ రూపం లేదా లాక్షణిక రూపం : సమితి లోని మూలకాన్ని x ( లేక y, z మొదలగు ఏవైన గుర్తులు ) గా సూచించి , x ప్రక్కన : లేదా / (colon ) ఉంచి ఆ సమితి కి చెందిన మూలకాల యొక్క లక్షణాలు లేదా ధర్మాలను రాసి ప్లవర్ బ్రాకెట్ { } ఉంచితే వచ్చే రూపాన్ని సమితి నిర్మాణ రూపం లేదా లాక్షణిక రూపం అంటారు . : లేదా / గుర్తులను such that అని చదువుతాము .
ఉదా :- A = { x/ x ఒక సరి సంఖ్య మరియి x ∈N }, B = { y : y ఒక ప్రధాన సంఖ్య మరియు x < 10 }.
సమితులు – రకాలు
శూన్య సమితి : ఎలాంటి మూలకాలు లేని సమితిని శూన్య సమితి అంటారు. దీనిని { } లేదా ∅ చే సూచిస్తాము.
ఉదా:- ∅ = { x / x ఒక సహజ సంఖ్య మరియు 2 < x < 3 }.
పరిమిత సమితి : ఒక సమితిలోని మూలకాలను లెక్కించుటకు వీలైనచో ఆ సమితిని పరిమిత సమితి అంటారు.
ఉదా :- A = { ఒక పాటశాలలోని విద్యార్థులు }, B = { 1, 2, 3, 4 }.
అపరిమిత సమితి : ఒక సమితిలోని మూలకాలను లెక్కించుటకు వీలు కానిచో ఆ సమితిని అ పరిమిత సమితి అంటారు.
ఉదా :- A = { ఒక సరళ రేఖ పై ఉన్న బిందువులు }, B = { 1, 2, 3, 4,…….. }.
కార్డినల్ సంఖ్య : ఒక సమితి లోని మూలకాల సంఖ్యను తెలిపే దానిని ఆ సమితికి ‘కార్డినల్ సంఖ్య ‘ అంటారు. సమితి A యొక్క కార్డినల్ సంఖ్యను n(A ) చే సూచిస్తారు.
ఉదా :– A = { 1, 2 , 3, 4 } ⟹ n(A ) = 4
గమనిక :- శూన్య సమితిలో మూలకాలు ఉండవు కావున n (∅) = 0
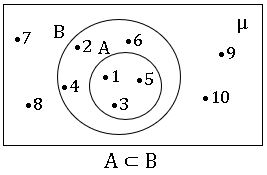
ఉప సమితి: A , B లు రెండు సమితులు, సమితి A లోని ప్రతీ మూలకం సమితి B లో ఉంటే A ని B యొక్క ఉపసమితి అంటారు .దీనిని A ⊂ B అని రాస్తాము.
ఉదా :– A = { 1, 2 , 3, 4 } , B = { 1, 2, 3, 4, 5, 6} ⟹ A ⊂ B
గమనిక :
1) శూన్య సమితి ప్రతి సమితికి ఉప సమితి అవుతుంది.
2) ప్రతి సమితి దానికదే ఉప సమితి అవుతుంది.
విశ్వ సమితి : మన పరిశీలనలో ఉండి, అన్ని ఉప సమితులను కలిగి ఉన్న సమితిని విశ్వ సమితి అంటారు. దీనిని U లేదా 𝜇 చే సూచిస్తాము.
సాధారణంగా విశ్వ సమితిని దీర్ఘచతురస్రం లో ‘ 𝜇’ తో సూచిస్తాము
ఉదా : 1) మన దేశం లో వివిధ రకా లై న ప్రజా సమూహాలను అధ్యయనం చేయాలంటే భారత దేశంలో నివసిస్తున్న ప్రజలందరూ విశ్వ సమితి అవుతారు.
2) ఒక పాఠశాల లోని విద్యార్థులను అధ్యయనం చేయాలంటే , ఆ పాఠశాల లోని విద్యార్థులు అందరూ విశ్వ సమితి అవుతారు.
సమ సమితులు : రెండు సమితులు A మరియు B లు సమానం కావాలంటే A లోని ప్రతీ మూలకం B లో ఉండాలి. అలాగే B లోని ప్రతీ మూలకం A లో ఉండాలి. A మరియు B లు సమ సమితులు అయితే A = B అని రాస్తాము.
ఉదా :- A = {1, 2 ,3, 4 }, B = {3, 2, 1, 4 } ⟹ A = B
గమనిక :
1) A ⊂ B మరియు B ⊂ A అయితే A = B అని రాస్తాము.
2) A ⊂ B , B ⊂ A ⇔ A = B అని కూడ రాయవచ్చు . ఈ ⇔ గుర్తు రెండు వైపులా వర్తిస్తుంది, దీనిని if and only if (‘iff’) అని చదువుతాము.
తుల్య సమితులు : రెండు సమితుల లోని మూలకాల సంఖ్య సమానంగా ఉంటే ఆ సమితులను తుల్య సమితులు అంటారు.
ఉదా :- A = {1, 2 ,3, 4 }, B = {a ,e, I, o }
n (A) = 3 n (B ) = 3
⟹ A ~ B
వెన్ చిత్రాలు :
సమితుల మద్య సంబందాలను సూచించడానికి వెన్ లేదా ఆయిలర్ చిత్రాలను ఉపయోగిస్తాము. ఈ చిత్రాలలో దీర్ఘచతురస్రాలు, సంవృత వక్రాలు సాధారణంగా వృత్తాలు ఉంటాయి.
ఉదాహరణలు:-
→ μ = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }, A = { 1, 3, 5 } B = ( 1,2, 3, 4,5, 6 }
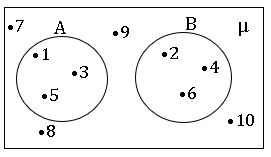
→ μ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 3, 5} B = (2, 4, 6}
సమితులలో ప్రక్రియలు:
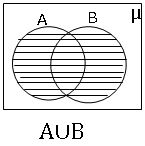
సమితుల సమ్మేళనం :- A సమితిలో గాని B సమితిలో గాని లేదా రెండింటి లో గాని ఉన్న మూలకాలన్నింటినీ కలిగి ఉన్న సమితిని A ,B ల సమ్మేళన సమితి అంటారు. దీనిని A∪ B చే సూచిస్తాము .
A∪ B = {x: x ∈A లేదా x ∈B}
ఉదా :- A = {1, 2, 3}, B = {3, 4, 5}
A ∪ B = {1, 2, 3} ∪ {3, 4, 5}
A ∪ B = {1, 2, 3, 4, 5}
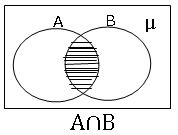
సమితుల ఛేదనం: సమితి A కి మరియు సమితి B కి చెందిన ఉమ్మడి మూలకాలు అలిగి ఉన్న సమితిని A ,B ల ఛేదన సమితి అం టాము.
లాక్షణిక రూపం: A∩ B = {x: x ∈A మరియు x ∈B}
ఉదా :-
A = {1, 2, 3}, B = {3, 4, 5}
A ∩ B = {1, 2, 3} ∩ {3, 4, 5}
A ∩ B = {3}
వి యుక్త సమితులు: ఉమ్మడి మూలకాలు లేని సమితులను వి యుక్త సమితులు అని అంటారు.
- A, B లు వి యుక్త సమితులైన A ∩ B = ∅ అవుతుంది.
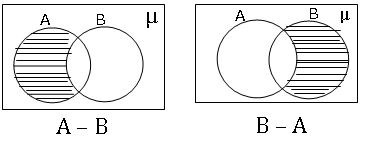
సమితుల భేదం : A , B లు రెండు సమితి లై, A లో ఉంటూ B లో లేని మూలకాల సమితిని A , B సమితుల భేదం అంటారు.
A− B = {x: x ∈A మరియు x ∉ B}, B− A = {x: x ∈ B మరియు x ∉ A }
3.బహుపదులు
బహు పది: చర స్థిర రాశుల తో నిర్మితమైన బీజీయ సమాసాలే బహుదులు. చర రాశులను కొన్ని స్థిర రాశులతో గుణించగా వచ్చు గుణకాలు మరియు వీటిని రునేతర ధన పూర్ణ సంఖ్యల ఘాతాలకు హెచ్చించి వివిధ పరిమాణాలకు రాయబడే బీజీయ సమాసాలను బహుపదులు అంటారు.
ఉదా : 3x + 5 , 4x2 – 3x + 5, x4 మొ ∥నవి బహుపదులు.
బహు పది పరిమాణం : x చర రాశిలో గల బహు పది p (x ) లో x యొక్క గరిష్ఠ ఘాతాంకం p(x) బహుపది యొక్క పరిమాణం అంటారు.
రేఖీయ బహుపది : ఒక బహుపది యొక్క పరిమాణం 1 అయితే ఆ బహు పదిని రేఖీయ బహుపది అంటారు.
సాధారణ రూపం : ax + b
ఉదా : 3x – 5, m + 2, p మొ ∥నవి రేఖీయ బహుపదులు.
వర్గ బహుపది : ఒక బహుపది యొక్క పరిమాణం 2 అయితే ఆ బహు పదిని వర్గ బహుపది అంటారు.
సాధారణ రూపం : ax2 + bx + c
ఆ బహు పదిని రేఖీయ బహుపది అంటారు.
ఉదా : x2 – 3x + 5, 4x2 + 5, మొ ∥నవి వర్గ బహుపదులు.
త్రి పరిమాణ బహుపది : ఒక బహుపది యొక్క పరిమాణం 3 అయితే ఆ బహు పదిని త్రి పరిమాణ బహుపది అంటారు.
సాధారణ రూపం : ax3 + bx2 + cx + d
ఆ బహు పదిని రేఖీయ బహుపది అంటారు.
ఉదా : 3x3 – 5x,+ 4, m3 + 2m2 +4m, మొ ∥నవి త్రి పరిమాణ బహుపదులు.
nవ పరిమాణ బహుపది:
p(x) = a0 xn + a1 xn – 1 + a2 xn – 2 + … + an – 1 x + an ను nవ పరిమాణ బహుపది అం టాము.
బహుపది యొక్క విలువ:
ఒక వాస్తవ సంఖ్య ‘k’ ను, చాల రాశి ‘x’ కు బదులుగా ప్రతిక్షేపిస్తే p(k) అవుతుంది. దీనిని p(x)అనే బహుపది కి k వద్ద వచ్చు విలువ అంటాము.
ఉదా : p(x) = x2 – 2x + 1
x= 1 ⟹ p (1) = (1)2 – 2 (1) + 1
= 1 – 2 + 1
= 0
x= 1 వద్ద p(x) విలువ 0.
x = 2 ⟹ p (2) = (2)2 – 2 (2) + 1
= 4 – 4 + 1
= 1
x=2 వద్ద p(x) విలువ 1.
బహుపది యొక్క శూన్యాలు :
ఒక వాస్తవ సంఖ్య ‘k’ అనేది బహుపది p(x) కు శూన్యం కావాలంటే p(k) = 0 కావాలి .
ఉదా : p(x) = x2 – 2x + 1
x= 1 ⟹ p (1) = (1)2 – 2 (1) + 1
= 1 – 2 + 1
= 0
x= 1 అనేది p(x) కి శూన్య విలువ అవుతుంది.
p(x) = x + 1
x = – 1⟹p (– 1) = – 1 + 1
= 0
x = – 1 అనేది p(x) కి శూన్య విలువ అవుతుంది.
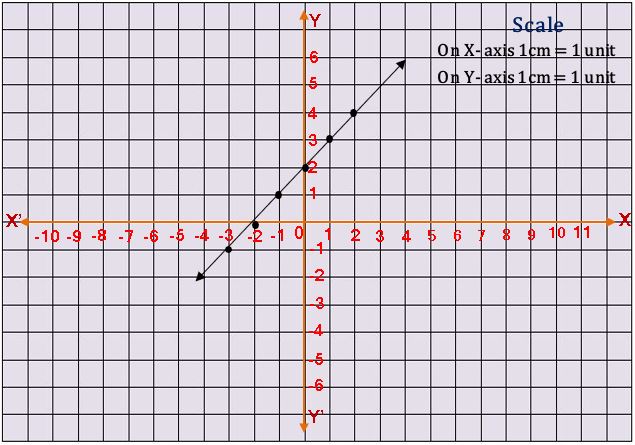
రేఖీయ బహు పది యొక్క రేఖా చిత్రం :.
y = x + 2
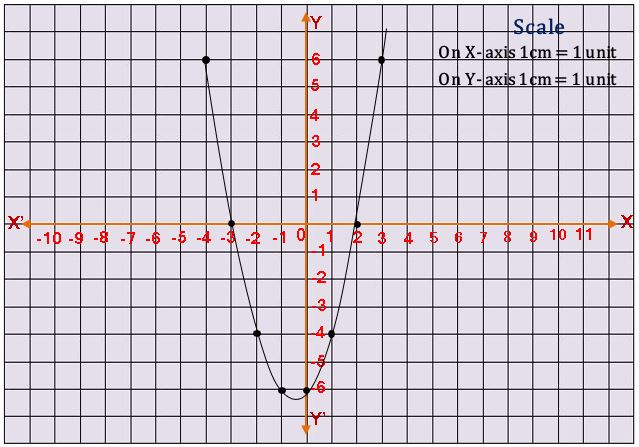
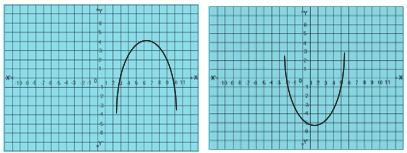
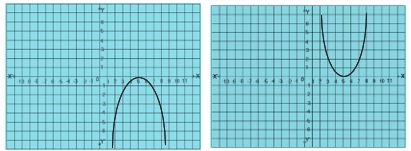
వర్గ బహు పది యొక్క రేఖా చిత్రం :
y = x2 + x – 6
ఈ సందర్భం లో రేఖా చిత్రం x – అక్షం ను రెండు వేర్వేరు బిందువుల వద్ద ఖండించింది. ఆ బిందువుల x నిరూపకాలు వర్గ బహుపది ax2 + bx + c కి శూన్యాలు అవుతాయి. పరావలయం పై వైపునకు గాని, క్రింది వైపునకు గాని విస్తరించబడి ఉంటుంది.
సందర్భం-2 :
ఈ సందర్భం లో రేఖా చిత్రం x – అక్షం ను ఒకే బిందువు
వద్ద ఖండించింది. ఆ బిందువు x నిరూపకం వర్గ బహుపది ax2 + bx + c కి శూన్యం అవుతుంది. పరావలయం పై వైపునకు గాని, క్రింది వైపునకు గాని విస్తరించబడి ఉంటుంది.
ఈ సందర్భం లో రేఖా చిత్రం x – అక్షం ను ఏ బిందువు వద్ద ఖండించదు . వర్గ బహుపది ax2 + bx + c కి శూన్యాలు ఉండవు. పరావలయం పై వైపునకు గాని, క్రింది వైపునకు గాని విస్తరించబడి ఉంటుంది
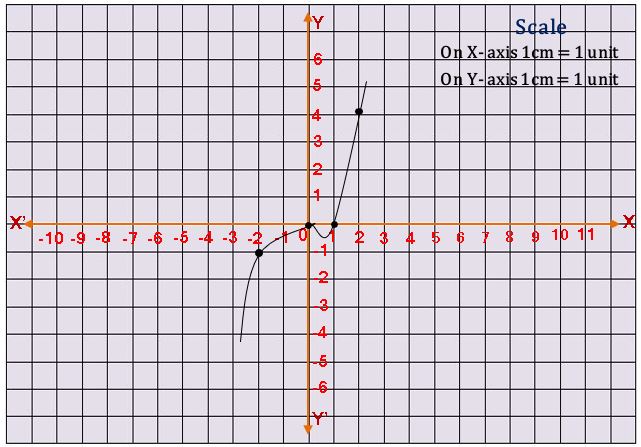
ఘన బహు పది యొక్క రేఖా చిత్రం :
y = x3 – x2
ఒక బహుపది గుణకాలకు, శూన్యాలకు మధ్య సంబంధం:
1.రేఖీయ బహుపది :
p(x)= ax + b
p(x) శూన్యం కావాలంటే ax + b = 0 కావాలి
⟹ax =– b
x = – b/a
2.వర్గ బహుపది :
p(x)= ax2 + bx + c
α, β లు p(x)కు శూన్యాలు అనుకొను ము.
p(x) = k (x – α) (x – β), k ఒక స్థిరాంకం.
= k [x2 – (α + β) x + αβ]
ax2 + bx + c = k x2 – k (α + β) x + k αβ
a = k, b = – k (α + β) మరియు c = k αβ
3.ఘన బహుపది : ఒక బహుపది యొక్క పరిమాణం 1 అయితే ఆ బహు పదిని రేఖీయ బహుపది అంటారు.
p(x)= ax3 + bx2 + cx + d
α, β మరియు γ లు p(x) కు శూన్యాలు అనుకొను ము.
p(x) = k (x – α) (x – β) (x – γ), k ఒక స్థిరాంకం
= k [x2 – (α + β) x + αβ] (x – γ)
ax2 + bx + c = k x2 – K (α + β + γ) x2+k (αβ + β γ +γα) x − k αβγ
a = k, b = – k (α + β + γ), c = k (αβ + β γ +γα) మరియు d= – k αβγ
(α + β + γ) =![]() =
= 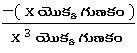 ; αβ + β γ +γα =
; αβ + β γ +γα =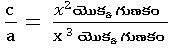 మరియు αβ γ=
మరియు αβ γ=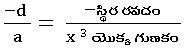
బహుపదుల భాగహార నియమం :
P(x) మరియు g(x) అనేవి రెండు బహుపదులు, g(x)≠0 అయినపుడు రెండు బహుపదులు q(x)మరియు r(x) లను పొందాలంటే P(x) = g(x) × q(x) + r(x)
r(x) = 0 లేదా r(x) పరిమాణం < g(x) యొక్క పరిమాణం
గమనిక :
- q(x) అనేది ఒక రేఖీయ బహుపది అయిన r(x) = r ఓక స్థిరాంకం.
- q(x) యొక్క పరిమాణం 1 అయిన P(x) యొక్క పరిమాణం = 1 + g(x) యొక్క పరిమాణం అగును.
- P(x) ను (x – a) చే భాగిస్తే వచ్చే శేషం P (a) అగును.
- r= 0 అయితే P(x) ను q(x) ఖచ్చితంగా భాగిస్తుంది లేదా q(x) అనేది P(x) యొక్క కారణాంకం అవుతుంది.
4 రెండు చర రాశులలో రేఖీయ సమీకరణాల జత
రేఖీయ సమీకరణం:
a , b ,c లు వాస్తవ సంఖ్యలై a లేదా b సున్నా కానట్టి సమీకరణం a x + b y + c = 0 (a2 + b2 ≠0) ను x , y లలో రేఖీయ సమీకరణం అంటారు.
రేఖీయ సమీకరణాల జత :
ఒకే రకమైన రెండు చర రాశులు గల రెండు రేఖీయ సమీకరణాలను రెండు చర రాశులలో రేఖీయ సమీకరణాల జత అంటారు.
a1x + b1y + c1 = 0 (a12 + b12≠0), a2x + b2 y + c2 = 0 (a22 + b22≠0); a1, a2, b1, b2, c1, c2 లు వాస్తవ సంఖ్యలు.
రెండు చర రాశులలో రేఖీయ సమీకరణాల జతకు సాధనలు :
ఒక తలం లో రెండు సరళ రేఖలు గీసినపుడు . ఈ క్రింది మూడు సందర్భాలలో ఒక్కటి మాత్రమే సాధ్యమగు ను.
- ఆ రెండు సరళ రేఖలు ఒక బిందువు వద్ద ఖండించు కోనును.

- ఆ రెండు సరళ రేఖలు ఖండించుకోవు . అవి సమాంతర రేఖలు.

- ఆ రెండు రేఖలు ఏకీభవించును.

గ్రాఫ్ పద్ధతి ద్వారా రేఖీయ సమీకరణాల జతకు సాధనలు కనుగొనుట:
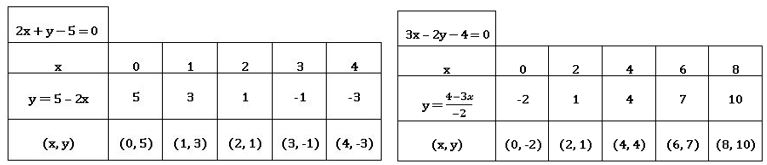
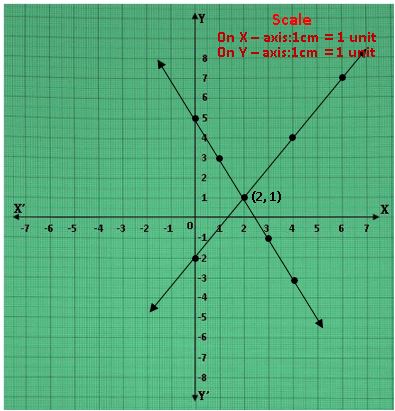
1.2x + y −5 = 0, 3x – 2y − 4 = 0
పై పట్టికలలోని బిందువులను కార్టీ జియన్ తలంలో గుర్తించ గా ఏర్పడిన గ్రాఫ్ ను పరిశీలించగా , రెండు రేఖల ఖండన బిందువు (2, 1).
(2, 1) బిందువు ఇచ్చిన రేఖలకు ఏకైక ఉమ్మడి బిందువు అందువలన రెండు చర రాశులలో రేఖీయ సమీకరణాల జతకు ఒకే ఒక సాధన ఉంటుంది. ఇటువంటి సమీకరణాలను ‘సంగత’ రేఖీయ సమీకరణాల జత అంటారు.
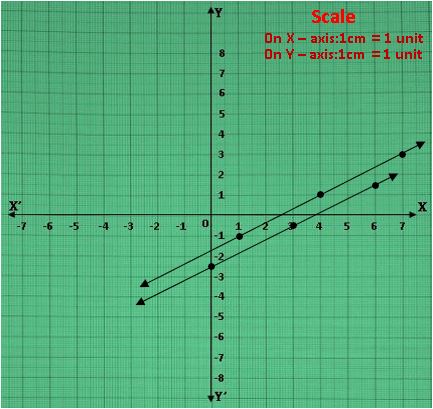
2.2x – 3y = 5; 4x – 6y = 15

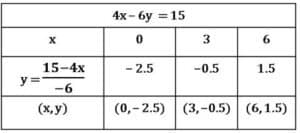
పై పట్టికలలోని బిందువులను కార్టీ జియన్ తలంలో గుర్తించ గా ఏర్పడిన గ్రాఫ్ ను పరిశీలించగా , రెండు రేఖలు ఖండించుకోలేదు.
ఇచ్చిన రేఖలకు ఏకైక ఉమ్మడి బిందువు లేదు. ఇటువంటి సమీకరణాలను ‘అ సంగత’ రేఖీయ సమీకరణాల జత అంటారు.
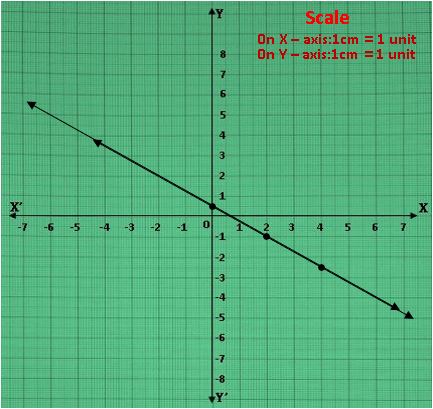
3. 3x + 4y = 2; 6x + 8y = 4
పై పట్టికలలోని బిందువులను కార్టీ జియన్ తలంలో గుర్తించ గా ఏర్పడిన గ్రాఫ్ ను పరిశీలించగా , రెండు రేఖలు ఏకీభవించాయి .
రేఖ పై ఏర్పడిన ప్రతీ బిందువు రెండు సమీకరణాలకు ఉమ్మడి సాధనలు. ఈ సమీకరణాలు తుల్యాలు , వీటికి అనంత సాధనలు ఉంటాయి .
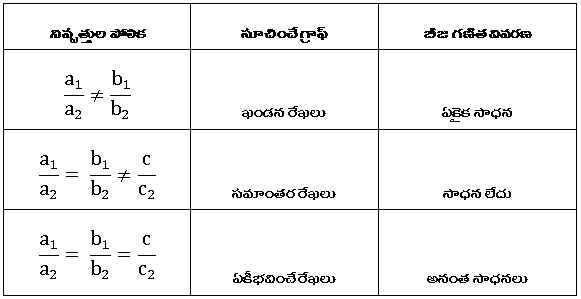
గుణకములు మరియు సమీకరణ వ్యవస్థ స్వభావం మధ్య గల సంబంధం:
రేఖీయ సమీకరణాల జతకు సాధన కనుగొనడానికి బీజ గణిత పద్దతులు:
a1x + b1y + c1 = 0 (a12 + b12≠0), a2x + b2 y + c2 = 0 (a22 + b22≠0) లు సమీకరణాల జత
ప్రతిక్షేపణ పద్ధతి : –
రెండు చర రాశులలో రేఖీయ సమీకరణాల జతకు సాధన కనుగొనుట లో ఒక చర రాశిని, రెండవ చర రాశిని పదాలలో రాసినప్పుడు ఈ పద్ధతి చాలా ఉపయోగం.
ప్రతిక్షేపణ పద్ధతి సోపానాలు :
సోపానం -1 : ఒక సమీకరణం లో ఒక చర రాశిని వేరొక చర రాశి పదాలలో రాయాలి. చర రాశి ‘y’ ని చర రాశి ‘x’ పదముల లొ లేదా చర రాశి ‘x’ ని చర రాశి ‘y’ పదాలలో రాయాలి.
సోపానం -2 : సోపానం 1 లో వచ్చిన చర రాశి y ( లేదా x) విలువను రెండవ సమీకరణం లో ప్రతిక్షేపించాలి.
సోపానం -3 : సోపానం 2 లో వచ్చిన సమీకరణాన్ని సూక్ష్మీకరించి x ( లేదా y) విలువను కనుగొనాలి.
సోపానం -4 : సోపానం 3 లో వచ్చిన x ( లేదా y) విలువను ఇచ్చిన ఎదో ఒక సమీకరణం ప్రతిక్షేపిస్తే y ( లేదా x) వస్తుంది.
సోపానం -5 : వచ్చిన x , y విలువను ఇచ్చిన సమీకరణా లలో ప్రతిక్షేపించి సరి చూడాలి.
ఉదా : x + y = 3 , x – y = 1 లను ప్రతిక్షేపణ పద్ధతిలో సాధించుము.
సాధన:
x + y = 3 ……… (1)
x – y = 1 ……… (2)
(1) నుండి y = 3 – x
y = 3 – x ను సమీకరణం (2) లో ప్రతిక్షేపించగా
x – (3 – x) = 1
x – 3 + x = 1 ⇒2x = 4 ⇒x = 2 వస్తుంది
x = 2 ను సమీకరణం (1) లో ప్రతిక్షేపించగా
2 + y = 3 ⇒y = 3 – 2 ⇒y = 1 వస్తుంది.
x, y విలువలను సమీకరణం (2) లో ప్రతిక్షేపించి సరి చూడాలి
x – y = 1⇒ 2 –1= 1
⇒ 1= 1
∴ ఇచ్చిన సమీకరణాల జతకు సాధన x = 2, y = 1.
చర రాశిని తొలగించు పద్ధతి : –
సమీకరణాలలోని ఒక చర రాశి గుణకాలను సమానం చేయడం ద్వారా ఆ చర రాశిని తొలగిస్తాము. దీని వలన ఒక చర రాశిలో ఒకే సమీకరణం ఏర్పడుతుంది. దీనిని సాధించడం వలన రెండవ చర రాశి వస్తుంది.
చర రాశి తొలగించు పద్ధతి సోపానాలు :
సోపానం -1 : ఇచ్చిన రెండు సమీకరణాలను ax + by = c రూపం లోకి మార్చాలి.
సోపానం -2 : ఆ రెండు సమీకరణాలను సరైన వాస్తవ సంఖ్యలతో గుణించి , ఆ రెండు సమీకరణాలలోని రెండు చర రాశులలో తొలగించ దలచిన ఒక చర రాశి గుణకాన్ని సమానం చేయాలి.
సోపానం -3 : తొలగించ వలసిన చర రాశి గుణకాలు రెండు సమీకరణాలలో ఒకే గుర్తును కలిగివుంటే ఒక సమీకరణం నుండి వేరొక సమీకరణం ను తీసివేస్తే ఒక చర రాశిలో ఒక సమీకరణం వస్తుంది. వాటికి వ్యతిరేక గుర్తులు ఉంటే కూడాలి.
సోపానం -4 : మిగిలిన చర రాశి కొరకు ఆ సమీకరణాన్ని సాధించాలి.
సోపానం -5 : వచ్చిన విలువను ఇచ్చిన రెండు సమీకరణాలలో ఒకదానిలో ప్రతిక్షేపించి , ముందు తొలగించిన చర రాశి విలువను కనుక్కోవాలి .
ఉదా : 2x – y = 5 , 3x + 2 y = 11 లను చర రాశి తొలగించు పద్ధతిలో సాధించుము.
సాధన :
2x – y = 5 ……. (1)
3x + 2 y = 11……. (2)
⇒ x = 3
x = 3 విలువను సమీకరణం (1) లో ప్రతిక్షేపించగా
2x – y = 5 ⇒ 2(3) – y = 5 ⇒ 6 – y = 5
6 -5 = y ⇒ y = 1.
కావలసిన సాధన x = 3, y = 1.
5. వర్గ సమీకరణం
వర్గ సమీకరణం: a, b, c లు వాస్తవ సంఖ్య లై a ≠0 అయిన ax2 + bx + c = 0 ను ‘x’ లో వర్గ సమీకరణం అంటాము. p(x) ఒక ద్వి పరిమాణ బహుపది అవుతూ p(x) = 0 రూపం లో వున్న వాటన్నిటి ని వర్గ సమీకరణాలు అంటారు.
ax2 + bx + c = 0, a ≠0 నకు aα2 + bα+ c = 0 అయిన α ను వర్గ సమీకరణం యొక్క మూలం అంటారు.
ax2 + bx + c వర్గ బహుపది యొక్క శూన్య విలువలు, ax2 + bx + c = 0 వర్గ సమీకరణ మూలాలు ఒక్కటే.
వర్గ సమీకరణ సాధన పద్దతులు:
1.కారణాంక పద్ధతి:
ax2 + bx + c = 0, a ≠0 ఇచ్చిన వర్గ సమీకరణం
కారణాంక పద్ధతి న వర్గ సమీకరణ సాధనకు సోపానాలు :
సోపానం -1: మధ్య పదమును రెండు పదాలుగా విడగొట్టాలి.
సోపానం -2 : మధ్య పదమును రెండు పదాలుగా విడగొట్టుటకు p + q = b మరియు p ×q= a × c.అయ్యే విధంగాp, q లను కనుగొనాలి.
సోపానం -3 : p, q లను కనుగొనుటకు a × c విలువ యొక్క కారణాంకాల జాబితాను తయారు చేయాలి.
సోపానం -4 : p + q = b మరియు p ×q= a × c లను తృప్తి పరిచే జతను ఎన్నుకొని ఇచ్చిన సమీకరణాన్ని కారణాంకాల లబ్దంగా రాసి సమీకరణ మూలాలను కనుక్కోవాలి.
ఉదా : కారణాంక పద్ధతిన 2x2 + 5x + 3 = 0 యొక్క మూలాలను కనుగొనుము
సాధన : ఇచ్చిన సమీకరణం 2x2 + 5x + 3 = 0
p + q = 5; p ×q= 6
6 యొక్క కారణాంకాల జాబితా: (1, 6), (-1, -6), (2, 3), (-2, -3)
(2, 3) అనే జత p + q = 5; p ×q= 6 లను తృప్తి పరుస్తుంది
⇒ 2x2 + 5x + 3 = 0 ను 2x2 +(2 + 3)x + 3 = 0 గా రాయవచ్చు
⇒2x2 +2x + 3x + 3 = 0 ⇒ 2x ( x + 1) + 3 (x +1) = 0
⇒ (x + 1) (2x + 3) = 0 ⇒ (x+1) = 0 లేదా (2x + 3)= 0
∴ x = -1, -3/2 లు సాధనలు.
2.వర్గమును పూర్తి చేయుట ద్వారా వర్గ సమీకరణ సాధన:
ax2 + bx + c = 0, a ≠0 ఇచ్చిన వర్గ సమీకరణం
వర్గమును పూర్తి చేయుట ద్వారా వర్గ సమీకరణ సాధనకు సోపానాలు :
సోపానం -1: ఇచ్చిన సమీకరణం లోని స్థిర పదమును కుడి వైపుకు తీసుకువెళ్లి ఇరువైపుల a చే భాగించాలి.
సోపానం -2 : ఎడమ భాగమును సంపూర్ణ వర్గముగా మార్చుటకు సమీకరణముకు ఇరువైపుల ![]() ను కూడాలి.
ను కూడాలి.
సోపానం -3 : ఎడమ భాగాన్ని వర్గం చేసి కుడి భాగాన్ని సూక్ష్మీకరించాలి.
సోపానం -4 : సోపానం-3 ను సాధిస్తే ఇచ్చిన సమీకరణానికి మూలాలు వస్తాయి.
ఉదా : వర్గమును పూర్తి చేయుట ద్వారా 2x2 + 5x + 3 = 0 యొక్క మూలాలను కనుగొనుము
సాధన : ఇచ్చిన సమీకరణం 2x2 + 5x + 3 = 0
3.సూత్రం ద్వారా వర్గ సమీకరణ సాధన:
ax2 + bx + c = 0, a ≠0 వర్గ సమీకరణం కు మూలాలు
ఉదా : సూత్రం ద్వారా 2x2 + 5x + 3 = 0 యొక్క మూలాలను కనుగొనుము
సాధన : ఇచ్చిన సమీకరణం 2x2 + 5x + 3 = 0
మూలాల స్వభావం:
విచక్షిణి: b2 – 4ac అనేది ax2 + bx + c = 0, a ≠0 వర్గ సమీకరణం కు విచక్షిణి.
- b2 – 4ac >0 అయిన మూలాలు విభిన్న వాస్తవ సంఖ్యలు.
- b2 – 4ac =0 అయిన మూలాలు సమాన వాస్తవ సంఖ్యలు.
- b2 – 4ac < 0 అయిన మూలాలు లేవు.
6 . శ్రేఢులు
శ్రేఢి: ఒక ప్రత్యేక సూత్రం ను అనుసరించి ప్రతీ పదము దాని పూర్వ పదముతో సంబంధం కలుగునట్లు రాయగల సంఖ్యల వరుసను శ్రేఢి అంటారు.
ఉదా: 1, 3,5,7,9,…
2,4,6,8,10,…
శ్రేఢులు రకాలు:
శ్రేఢులు మూడు రకాలు : అవి:
- అంక శ్రేఢి (Arithmetic progression)
- గుణ శ్రేఢి(Geometric progression)
- హరాత్మక శ్రేఢి(Hormonic progression) [10 వ తరగతి సిలబస్ లో లేదు]
1.అంక శ్రేఢి (Arithmetic progression): –
ఒక సంఖ్యల జాబితాలో మొదటి పదం తప్ప మిగిలిన అన్ని పదాలు వాటి ముందున్న పదానికి స్థిర సంఖ్యను కలపడం వల్ల వచ్చే ఆ జాబితాను అంక శ్రేఢి అంటాము.
స్థిర పదమును ‘సామాన్య భేదం’ లేదా ‘పధాంతరం’ అంటారు. ఇది ఋణాత్మకం లేదా ధనాత్మకం లేదా సున్నా కావచ్చు.
అంక శ్రేఢి యొక్క సాధారణ రూపం:
a, a + d, a + 2d, ……., a + (n – 1) d ను అంక శ్రేఢి యొక్క సాధారణ రూపం అంటారు.
∗మొదటి పదం = a
∗సామాన్య భేదం (d) = a2 – a1= a3 – a2=….= an – an-1
∗n వ పదం a n =a + (n – 1) d
∗n పదాల మొత్తం
∗ a , b, c అంక శ్రేఢి లో ఉంటే b ని a, c మధ్య అంక మధ్యమం అంటారు. 2b = a + c.
2.గుణ శ్రేఢి(Geometric progression):-
ఒక సంఖ్యల జాబితాలో మొదటి పదం తప్ప మిగిలిన అన్ని పదాలు వాటి ముందున్న పదానికి స్థిర సంఖ్యను గుణించడం వల్ల వచ్చే ఆ జాబితాను గుణ శ్రేఢి అంటాము.
స్థిర పదమును ‘సామాన్య నిష్పత్తి ’ అంటారు. ఇది ఋణాత్మకం లేదా ధనాత్మకం కావచ్చు.
గుణ శ్రేఢి యొక్క సాధారణ రూపం:
a, ar, a r2, ……., arn-1 ను గుణ శ్రేఢి యొక్క సాధారణ రూపం అంటారు.
∗మొదటి పదం = a
∗n వ పదం an =arn-1
∗n పదాల మొత్తం =
∗ a , b, c గుణ శ్రేఢి లో ఉంటే b ని a, c మధ్య గుణ మధ్యమం అంటారు. b 2 = a c.
3.హరాత్మక శ్రేఢి(Hormonic progression):-
ఒక శ్రేఢి లోని పదముల విలోమములు అంక శ్రేఢి లో ఉంటే ఆ శ్రేఢి ని హరాత్మక శ్రేఢి.
హరాత్మక శ్రేఢి యొక్క సాధారణ రూపం:
![]() ను హరాత్మక శ్రేఢి యొక్క సాధారణ రూపం అంటారు.
ను హరాత్మక శ్రేఢి యొక్క సాధారణ రూపం అంటారు.
7 . నిరూపక రేఖా గణితం
రేఖా గణిత, బీజ గణిత అనుసంధానం తో ఏర్పడినదే నిరూపక రేఖా గణితం. దీనినే వైశ్లేషిక రేఖా గణితం లేదా కార్టీసియన్ రేఖా గణితం అంటారు.
నిరూపక రేఖా గణితానికి మూల పురుషుడు రెనే డెకార్టె .
రెండు బిందువుల మధ్య దూరం:
- X – అక్షం పై ఉన్న బిందువులు A (x1, 0), B (x2, 0) అయిన వాటి మధ్య దూరం

- Y – అక్షం పై ఉన్న బిందువులు A (0, y1), B (0, y2) అయిన వాటి మధ్య దూరం

- X – అక్షానికి సమాంతరంగా ఉండే రేఖపై ఉన్న బిందువులు A (x1, y1), B (x2, y1) అయిన వాటి మధ్య దూరం

- Y – అక్షానికి సమాంతరంగా ఉండే రేఖ పై ఉన్న బిందువులు A (x1, y1), B (x1, y2) అయిన వాటి మధ్య దూరం

- నిరూపక తలంలో ఉండే రేఖపై ఉన్న బిందువులు A (x1, y1), B (x2, y2) అయిన వాటి మధ్య దూరం

విభజన సూత్రం :
బిందువులు A (x1, y1) మరియు B (x2, y2) లచే ఏర్పడు రేఖను అంతరంగా m1 : m2 నిష్పత్తి లో విభజించే బిందువు P (x, y) యొక్క నిరూపకాలు ![]()
బిందువులు A (x1, y1) మరియు B (x2, y2) లచే ఏర్పడు రేఖను బాహ్యంగా m1 : m2 నిష్పత్తి లో విభజించే బిందువు P (x, y) యొక్క నిరూపకాలు ![]()
మధ్య బిందువు సూత్రం :
రెండు బిందువులు A (x1, y1) మరియు B (x2, y2) లచే ఏర్పడు రేఖా యొక్క మధ్య బిందువు 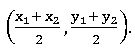
త్రిభుజం యొక్క గురుత్వ కేంద్రం: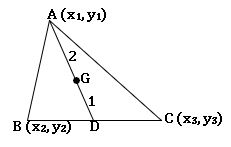
ఒక త్రిభుజం లోని మధ్యగత రేఖల మిళిత బిందువును గురుత్వ కేంద్రం అంటారు. దీనిని G చే సూచిస్తాము.
గురుత్వ కేంద్రం యొక్క నిరూపకాలు![]()
గురుత్వ కేంద్రం మధ్యగత రేఖను 2 : 1 నిష్పత్తి లో విభజిస్తుంది.
రేఖ యొక్క త్రిథాకరణ బిందువులు:
ఒక రేఖాఖండమును మూడు సమాన భాగాలుగా విభజించు బిందువులను ‘త్రిథాకరణ బిందువులు’ అంటారు.
AB రేఖా ఖండము యొక్క త్రిథాకరణ బిందువులు P మరియు Q అయిన AP = PQ = QB
AB రేఖా ఖండమును P బిందువు అంతరంగ 1: 2 నిష్పత్తి లో విభజిస్తుంది.
AB రేఖా ఖండమును Q బిందువు అంతరంగ 2: 1 నిష్పత్తి లో విభజిస్తుంది.
త్రిభుజ వైశాల్యం:
A (x1, y1), B (x2, y2) మరియు C (x3, y3) శీర్షాలు గల త్రిభుజం యొక్క వైశాల్యం
హెరాన్ సూత్రం:
a, b, c లు భుజాల పొడవులు గల త్రిభుజ వైశాల్యం ![]()
బిందువుల సరేఖీయత :
ఒకే తలంలోని కొన్ని బిందువులు ఒకే రేఖా పై ఉంటే ఆ బిందువులనే సరేఖీయ బిందువులు అంటారు.
మూడు బిందువులతో ఏర్పడు త్రిభుజ వైశాల్యం సున్నా అయితే ఆ బిందువులు సరేఖీయాలు.
సరళ రేఖ వాలు:
ఏదేని ఒక సరళ రేఖ X – అక్షం తో ధనాత్మక దిశలో θ కోణం చేస్తే tan θ ను ఆ రేఖ యొక్క వాలు అంటారు. వాలును m చే సూచిస్తాము.
m = tan𝛉
రెండు బిందువులు A (x1, y1) మరియు B (x2, y2) లచే ఏర్పడు రేఖా యొక్క వాలు![]()
8 . సరూప త్రిభుజాలు
సరూప పటములు: ఒకే ఆకారం గల పటములన్నిటినీ సరూప పటములు అంటారు.
క్రమ బహుభుజి: ఒక బహుభుజి లో భుజాలన్నీ మరియు కోణాలన్నీ సమానంగా వుంటే దానిని క్రమ బహుభుజి అంటారు.
సరూప బహుభుజులు: రెండు బహుభుజులు సరూపములు కావాలంటే
- వాటి అను రూప కోణములు సమానం కావాలి.
- వాటి అను రూప భుజములు అనుపాతంలో ( ఒకే నిష్పత్తిలో)ఉండాలి.
సరూప త్రిభుజములు: రెండు త్రిభుజాలు సరూపములు కావాలంటే
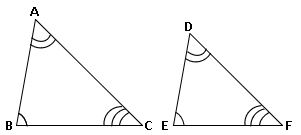
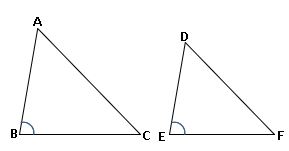
రెండు త్రిభుజాలు ∆ABC, ∆DEF లు సరూపాలు అయితే
గుర్తులలో ∆ABC~ ∆DEF అని వ్రాస్తాము. (~ సరూపపు గుర్తు)
గమనిక :
K > 1 అయిన పెద్దవి చేయబడిన పటాలు
K = 1అయిన సర్వ సమాన పటాలు
K < 1 అయిన చిన్నవి చేయబడిన పటాలు ఏర్పడుతాయి.
ప్రాథమిక అనుపాత సిద్ధాంతం (థేల్స్ సిద్ధాతం) :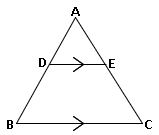
ఒక త్రిభుజం లోని ఒక భుజానికి సమాంతరంగా గీసిన రేఖ మిగిలిన రెండు భుజాలను వేరు వేరు బిందువులలో ఖండించిన , ఆ మిగిలిన రెండు భుజాలు ఒకే నిష్పత్తిలో విభజించబడతాయి.
∆ABC లో DE ∥ BC అయిన![]()
ప్రాథమిక అనుపాత సిద్ధాంత విపర్యయం :
ఒక త్రిభుజం ఏవైన రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు సరళరేఖ , మూడవ భుజానికి సమాంతరంగా ఉంటుంది.
త్రిభుజాల సరూపత నియమాలు:
రెండు త్రిభుజాలలో అనురూప కోణాలు సమానంగా ఉంటె , వాటి అనురూప భుజాల నిష్పత్తులు సమానంగా ఉంటాయి. ఆ రెండు త్రిభుజాలు సరూప త్రిభుజాలు అవుతాయి.
∆ABC, ∆DEF లలో ∠A=∠D, ∠B =∠E , ∠C =∠F అయిన ![]()
∆ABC ~ ∆DEF
రెండు త్రిభుజాలలో, ఒక త్రిభుజంలోని భుజాలు వేరొక త్రిభుజంలోని భుజాలకు అనుపాతంలో వున్నా ఆ రెండు త్రిభుజాలలోని అనురూప కోణాలు సమానం . ఆ రెండు త్రిభుజాలు సరూపాలు.
∆ABC, ∆DEF లలో ![]() అయిన ∠A=∠D, ∠B =∠E , ∠C =∠F
అయిన ∠A=∠D, ∠B =∠E , ∠C =∠F
∆ABC ~ ∆DEF
ఒక త్రిభుజంలోని ఒక కోణం , వేరొక త్రిభ్జంలోని ఒక కొనమునకు సమానమై, ఆ కోణాలు కలిగివున్న భుజాలు అనుపాతంలో వుంటే ఆ త్రిభుజాలు సరూపాలు .
∆ABC, ∆DEF లలో ∠B =∠E మరియు ![]() అయిన ∆ABC ~ ∆DEF
అయిన ∆ABC ~ ∆DEF
సరూప త్రిభుజాల వైశాల్యాలు:
రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల నిష్పత్తి వర్గమునకు సమానం.
∆ABC, ∆PQR లలో ∆ABC ~ ∆PQR అయిన
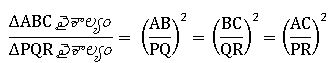
పైథాగరస్ సిద్ధాంతం (బౌధాయన సిద్ధాంతం) :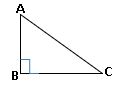
ఒక లంబకోణ త్రిభుజంలో కర్ణము మీది వర్గము, మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానం.
∆ABC లో ∠B = 900 అయిన AC2 = AB2 + BC2
పైథాగరస్ సిద్ధాంత విపర్యయం :
ఒక త్రిభుజంలో ఒక భుజం మీది వర్గము, మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానమైన, మొదటి భుజానికి ఎదురుగా వుండే కోణం లంబకోణం మరియు ఆ త్రిభుజం లంబకోణ త్రిభుజం అవుతుంది.
∆ABC లో AC2 = AB2 + BC2 అయిన ∠B = 900
9 . వృత్తాలకు స్పర్శ రేఖలు మరియు చేధన రేఖలు
ఒక తలంలో ఓకే స్థిర బిందువు నుండి , స్థిర దూరంలో ఉన్నట్టి బిందువుల సమితిని వృత్తం అంటారు.
స్థిర బిందువును వృత్త కేంద్రమని, స్థిర దూరంను వృత్త వ్యాసార్థం అని అంటారు.
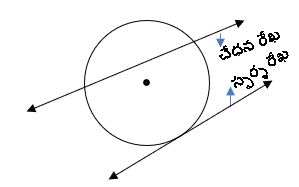
ఒక వృత్తాన్ని రెండు బిందువుల వద్ద ఖండించే సరళ రేఖను ఖండిత రేఖ లేదా చేధన రేఖ అంటారు.
స్పర్శ రేఖ:
ఒక సరళ రేఖ, వృత్తమును ఒకే ఒక బిందువు వద్ద తాకుతూ వెళితే ఆ సరళ రేఖను స్పర్శ రేఖ అంటారు.
స్పర్శ రేఖా అను పదం ‘టాన్ గ్రీ‘ అనే లాటిన్ పదం నుండి వచ్చింది. దీని అర్థం స్పర్శించడం.
∗ఒక వృత్తానికి అనంతమైన స్పర్శ రేఖలు గీయగలము.
గమనిక :
వృత్త అంతరం లో గల ఏ బిందువు నుండైన వృత్తానికి స్పర్శ రేఖా గీయలేము.
- వృత్తం పై గల ఏ బిందువు నుండైన వృత్తానికి ఒకే ఒక స్పర్శ రేఖా గీయగలము
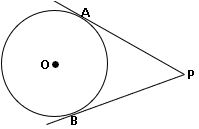
- వృత్త బాహ్యంలో గల ఏ బిందువు నుండైన వృత్తానికి ఖచ్చితంగా రెండు స్పర్శ రేఖలు గీయగలము
∗ ఒక వృత్తం పై గల ఏదైనా బిందువు గుండా గీయబడిన స్పర్శ రేఖ, ఆ స్పర్శ బిందువు వద్ద వ్యాసార్థానికి లంబంగా ఉంటుంది.
∗ ఒక తలంలో వృత్తం పై వ్యాసార్థం యొక్క చివరి బిందువు గుండా గీయబడిన రేఖ దానికి లంబంగా వున్నచో ఆ రేఖ వృత్తానికి స్పర్శ రేఖ అగును.
∗ వృత్తానికి బాహ్య బిందువు నుండి గీయబడిన స్పర్శ రేఖల మధ్య ఏర్పడే కోణ సమద్విఖండన రేఖ పై ఆ వృత్తం యొక్క కేంద్రం ఉంటుంది.
∗ వృత్తానికి బాహ్య బిందువు గుండా గీయబడిన స్పర్శ రేఖల పొడవులు సమానం.
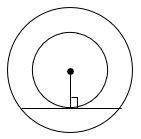
∗ రెండు ఏక కేంద్ర వృత్తాలలో బాహ్య వృత్తం యొక్క జ్యా , అంతర వృత్తం యొక్క స్పర్శ బిందువు వద్ద సమద్విఖండన అగును.
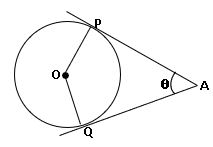
∗ O కేంద్రముగా గల వృత్తానికి బాహ్య బిందువు A నుండి గీయబడిన స్పర్శ రేఖలు AP మరియు AQ అయిన
∠PAQ = 2 ∠OPQ =2 ∠OQP
∗ ఒక వృత్తం ABCD చతుర్భుజాన్ని P ,Q ,R, S ల వద్ద తాకిన AB + CD = BC + DA
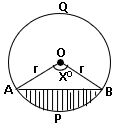
సెక్టార్ వైశాల్యం = 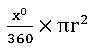
APB వృత్త ఖండ వైశాల్యం = OAPB సెక్టార్ వైశాల్యం − ∆AOB వైశాల్యం
AQB వృత్త ఖండ వైశాల్యం = వృత్త వైశాల్యం − APB వృత్త ఖండ వైశాల్యం
10 . క్షేత్రమితి
క్షేత్రమితి: జ్యామితి పటాల వైశాల్యాలను, ఘనపరిమాణాలను గణించే గణిత విభాగమును క్షేత్రమితి అంటారు.
దీర్ఘఘనం :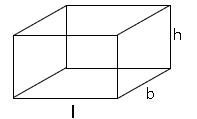
దీర్ఘఘనం నకు 3 ముఖ తలాలు, 12 అంచులు,8 శీర్షాలు ఉంటాయి.
పొడవు = l; వెడల్పు = b మరియు ఎత్తు = h అయిన
ఉపరితల వైశాల్యం = 2h (l + b )చ. ప్రమాణాలు.
సంపూర్ణ తల వైశాల్యం = 2(lb + b h + hl )చ. ప్రమాణాలు.
ఘనపరిమాణం = lbh ఘ .ప్రమాణాలు
సమఘనం :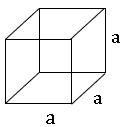
సమఘనం నకు 3 ముఖ తలాలు, 12 అంచులు,8 శీర్షాలు ఉంటాయి.
సమఘనపు భుజం = a అయిన
ఉపరితల వైశాల్యం = 4a2 చ. ప్రమాణాలు.
సంపూర్ణ తల వైశాల్యం = 6a2చ. ప్రమాణాలు.
ఘనపరిమాణం = a3 ఘ .ప్రమాణాలు
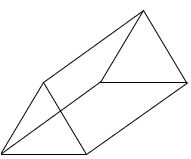
ఉపరితల వైశాల్యం = (భుపరిది× ఎత్తు) చ. ప్రమాణాలు.
సంపూర్ణ తల వైశాల్యం = (వక్రతల వైశాల్యం + 2× చివరి కారణాల వైశాల్యం)చ. ప్రమాణాలు.
ఘనపరిమాణం = (భూ వైశాల్యం × ఎత్తు) ఘ .ప్రమాణాలు.
క్రమ వృత్తాకార స్థూపం: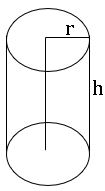
స్థూప భూ వ్యాసార్థం = r మరియు స్థూపం ఎత్తు = h అయిన
ఉపరితల వైశాల్యం = 2πrh చ. ప్రమాణాలు.
సంపూర్ణ తల వైశాల్యం =2πr(r + h) చ. ప్రమాణాలు.
ఘనపరిమాణం = πr2h ఘ .ప్రమాణాలు. 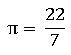
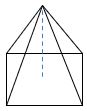
క్రమ వృత్తాకార శంకువు :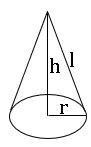
భూ వ్యాసార్థం = r; స్థూపం ఎత్తు = h మరియు ఏటవాలు ఎత్తు l అయిన
ఉపరితల వైశాల్యం = πrl చ. ప్రమాణాలు.
సంపూర్ణ తల వైశాల్యం =πr(r + l) చ. ప్రమాణాలు.
ఘనపరిమాణం = ![]() πr2h ఘ .ప్రమాణాలు .
πr2h ఘ .ప్రమాణాలు . 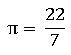
ఉపరితల వైశాల్యం = 2πrh చ. ప్రమాణాలు.
సంపూర్ణ తల వైశాల్యం =2πr(r + h) చ. ప్రమాణాలు.
ఘనపరిమాణం = πr2h ఘ .ప్రమాణాలు. 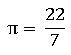
ఉపరితల వైశాల్యం = 4πr2 చ. ప్రమాణాలు.
సంపూర్ణ తల వైశాల్యం = 4πr2 చ. ప్రమాణాలు.
ఉపరితల వైశాల్యం = 2πr2 చ. ప్రమాణాలు.
సంపూర్ణ తల వైశాల్యం = 3πr2 చ. ప్రమాణాలు.
11 . త్రికోణమితి
త్రిభుజం లోని మూడు కోణాల కొలతను త్రికోణమితి అంటారు. దీనిని ఆంగ్లంలో Trigonometry అని అంటారు, ఈ పదం గ్రీక్ భాష లోని trigonon , metron అనే పదాలనుండి పుట్టింది. trigonon అంటే త్రిభుజం metron అంటే మాపనం అని అర్థం.
కోణం: ఒకే ఉమ్మడి అంత్య బిందువు కలిగిన రెండు కిరణాల సమ్మేళనాన్ని కోణం అంటారు.
సవ్య పరిభ్రమణం: గడియారంలో ముళ్ళు ఏ దిశలో తిరుగు నో , అదే దిశలో అంతిమ భుజం తిరుగుతున్నపుడు ఆ భ్రమణాన్ని సవ్య పరిభ్రమణం అంటారు. ఈ దశలో చేసిన కోణాన్ని ధనాత్మక పరిమాణంగా తీసుకుంటారు.
అప సవ్య పరిభ్రమణం: గడియారంలో ముళ్ళు తిరిగే దిశకు వ్యతిరేక దిశలో అంతిమ భుజం తిరుగుతున్నపుడు ఆ భ్రమణాన్ని అప సవ్య పరిభ్రమణం అంటారు. ఈ దశలో చేసిన కోణాన్ని ఋనాత్మక పరిమాణంగా తీసుకుంటారు.
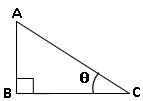
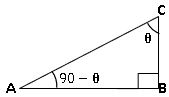
AB = θ యొక్క ఎదుటి భుజం
BC = θ యొక్క ఆసన్న భుజం
AC = కర్ణం
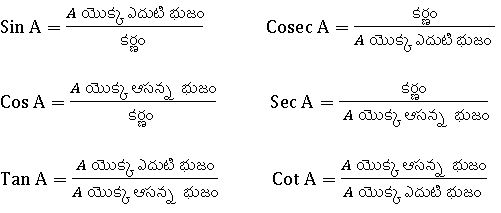
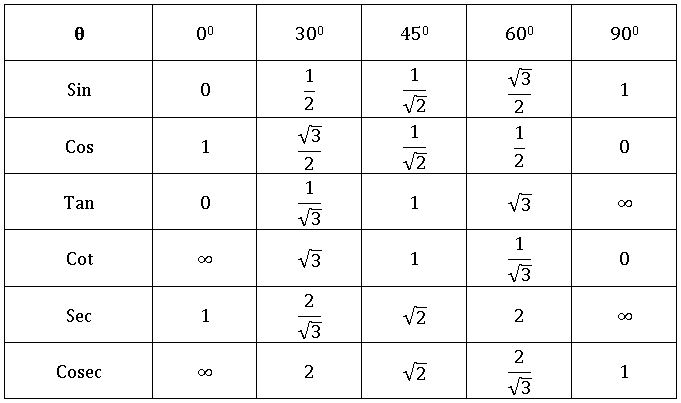
త్రికోణమితీయ నిష్పత్తులు:
కోణాలు – త్రికోణమితీయ నిష్పత్తులు:
పూరక కోణాలు మరియు త్రికోణమితీయ నిష్పత్తుల మధ్య సంబంధం :
పూరక కోణాలు:- రెండు కోణాల మొత్తం 900 అయిన ఆ కోణాలను పూరక కోణాలు అంటారు.
∠B = 900 అయిన ∠C = 𝛉 అనుకొనుము అపుడు ∠A = 900 − 𝛉 అగును.
పై వాటి నుండి
sin (90 – θ) = cos θ; cos (90 – θ) = sin θ
tan (90 – θ) = cot θ; cot (90 – θ) = tan θ
sec (90 – θ) = cosec θ; cosec (90 – θ) = sec θ
త్రికోణమితీయ సర్వ సమీకరణాలు:
1) sin2A + cos2A = 1
sin2A = 1 – sin2A; cos2A = 1 – sin2A
2) sec2 – tan2A = 1
sec2A = 1 + tan2A; tan2A = sec2A – 1
3) cosec2A – cot2A = 1
cosec2A = 1 + cot2A; cot2A = cosec2A – 1
12 . త్రికోణమితి అనువర్తనాలు
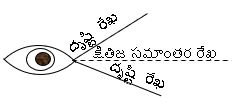
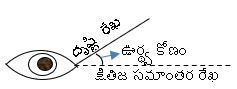
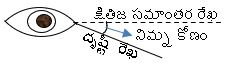
దృష్టి రేఖ : ఒక వస్తువు పైనున్న ఒక బిందువు నుండి పరిశీలకుని కాంతిని కలిపే రేఖను దృష్టి రేఖ అంటారు.
క్షితిజ సమాంతర రేఖ : పరిశీలకుని కంటి నుండి భూమికి సమాంతరంగా ఉండే విధంగా ఊహించే రేఖను క్షితిజ సమాంతర రేఖ అంటారు.
ఊర్థ్వ కోణం :దృష్టి రేఖ, క్షితిజ సమాంతర రేఖకు పైన ఉంటే క్షితిజ సమాంతర రేఖ తో దృష్టి రేఖ చేయు కోణంను ఊర్థ్వ కోణం అంటారు.
నిమ్న కోణం :దృష్టి రేఖ, క్షితిజ సమాంతర రేఖకు క్రింద ఉంటే క్షితిజ సమాంతర రేఖ తో దృష్టి రేఖ చేయు కోణంను నిమ్న కోణం అంటారు.
గమనిక :
ఎత్తులు మరియు దూరాలకు సంబంధించిన సమస్యలు సాధించడానికి కింది విషయాలను దృష్టిలో పెట్టుకోవాలి.
- గణిత పరంగా సౌలభ్యం కొరకు టవర్లు, చెట్లు, భవనాలు, ఓడలు, పర్వతాలు మొ∥ వాటిని రేఖీయంగానే పరిగణనలోకి తీసుకోవాలి.
- ఊర్థ్వ కోణం లేదా నిమ్న కోణాన్ని క్షితిజ సమాంతర రేఖ ఆధారంగా తీసుకోవాలి.
- సమస్యలో పరిశీలుస్తున్న వ్యక్తి ఎత్తు కుంటే , అతని ఎత్తుని ఉపేక్షించి సమస్యను సాధించాలి.
13. సంభావ్యత
యాదృచ్చిక ప్రయోగం: ఒక ప్రయోగంలో ఏ ఫలితం వస్తుందో ముందే చెప్పలేనిదై, ఆ ప్రయోగ ఫలితాల జాబితా ముందే తెలిసి ఉండి, ఒకే విధమైన పరిస్థితులలో ఎన్ని సార్లు అయినా చేయడానికి వీలుంటే, ఆ ప్రయోగాన్ని యాదృచ్చిక ప్రయోగం అంటారు.
ఘటన : ఒక యాదృచ్చిక ప్రయోగంనకు చెందిన ప్రతీ ఫలితాన్ని లఘు ఘటన లేదా ప్రాథమిక ఘటన అంటారు.
సంభావ్యత – ప్రాయోగిక వివరణ :
ఒక ఘటన (E ) యొక్క ప్రాయోగిక సంభావ్యత P (E ) ను లెక్కించుటకు సూత్రం
సంభావ్యత – సైద్దాంతిక వివరణ :
T అనే ఘటన యొక్క సైద్దాంతిక సంభావ్యత P (T) ను లెక్కించుటకు సూత్రం
పరస్పర వివృత లేదా విసర్జిత ఘటనలు:
ఒక ప్రయోగంలోని రెండు లేక అంతకన్నా ఎక్కువ ఘటనలలో ఒక ఘటన యొక్క సంభవము మిగిలిన అన్ని ఘటనల సంభవమును నిరోధిస్తే, ఆ ఘటనలను పరస్పర వివృత లేదా విసర్జిత ఘటనలు అంటారు.
పూర్ణ ఘటనలు: ఒక ప్రయోగంలోని అన్ని ఘటనల సమ్మేళనం ప్రతిరూప ఆవరణం అయిన , వాటిని పూర్ణ ఘటనలంటారు.
సమసంభవ ఘటనలు: ఒక ప్రయోగం లోని రెండు లేక అంతకన్నా ఎక్కువ ఘటనలు సంభవించడానికి సమాన అవకాశములు ఉంటే వాటిని సమసంభవ ఘటనలు అంటారు.
పూరక ఘటనలు – సంభావ్యత :
‘E కానిది’ అను ఘటనను ![]() చే చూపుతాము. దీనిని E యొక్క ‘పూరక ఘటన’ అంటాము.
చే చూపుతాము. దీనిని E యొక్క ‘పూరక ఘటన’ అంటాము.
అసాధ్య లేదా అసంభవ ఘటన : ఒక ప్రయోగంలో ఒక ఘటన ఎప్పుడూ సాధ్యపడక పోతే దానిని అసాధ్య ఘటన అంటారు.
ఖచ్చిత ఘటన: ఒక ప్రయోగం లోని ఒక ఘటన యొక్క సంభవము ఖచ్చితం మరియు సంభావ్యత 1 అయిన దానిని ఖచ్చిత లేదా దృఢ ఘటన అంటారు.
గమనిక :సంభావ్యత నిర్వచనం లోని లవము ఎల్లప్పుడు హారము కనా తక్కువ లేదా సమానము కావచ్చు. 0 ≤ P(E) ≤ 1.
పేక ముక్కలు – సంభావ్యత :
పేక ముక్కల కట్టలో 52 కార్డులు ఉంటాయి. వాటిలో ఒక్కొక్కటి 13( A, 1,2,3,4,5,6,7,8,9,10, J, Q, K గుర్తించబడిన) కార్డులు గల 4 విభాగాలుగా ఉంటాయి. ఆ విభాగాల గుర్తులు నలుపు స్పేడులు ( ![]() ) నలుపు కళావర్లు(
) నలుపు కళావర్లు( ![]() ) ఎరుపు హృదయం గుర్తులు (
) ఎరుపు హృదయం గుర్తులు (![]() ) మరియు ఎరుపు డైమండ్లు (
) మరియు ఎరుపు డైమండ్లు ( ![]() ).
).
A ను ఏస్ అని, J ను జాకీ అని, Q ను రాణి అని మరియు K ను రాజు అని అంటారు.
14.సాంఖ్యక శాస్త్రం
సాంఖ్యక శాస్త్రాన్ని ఆంగ్లంలో ‘స్టాటిస్టిక్స్’ అని అంటారు. ఈ పదం ‘స్టాటస్’ అనే లాటిన్ పదం నుండి, ‘స్టాటిస్టా’ అనే ఇటాలియన్ పదం నుండి లేదా ‘స్టాటిస్టిక్స్’ అనే గ్రీకు పదం నుండి ఆవిర్భవించింది. వీటి అర్థం ‘రాజ్యం’.
సాంఖ్యక శాస్త్ర పితామహుడు సర్ రోనాల్డ్ ఫిషర్ .
సాంఖ్యక శాస్త్రం :దత్తాంశ సేకరణ, వర్గీకరణ, వ్యాఖ్యానాలతో కూడిన గణిత శాస్త్ర విభాగాన్ని ‘సాంఖ్యక శాస్త్రం’ అంటారు.
కేంద్రీయ స్థాన విలువలు :
కేంద్రీయ స్ధాన విలువలు మూడు రకాలు అవి: (i) అంకగణిత సగటు (ii) మధ్య గతం (iii) బాహులకం
అంకగణితం :
అవర్గీకృత దత్తాంశం యొక్క అంకగణిత సగటు:
• x1, x2, …. xn రాశుల యొక్క అంకగణిత సగటు ![]()
• x1, x2, …. xn రాశుల యొక్క పౌనఃపున్యాలు వరుసగా f1, f2, …. fn సార్లు పునరావృతం అయిన అంకగణిత సగటు
వర్గీకృత దత్తాంశం యొక్క అంక గణిత సగటును కనుగొనే పద్దతులు :
ప్రత్యక్ష పద్ధతి : 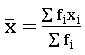 ; xi అనేది i వ తరగతి మధ్య విలువ;fi అనగా i వ తరగతి పౌనఃపున్యం .
; xi అనేది i వ తరగతి మధ్య విలువ;fi అనగా i వ తరగతి పౌనఃపున్యం .
విచలన పద్ధతి లేదా ఊహించిన సగటు పద్ధతి : ![]() ; di = xi – a మరియు a అనేది ఊహించిన సగటు.
; di = xi – a మరియు a అనేది ఊహించిన సగటు.
సోపాన విచలన పద్ధతి: 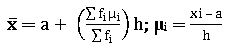 , h అనేది తరగతి అంతరం .
, h అనేది తరగతి అంతరం .
మధ్యగతం
దత్తాంశం లోని రాశుల యొక్క మధ్య విలువలను మధ్యగతం ఇస్తుంది.
అవర్గీకృత దత్తాంశం యొక్క మధ్యగతం:
- ముందుగా దత్తాంశంలో ఇచ్చిన రాశులను ఆరోహణ క్రమంలో అమర్చాలి.
- ఒకవేళ రాశుల సంఖ్య ‘n’ బేసి సంఖ్య అయిన మధ్యగతం =
 వ రాశి
వ రాశి - ‘n’ సరి సంఖ్య అయిన మధ్యగతం =

అవర్గీకృత దత్తాంశం యొక్క మధ్యగతం:
l = మధ్యగత తరగతి దిగువ హద్దు
n = దత్తాంశంలోని రాశుల సంఖ్య
f = మధ్యగత తరగతి యొక్క పౌనఃపున్యం
h = మధ్యగత తరగతి అంతరం
బాహులకం
•ఇవ్వబడిన రాశులలో ఎక్కువ సార్లు పునరావృతం అయ్యే రాశిని ‘బాహులకం’ అంటారు.
l = బాహులక తరగతి దిగువ హద్దు
f0 = బాహులక తరగతికి ముందున్న తరగతి యొక్క పౌనఃపున్యం
f1 = బాహులక తరగతి యొక్క పౌనఃపున్యం
h = బాహులక తరగతి అంతరం
•అంకగణిత సగటు, మధ్యగతము మరియు బాహులకము ల మధ్య అనుభావిక సంబంధం :
బాహులకం = 3(మధ్యగతం ) – 2(అంకగణిత సగటు) .
Visit my YouTube channel: Click on the Logo