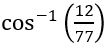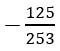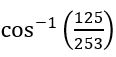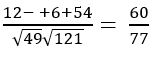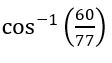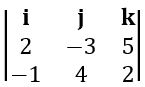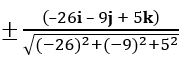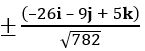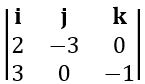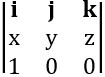Product of Vectors (Qns.& Ans) V.S.A.Q.’S

Product of Vectors (Qns.& Ans) V.S.A.Q.’S

Product of Vectors (Qns.& Ans) V.S.A.Q.’S; These solutions were designed by the ‘Basics in Maths‘ team. These notes to do help intermediate First-year Maths students.

Inter Maths – 1A two marks questions and solutions are very useful in IPE examinations.

Product Of Vectors

Question 1

If a = 6i +2 j +3 k, b = 2i – 9 j+ 6k, then find the angle between the vectors a and b

Sol:

Given vectors are a = 6i +2 j +3 k, b = 2i – 9 j+ 6k

 If θ is the angle between the vectors 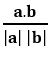a and b, then cos θ = 

 a .b = (6i +2 j +3 k). (2i – 9 j+ 6k) = 6(2) + 2 (– 9) + 3(6)

          = 12 – 18 + 18 = 12

              = 7

              = 11

  ⟹ cos θ =

 θ =

Question 2

If a = i +2 j –3 k, b = 3i – j+ 2k, then show that a + b and a – b are perpendicular to each other.

Sol:

Given vectors are a = i +2 j –3 k, b = 3i – j+ 2k

a + b = (i +2 j –3 k) + (3i – j+ 2k) = 4i + j – k

a – b = (i +2 j –3 k) – (3i – j+ 2k) = –2i +3 j – 5k

(a + b). (a – b) = (4i + j – k). (–2i +3 j – 5k)

                            = – 8 + 3 + 5

                           = 0

∴ a + b and a – b is perpendicular to each other.

Question 3

If a and b be non-zero, non-collinear vectors. If , then find the angle between a and b

Sol:

Given

 Squaring on both sides

 (a + b) (a + b) = (a – b) (a – b)

  a² + 2 a. b + b² = a² – 2 a.b + b²

 ⟹ 4 a.b = 0

  a.b = 0

∴ the angle between a and b  is 90⁰

Question 4

If = 11, = 23 and  = 30, then find the angle between the vectors a and b and also find

Sol:

Given = 11,   = 23 and = 30

        = 30

 = 900

 = 900

(11)² – 2 ×11×23 cos θ + (23)² = 900

121 – 506 cos θ + 529   = 900

 650 – 506 cos θ = 900

cos θ =  ⟹ θ =

                = (11)² + 2 ×11×23 cos θ + (23)²

                = 121 + 2 ×11×23 ×  + 529

               = 400

 = 20

Question 5

If a = i – j – k and b = 2i – 3j + k, then find the projection vector of b on a and its magnitude.

Sol:

Given vectors are a = i – j – k and b = 2i – 3j + k

 a.b = (i – j – k). (2i – 3j + k) = 2 + 3 – 1 = 4

   =

 The projection vector of b on a =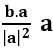

                  =  (i – j – k)

  The magnitude of the projection vector =  =

Question 6

If the vectors λ i – 3j + 5k and 2λ i – λ j – k are perpendicular to each other, then find λ

Sol:

let a = λ i – 3j + 5k, b = 2λ i – λ j – k

Given, that a and b are perpendicular to each other

⟹ a.b = 0

(λ i – 3j + 5k). (2λ i – λ j – k) = 0

2 λ² + 3 λ – 5 = 0

2 λ² + 5 λ – 2 λ – 5 = 0

λ (2 λ + 5) – 1 (2 λ + 5) = 0

(2 λ + 5) ((λ – 1) = 0

λ = 1 or λ = -5/2

Question 7

Find the Cartesian equation of the plane passing through the point (– 2, 1, 3) and perpendicular to the vector 3i + j + 5k

Sol:

let P (x, y, z) be any point on the plane

 ⟹ OP = xi + yj + zk

 OA = – 2i +j +3k

AP = OP – OA = (xi + yj + zk) – (– 2i +j +3k)

 AP = (x + 2) i + (y – 1) j + (z – 3) k

 AP is perpendicular to the vector 3i + j + 5k

 ⟹ 3 (x + 2) + (y – 1) + 5(z – 3) = 0

  ⟹ 3x + 6 + y – 1 + 5z – 15 = 0

 ∴   3x + y + 5z – 10 = 0 is the required Cartesian equation of the plane

Question 8

Find the angle between the planes 2x – 3y – 6z = 5 and 6x + 2y – 9z = 4

Sol:

Given plane equations are: 2x – 3y – 6z = 5,6x + 2y – 9z = 4

 Vector equations of the above planes are: r. (2i – 3j – 6k) = 5 and r. (6i + 2j – 9k) = 4

 ⟹ n₁ = 2i – 3j – 6k and n₂ = 6i + 2j – 9k

 If θ is the angle between the planes r. n₁ = d₁ and r. n₂ = d₂, then

 Cos θ =

  ⟹ Cos θ =

 ⟹ θ =

Question 9

a = 2i – j + k, b = i – 3j – 5k. Find the vector c such that a, b, and c form the sides of a triangle.

Sol:

Given a = 2i – j + k, b = i – 3j – 5k

 If a, b, and c form the sides of a triangle, then a + b + c = 0

 ⟹ a + b = – c

⟹ c = – (a + b)

       = – [(2i – j + k) +( i – 3j – 5k)]

      = – (3i –4 j –4k)

     ∴ c = – 3i +4 j + 4k     

Question 10

Find the equation of the plane through the point (3, –2, 1) and perpendicular to the vector (4, 7, –4).

Sol:

 Let a = 3i – 2j + k and n = 4i + 7j – 4k

 The equation of the plane passing through point A(a) and perpendicular to the vector n is (r – a). n = 0

 ⟹ [r – (3i – 2j + k)]. (4i + 7j – 4k) = 0

 ⟹ r. (4i + 7j – 4k)– [(3i – 2j + k). (4i + 7j – 4k)] = 0

r. (4i + 7j – 4k)– (12 – 14 – 4) = 0

r. (4i + 7j – 4k)– 6 = 0

r. (4i + 7j – 4k) = 6

Question 11

Find the unit vector parallel to the XOY-plane and perpendicular to the vector 4i – 3j + k

Sol:

The vector which is parallel to the XOY-plane is of the form xi + yj

The vector which is parallel to the XOY-plane and perpendicular to 4i – 3j + k

 is 3i + 4j

 its magnitude =     = 5

∴ The unit vector parallel to the XOY-plane and perpendicular to the vector 4i – 3j + k =

Question 12

If a + b + c = 0, = 3,  = 5 and    = 7, then find the angle between a and b

Sol:

Given, a + b + c = 0,  = 3,  = 5 and    = 7

 a + b = – c

 (a + b)² =

 3² + 5² + 2  cos θ = 7²

  9 + 25 + 2.3.5 cos θ = 49

 34 + 30cos θ = 49

 30cos θ = 49 – 34

 30cos θ = 15

cos θ = 15/30 = 1/2

∴ θ = π/3

Question 13

If a = 2i – 3j + 5k, b = – i + 4j + 2k, then find a × b and unit vector perpendicular to both a and b

Sol:

 Given, a = 2i – 3j + 5k, b = – i + 4j + 2k             

 a × b =

         = i (–6 – 20) – j (4 + 5) + k (8 – 3)

         = –26i – 9j + 5k

The unit vector perpendicular to both a and b    =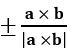  

  =

=

Question 14

If a = i + j + 2k and b = 3i + 5j – k are two sides of a triangle, then find its area.

Sol:

Given, a = i + 2j + 3k and b = 3i + 5j – k

If a, b are two sides of a triangle, then area of the triangle =

a × b =

         = i (–2 – 15) – j (–1 – 9) + k (5 – 6)

         = –17i + 10 j – k

 =

Area of triangle = =

                              =

Question 15

Find the area of the parallelogram for which the vectors a = 2i – 3j and b = 3i – k are adjacent sides.

Sol:

Given, a = 2i – 3j and b = 3i – k are adjacent sides of a parallelogram

The area of the parallelogram whose vectors a , b are adjacent sides =  

  a × b=

              = i (3 – 0) – j (–2 – 0) + k (0 + 9)

             =3 i +2 j +9 k

=

                =

∴ The area of the parallelogram =

Question 16

Let a, b be two non-collinear unit vectors. If α = a – (a . b) b and β = a × b, then show that

Sol:

=

          =

              = 1 – cos² θ

             = sin² θ

 =

        = 1 + cos² θ – 2cos² θ

       = 1– cos² θ

       = sin² θ

∴

Question 17

For any vector a, show that     

Sol:

Let a = xi + yj + zk

       a × i =

                = i ( 0 – 0) – j (0 – z) + k (0 – y)

           = – yk + zj

   = y² + z²        

Similarly,  = x² + z²      and      = y² + x²        

+ +  = y² + z² + x² + z² + y² + x²        

                                                        = 2(x² + y² +z²)

                                                        =2

Question 18

If = 2,  = 3 and (p, q) = , then find

Sol:

Given = 2,  = 3 and (p, q) =

  =  sin (p, q)

                = 2 × 3 sin

                = 2 × 3×1/2

               = 3

 = 3² = 9

Question 19

If 4i + j + pk is parallel to the vector i + 2j + 3k, then find p.

Sol:

Given 4i +  j + pk is parallel to the vector i + 2j + 3k

   =  =

 = 4

⇒ p = 12

Question 20

Compute a× (b + c) + b× (c + a) + c× (a + b)

Sol:

a× (b + c) + b× (c + a) + c× (a + b)

= a× b + a× c + b× c + b× a + c × a + c × b

= a× b + a× c + b× c –a × b – a × c – b ×c

= 0

Question 21

Compute 2j× (3i – 4k) + (i + 2j) × k

Sol:

2j× (3i – 4k) + (i + 2j) × k

= 6(j × i) – 8(j × k) + (i × k) + 2(j × k)

 = – 6k – 8i – j + 2i

 = – 6i –j –6 j

Visit my Youtube Channel: Click on Below Logo