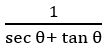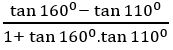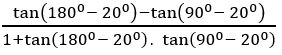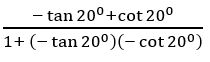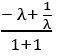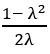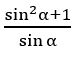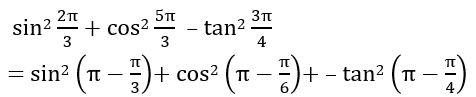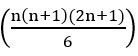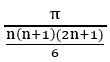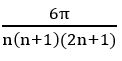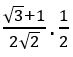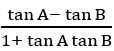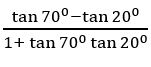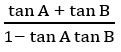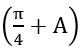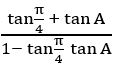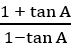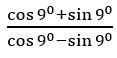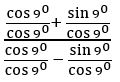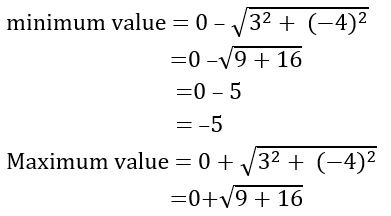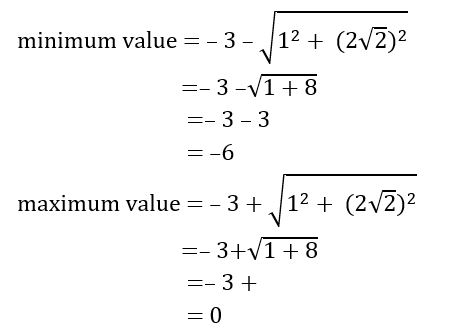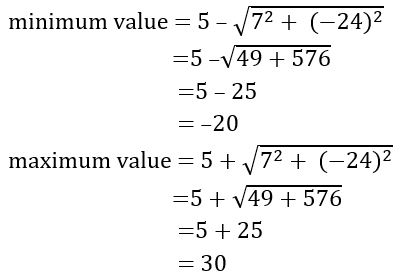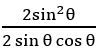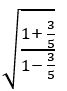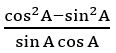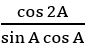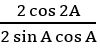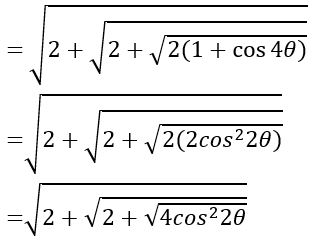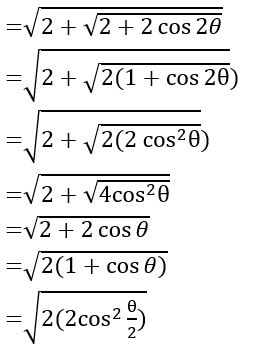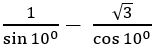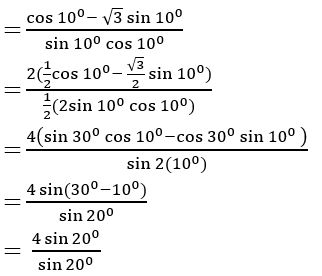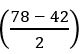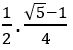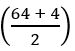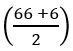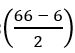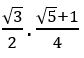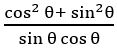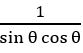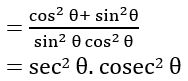Trigonometric Ratios(Qns.& Ans) V.S.A.Q.’S

Trigonometric Ratios(Qns.& Ans) V.S.A.Q.’S designed by the ‘Basics in Maths‘ team.These notes to do help intermediate First-year Maths students.

Inter Maths – 1A two marks questions and solutions are very useful in I.P.E examinations.

Trigonometric Ratios Up to Transformations

 Question 1

Find the value of sin²(π/10) + sin²(4π/10) + sin²(6π/10) + sin²(9π/10)

Sol:

 sin²(π/10) + sin²(4π/10) + sin²(6π/10) + sin²(9π/10)

= sin²(π/10) + sin²(π/2 – π/10) + sin²(π/2+ π/10) + sin²(π – π/10)

= sin²(π/10) + cos²(π/10) + cos²(π/10) + sin²(π/10)

= 1 + 1 = 2

 Question 2

If sin θ = 4/5 and θ not in the first quadrant, find the value of cos θ

Sol:

Given sin θ = 4/5 and θ not in the first quadrant

⇒ θ in the second quadrant

⇒ cos θ < 0

    cos²θ = 1 – sin² θ

              =1 – (4/5)²

             = 1 – 16/25

∴cos θ   = – 3/5 (∵cos θ < 0)

 Question 3

If 3sin θ + 4 cos θ = 5, then find the value of 4 sin θ – 3cos θ

Sol:

Given, 3sin θ + 4 cos θ = 5

let 4 sin θ – 3cos θ = x

  (3sin θ + 4 cos θ )² + (4 sin θ – 3cos θ)² = 5² + x²

 9 sin² θ + 16 cos² θ + 12 sin θ cos θ + 16 sin² θ + 9 cos² θ – 12sin θ cis θ = 25 + x²

25 sin² θ + 25 cos² θ = 25 + x²

25 = 25 + x²

⇒ x² = 0

 x = 0

∴ 4 sin θ – 3cos θ = 0

 Question 4

If sec θ + tan θ =, find the value of sin θ and determine the quadrant in which θ lies

Sol:

Given, sec θ + tan θ =  ———— (1)

 We know that sec² θ – tan² θ = 1

⇒ (sec θ + tan θ) (sec θ – tan θ) = 1

 sec θ – tan θ =

⇒ sec θ – tan θ = ———— (2)

 (1) + (2)

⇒ (sec θ + tan θ) + (sec θ – tan θ) =

2sec θ =

 sec θ =

(1) – (2)

⇒ (sec θ + tan θ) – (sec θ – tan θ) =

2 tan θ =  ⇒ tan θ =

Now sin θ = tan θ ÷ sec θ =

     Sin θ =

Since sec θ positive and tan θ is negative θ lies in the 4^th quadrant.

 Question 5

Prove that cot (π/16). cot (2π/16). cot (3π/16).… cot (7π/16) = 1

Sol:

cot (π/16). cot (2π/16). cot (3π/16).… cot (7π/16)

= cot (π/16). cot (2π/16). cot (3π/16). cot (4π/16). cot (5π/16) cot (6π/16) cot (7π/16)

= cot (π/16). cot (2π/16). cot (3π/16). cot (π/4). cot (π/2 – 3π/16) cot (π/2 – 2π/16) cot (π/2 – π/16)

= cot (π/16). cot (2π/16). cot (3π/16). cot (π/4). tan (3π/16) tan (2π/16) tan (π/16)

= [cot (π/16). tan (π/16)] [cot (2π/16). tan (2π/16)] [cot (3π/16). tan (3π/16]. cot (π/4)

= 1.1.1.1

 =1

 Question 6

If cos θ + sin θ = cos θ, then prove that cos θ – sin θ =  sin θ

Sol:

Given, cos θ + sin θ = cos θ

Sin θ =  cos θ – cos θ

           = (  – 1) cos θ

(  + 1) sin θ = (  + 1) (  – 1) cos θ

 sin θ + sin θ = cos θ

∴ cos θ – sin θ =  sin θ

 Question 7

Find the value of 2(sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ)

Sol:

2(sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ)

= 2[(sin² θ)³ + (cos² θ)³] – 3[(sin² θ)² + (cos²)²

= 2[(sin² θ + cos² θ)³ – 3 sin² θ cos² θ (sin² θ + cos² θ)] – 3[(sin² θ + cos² θ)² – 2 sin² θ cos² θ]

= 2[1 – 3 sin² θ cos² θ] – 3 [1 – 2 sin² θ cos² θ]

= 2 – 6 sin² θ cos² θ – 3 + 6 sin² θ cos² θ

= – 1

 Question 8

If tan 20⁰ = λ, then show that    

Sol:

Given tan 20⁰ = λ

 =

                               =

                              =

                              =

 Question 9

If sin α + cosec α = 2, find the value of sinⁿ α + cosecⁿ α, n∈ Z

Sol:

Given sin α + cosec α = 2

 ⇒ sin α + 1/ sin α = 2

 ⇒  = 2

      sin² α + 1= 2 sin α

       sin² α – 2 sin α + 1= 0

  (sin α – 1 )² = 0

⇒ sin α – 1 = 0

sin α = 1 ⇒ cosec α = 1

 sinⁿ α + cosecⁿ α = (1)ⁿ + (1)ⁿ =1 + 1 =2

∴ sinⁿ α + cosecⁿ α = 2

 Question 10

Evaluate sin² + cos²   – tan²  

Sol:

 Question 11

Find the value of sin 330⁰. cos 120⁰ + cos 210⁰. Sin 300⁰

Sol:

 sin 330⁰. cos 120⁰ + cos 210⁰. Sin 300⁰

=sin (360⁰ – 30⁰). cos (180⁰ – 60⁰) + cos (180⁰ + 30⁰). sin (360⁰ – 60⁰)

= (– sin 30⁰). (– cos 60⁰) + (– cos30⁰). (– sin60⁰)

= sin 30⁰.  cos 60⁰ + cos30⁰.  Sin60⁰

= sin (60⁰ + 30⁰) = sin 90⁰

=1

 Question 12

Prove that cos⁴ α + 2 cos² α = (1 – sin⁴ α)

Sol:

cos⁴ α + 2 cos² α

= cos⁴ α + 2 cos² α (1 – cos² α)

= (cos² α)² + 2 (1 – sin² α) (sin² α)

= (1 – sin² α)² + 2 sin² α – 2sin⁴ α

= 1 + sin⁴ α – 2 sin² α + 2 sin² α – 2sin⁴ α

= 1 – sin⁴ α

 Question 13

Eliminate θ from x = a cos³ θ and y = b sin³ θ

Sol:

Given x = a cos³ θ and y = b sin³ θ

 cos³ θ = x/a and sin³ θ = y/b

 cos θ = (x/a)^1/3 and sin θ = (y/b)^1/3

we know that sin² θ + cos² θ = 1

 ⇒ [(y/b)^1/3]² + [(x/a)^1/3]² = 1

   (x/a)^2/3 + (y/b)^2/3 = 1

 Question 14

Find the period of the following functions

Sol:

(i) f(x) = tan 5x

we know that period of tan kx =

⇒ period of tan 5x =

(ii) f(x) =

we know that period of =

period of =

                                      =

(iii) f(x) = 2 sin + 2 cos

period of sin  =  = 8

period of cos  =  = 6

period of given function is = LCM (8, 6) = 24

(iv) f(x) = tan (x + 4x + 9x +…. + n²x)

f(x) = tan (x + 4x + 9x +…. + n²x)

       = tan (1 + 4 + 9 + … + n²) x

= tanx

we know that period of tan kx =

Period of tan  =

                        =

 Question 15

Prove that sin²(52 ½)⁰ – sin² (22 ½)⁰ =

Sol:

We know that sin² A – sin²B = sin (A +B) sin (A – B)

 ⇒ sin²(52 ½)⁰ – sin² (22 ½)⁰

= sin (52 ½+ 22 ½) sin (52 ½ – 22 ½)

 = sin 75⁰ sin 30⁰

 =       

∴ sin²(52 ½)⁰ – sin² (22 ½)⁰ =

 Question 16

Prove that tan 70⁰ – tan20⁰ = 2 tan 50⁰

Sol:

50⁰ = 70⁰ – 20⁰

Tan 50⁰ = tan (70⁰ – 20⁰)

We know that tan (A –B) =

  ⇒ Tan 50⁰ =

 ⇒ tan 70⁰ – tan 20⁰ = tan 50⁰ (1 + tan70⁰ tan 20⁰)

     tan 70⁰ – tan 20⁰ = tan 50⁰ [1 + tan70⁰ cot (90⁰ – 20⁰)]

     tan 70⁰ – tan 20⁰ = tan 50⁰ [1 + tan70⁰ cot 70⁰]

     tan 70⁰ – tan 20⁰ = tan 50⁰ [1 + 1]

∴ tan 70⁰ – tan20⁰ = 2 tan 50⁰

 Question 17 

If sin α = , sin β =  and α, β are acute, show that α + β =

Sol:

Given sin α =                                               sin β =

 tan α = 1/3                                                          tan β = ½

tan (α + β) =

  tan (α + β) = 1

∴ α + β =

 Question 18

Find tan in terms of tan A

Sol:

 tan  =

                        =

 Question 19

Prove that = cot 36⁰

Sol:

  =

(on dividing numerator and denominator by cos 9⁰)

      =

   = tan (45⁰ + 9⁰)

    = tan 54⁰

 = tan (90⁰ – 36⁰)

 = cot 36⁰

 ∴  = cot 36⁰      

 Question 20

Show that cos 42⁰ + cos 78⁰ + cos 162⁰ = 0

Sol:

cos 42⁰ + cos 78⁰ + cos 162⁰

= cos (60⁰ – 18⁰) + cos (60⁰ + 18⁰) + cos (180⁰ – 18⁰)

=cos 60⁰ cos18⁰ + sin 60⁰ sin 18⁰ + cos 60⁰ cos 18⁰ – sin 60⁰ sin 18⁰ – cos 18⁰

= 2 cos 60⁰ cos 18⁰ – cos 18⁰

= 2 (1/2) cos 18⁰ – cos 18⁰

 = cos 18⁰ – cos 18⁰

= 0

 Question 21

Express sin θ + cos θ as a single of an angle

Sol:

sin θ + cos θ = 2(  sin θ + cos θ)

                                = 2(cos 30⁰ sin θ + sin 30⁰ cos θ)

                                = 2 sin (θ + 30⁰)

 Question 22

Find the maximum and minimum value of the following functions

(i) 3 sin x –4 cos x

a= 3, b = –4 and c = 0

                                     = 5

∴ minimum value = –5 and maximum value = 5

(ii) cos (x + ) + 2  sin (x + ) – 3

a= 1, b = 2  and c = – 3

 ∴ minimum value = –6 and maximum value = 0

 Question 23

Find the range of the function f(x) = 7 cos x – 24sin x + 5

Sol:

Given f(x) = 7 cos x – 24sin x + 5

a= 7, b = –24 and c = 5

∴ Range = [–20, 30]    

 Question 24

Prove that sin²α + cos² (α + β) + 2 sin α sin β cos (α + β) is independent of α

Sol:

sin²α + cos² (α + β) + 2 sin α sin β cos (α + β)

= sin²α + cos (α + β) [ cos (α + β) +2 sin α sin β]

= sin²α + cos (α + β) [ cos α cos β – sin α sin β +2 sin α sin β]

=sin²α + cos (α + β) [ cos α cos β + sin α sin β]

=sin²α + cos (α + β) cos (α –β)

= sin² α + cos² α – sin² β

=1 – sin² β

= cos² β

 Question 25

Simplify

Sol:

   =

                 =

                 = tan θ

Question 26

For what values of x in the first quadrant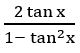 is positive?

Sol:

 > 0 ⟹ tan 2x > 0

⟹ 0 < 2x < π/2 (∵ x is in first quadrant)

⟹ 0 < x < π/4

Question 27

If cos θ = and π < θ < 3π/2, find the value of tan θ/2.

Sol:

cos θ =

π < θ < 3π/2 ⟹ π/2 < θ/2 < 3π/4

tan θ/2 < 0

tan θ/2 =

               =–  (tan θ/2 < 0)

              =–

           = – 2

Question 28

If A is not an integral multiple of π/2, prove that cot A – tan A = 2 cot 2A.

Sol:

cot A – tan A =

                         =

                          =

                          =

                           =

                           = 2 cot 2A

Question 29

Evaluate 6 sin 20⁰ – 8sin³ 20⁰

Sol:

6 sin 20⁰ – 8sin³ 20⁰ = 2 (3 sin 20⁰ – 4sin³ 20⁰)

                                       = 2 sin 3(20⁰)

                              = 2 sin 60⁰

                              = 2 

                              =

Question 30

Express cos⁶ A + sin⁶ A in terms of sin 2A.

Sol:

cos⁶ A + sin⁶ A

= (sin² A)³ + (cos² A)³

= (sin² A + cos² A)³ – 3 sin² A cos² A (sin² A + cos² A)

= 1 – 3 sin² A cos² A

=1 – ¾ (4 sin² A cos² A)

 = 1 – ¾ sin²2 A

Question 31

If 0 < θ < π/8, show that 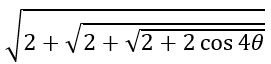 = 2 cos (θ/2)

Sol:

 =2 cos (θ/2)

Question 32

Find the extreme values of cos 2x + cos²x

Sol:

cos 2x + cos²x = 2cos² x– 1 + cos² x

                              =3cos² x – 1

We know that – 1 ≤ cos x ≤ 1

 ⟹ 0 ≤ cos² x ≤ 1

      3×0 ≤ 3×cos² x ≤ 3×1

      0– 1 ≤3 cos² x – 1≤ 3– 1

   – 1≤3 cos² x – 1≤ 2

     Minimum value = – 1

     Maximum value = 2

Question 33

Prove that = 4

Sol:

= 4

Question 34

Prove that sin 78⁰ + cos 132⁰ =

Sol:

 sin 78⁰ + cos 132⁰ = sin 78⁰ + cos (90⁰ + 42⁰)

                                      = sin 78⁰ – sin 42⁰

                                      = 2 cos  sin

                                     = 2 cos 60⁰ sin 18⁰

                                      = 2

                                      =

Question 35

Find the value of sin 34⁰ + cos 64⁰ – cos4⁰

Sol:

sin 34⁰ + cos 64⁰ – cos4⁰

= sin 34⁰ –2 sin  sin

= sin 34⁰ – 2sin 34⁰ sin 30⁰

= sin 34⁰ – 2 sin 34⁰ (1/2)

=sin 34⁰ – sin 34⁰

=0

Question 36

Prove that 4(cos 66⁰ + sin 84⁰) =

Sol:

4(cos 66⁰ + sin 84⁰)  

=4(cos 66⁰ + sin (90⁰ – 6⁰)  

=4(cos 66⁰ + cos (6⁰)  

= 4[ 2 cos  cos ]

=4[ 2 cos  cos ]

=8 cos 36⁰ cos 30⁰

= 8

=

Question 35

Prove that (tan θ + cot θ)² = sec² θ + cosec² θ = sec² θ. cosec² θ

Sol:

tan θ + cot θ =   

                         =

                         =

                         = sec θ. cosec θ

(tan θ + cot θ)²   = sec² θ. cosec² θ

sec² θ + cosec² θ =

                              = sec² θ. cosec² θ

Visit my Youtube Channel: Click on Below Logo