3D Coordinates (Q’s & Ans) || V.S.A.Q’S||

These solutions were designed by the ‘Basics in Maths‘ team. These notes to do help intermediate First-year Maths students.

Inter Maths – 1B two mark questions and solutions are very useful in IPE examinations.

3D Coordinates

1. Show that the points A (– 4, 9, 6), B (– 1, 6, 6), and C (0, 7, 10) form a right-angled isosceles triangle.

Sol:

Distance between two points P (x₁, y₁, z₁) and Q (x₂, y₂, z₂) is PQ =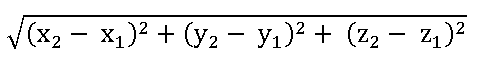

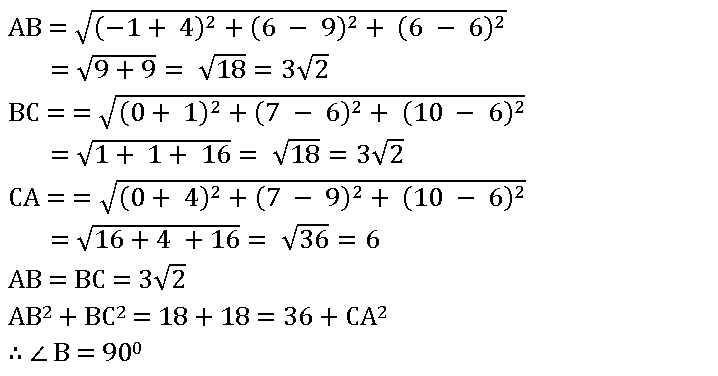
∴ The points A (– 4, 9, 6), B (– 1, 6, 6) and C (0, 7, 10) form a right-angled isosceles triangle.

2. Show that the locus of the point whose distance from Y – axis is thrice its distance from (1, 2, – 1) is 8x ² + 9y² + 8 z² – 18x – 36y + 18z + 54 = 0

Sol:

Let P (x, y, z) be the locus of the point

        A (0, y, 0) be any point on Y – axis

         B = (1, 2, – 1)

     Condition is PA = 3PB

                             PA² = (3PB)²

                             PA²= 9 PB² 

       ⟹ x² + z² = 9[(x – 1)² + (y – 2)² + (z + 1)²]

            x² + z² = 9[x² – 2x + 1 + y² – 4y + 4 + z² + 2z + 1]

           x² + z² = 9x² – 18x + 9 + 9y² – 36y + 36 +9 z² + 18z + 9

          ∴ 8x ² + 9y² + 8 z² – 18x – 36y + 18z + 54 = 0

3. A, B, and C are three points on OX, OY, and OZ respectively, at distances a, b, c (a≠0, b≠0, c≠0) from the origin ‘O’. Find the coordinate of the point which is equidistant from A, B, C, and O

Sol:

Let P (x, y, z) be the required point

    O = (0, 0, 0)   A = (a, 0, 0), B = (0, b, 0), C = (0, 0, c)

Given, AP = BP = CP = OP

             AP = OP

        ⟹   AP² =OP²

 (x – a )² + y² + z² = x² + y² + z²

  x² + a² – 2ax + y² + z² = x² + y² + z²

  a² – 2ax = 0

  a (a – 2x) = 0

    a – 2x = 0 (∵ a≠0)

    a = 2x ⟹ a/2

    Similarly, y = b/2 and z = c/2

∴ P = (a/2, b/2, c/2)

4. Show that the points A (3, – 2, 4), B (1, 1, 1) and C (– 1, 4, – 2) are collinear

Sol:

Given points are A (3, – 2, 4), B (1, 1, 1), and C (– 1, 4, – 2)

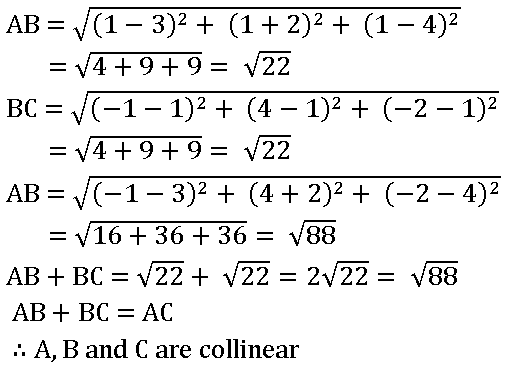
5.Find x if the distance between (5, – 1, 7), (x, 5, 1) is 9 units.

Sol:

 Let A = (5, – 1, 7), B = (x, 5, 1)

   Given AB = 9

    ⟹ AB² = 81

          (5 – x)² + (– 1 – 5)² + (7 – 1)² = 81

         (5 – x)² + 36 + 36 = 81

         (5 – x)² + 72 = 81

         (5 – x)² = 81 – 72 = 9

        (5 – x) = ± 3

     5 – x = 3 or 5 – x = – 3

    5 – 3 = x or 5 + 3 = x

     x = 2 or x = 8

6.If the point (1, 2, 3) is changed to point (2, 3, 1) through the translation of axes. Find a new origin.

Sol:

Given (x, y, z) = (1, 2, 3) and (X, Y, Z) = (2, 3, 1)

x = X + h, y = Y + k, z = Z + l

h = x – X, k = y – Y, l = z – Z

h = 1 – 2, k = 2 – 3, l = 3 – 1

h = – 1, k = – 1, l = 2

New origin is (– 1, – 1, 2)

7.By section formula, find the point which divides the line joining the points (2, – 3, 1) and (3, 4, – 5) in the ratio 1 : 3.

Sol:

If a point P divides the line segment joining the points (x₁, y₁, z₁), (x₂, y₂, z₂) in the ratio, then

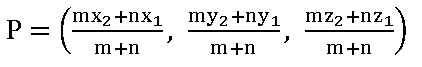
Let P divides the line joining the points (2, – 3, 1) and (3, 4, – 5) in the ratio 1 : 3

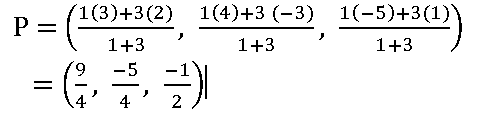
8.Find the ratio in which the line joining two points (7, 0, – 1) and (– 2, 3, 5) is divided by the point (1,2,3).

Sol:

Let A = (7, 0, – 1), B = (– 2, 3, 5) and P = (1,2,3)

Suppose P divides AB in the ratio k : 1

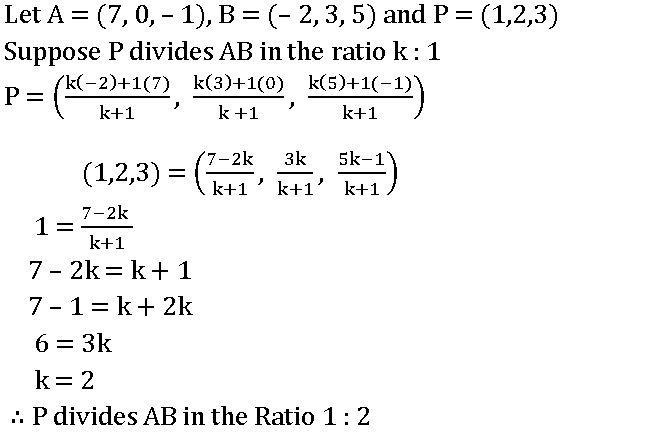
9.Using section formula, verify whether the points A (2, –4, 3), B (–4, 5, 6), C (4, –7, 2) are collinear or not.

Sol:

Given Points are A (2, –4, 3), B (–4, 5, 6), C (4, –7, 2)

Let C divides AB in the ratio k : 1

2 – 4k = 4 (k + 1)

 2 – 4k = 4k + 4

– 4k– 4k = 4 – 2

– 8k = 2

K = -1/4

C divides AB in the Ratio 1 : 4 externally

∴ A, B, C are collinear

10.Find the centroid of the triangle whose vertices are (5, 4, 6), (1, –1, 3) and (4, 3, 2)

Sol:

The centroid of the triangle whose vertices are (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) is

11. Find the centroid of the tetrahedron whose vertices are (2, 3, –4), (–3, 3, –2), (–1, 4, 2) and (3, 5, 1)

Sol:

The centroid of the tetrahedron whose vertices are (x₁, y₁, z₁), (x₂, y₂, z₂) (x₃, y₃, z₃), and (x₄, y₄, z₄) is 

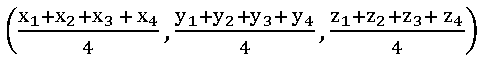
 the centroid of the tetrahedron whose vertices are (2, 3, –4), (–3, 3, –2), (–1, 4, 2) and (3, 5, 1) is

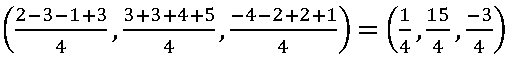
12. Find the ratio in which the YZ-plane divides the line joining A(2, 4, 5) and B (3, 5, – 4)

Sol:

Let P be any point on the YZ-plane

   P = (0, y, z)

 Let P divides AB int eh ratio k:1

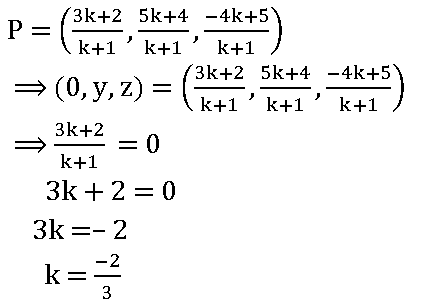
   YZ-plane divides AB in the ratio – 2:3

13. Find the fourth vertex of the parallelogram whose consecutive vertices are (2, 4, – 1), (3, 6, – 1) and (4, 5, 1).

Sol:  

let A = (2, 4, – 1), B = (3, 6, – 1), C = (4, 5, 1) and D = (x, y, z)

            ABCD is a parallelogram

            Midpoint of AC = Midpoint of BD

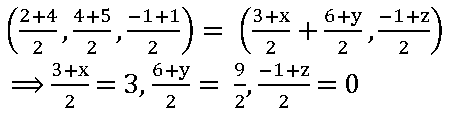
        ⟹ 3 + x = 6, 6 + y = 9, – 1 + z = 0

        x = 3, y = 3, z = 1

∴ The fourth vertex D = (3, 3, 1)

14. A (5, 4, 6), B (1, –1, 3), and C (3, 3, 1) are three points. Find the coordinates of the point at which the bisector of ∠BAC meets the side BC.

Sol:

We know that the bisector of ∠BAC divides BC in the ratio AB: AC

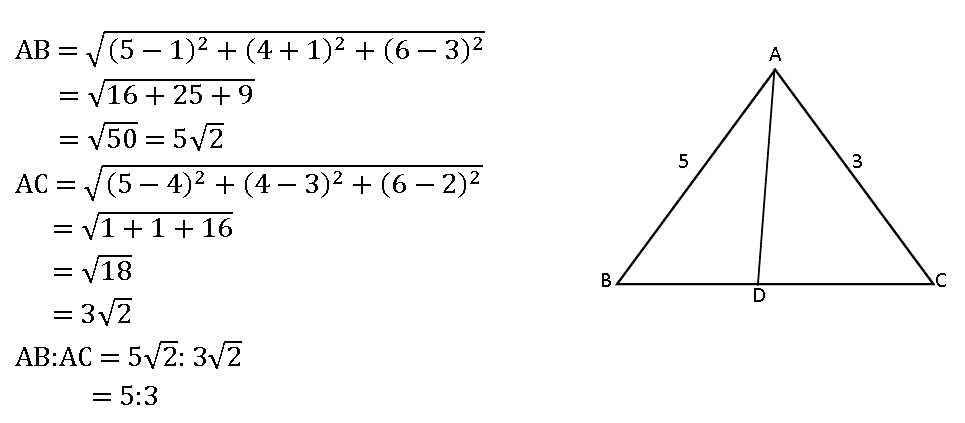
If D is a point where the bisector of ∠BAC meets BC

 ⟹ D divides BC in the ratio 5:3

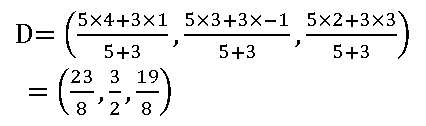
15. If M (α, β, γ) is the midpoint of the line joining the points (x₁, y₁, z₁) and B, then find B

Sol:

Let B (x, y, z) be the required point

 M is the midpoint of AB

⟹ (α, β, γ) =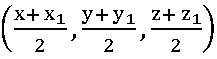

  ⟹ 2 α = x + x₁; 2 β = y + y₁; 2 γ = z + z₁

         x =2 α – x₁; x =2 β – y_1; x =2 γ – z₁

    ∴ B = (2 α – x₁, 2 β – y₁, 2 γ –)

16. If H, G, S, and I respectively denote the orthocenter, centroid, circumcenter, and incentre of a triangle formed by the points (1, 2, 3), (2, 3, 1) and (3, 1, 2), then find H, G, S, I.

Sol:

Let A = (1, 2, 3), B= (2, 3, 1), C = (3, 1, 2)

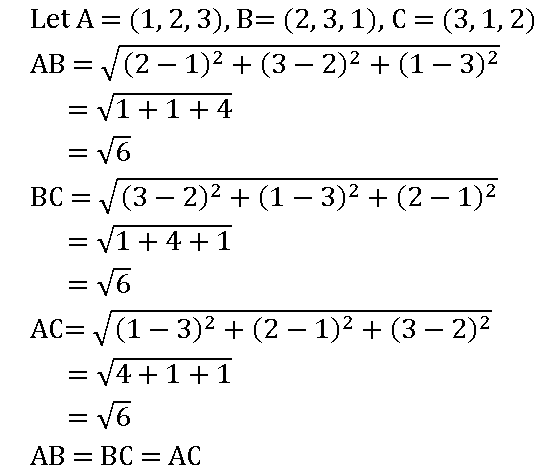
⟹ ∆ ABC is an equilateral triangle

 We know that, in an equilateral triangle orthocenter, centroid, circumcenter, and incentre are the same

Centroid G =

                      = (2, 2, 2)

∴ H = (2, 2, 2), S = (2, 2, 2), I = (2, 2, 2)

17. Find the incentre of the triangle formed by the points (0, 0, 0), (3, 0, 0) and (0, 4, 0).

Sol:

Let A = (0, 0, 0), B = (3, 0, 0) and C = (0, 4, 0)

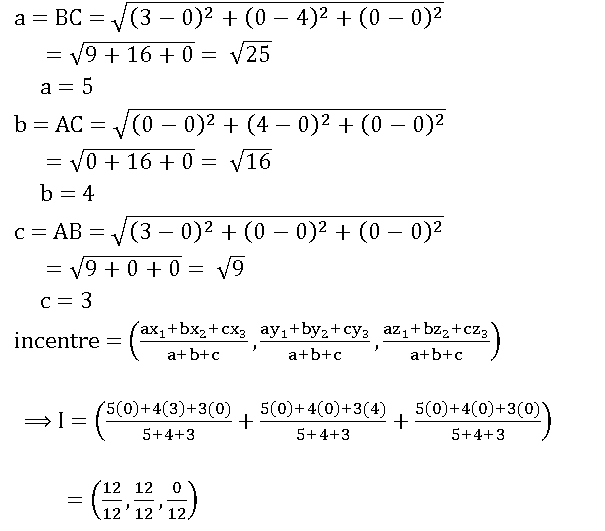
∴ I = (1, 1,0)

18. Find the ratio in which point P (5, 4, – 6) divides the line segment joining the points A (3, 2, – 4) and B (9, 8, –10). Also, find the harmonic conjugate of P

Sol:

Harmonic Conjugate: If P divides AB in the ratio m: n, then the Harmonic Conjugate of P (i.e., Q) divides AB in the ratio –m : n.

Given points are A (3, 2, – 4), B (9, 8, –10), and P (5, 4, – 6)

P divides AB in the ratio is x₂ – x : x – x₂

                                                     = 3 – 5 : 5 – 9

                                                      = 1 : 2 (internally)

Let Q be the harmonic conjugate of P

  ⟹ Q divides AB in the ratio –1 : 2

      Q =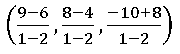

         = (–3, –4, –2)

Q (–3, –4, –2) is the hormonic conjugate of P (5, 4, – 6)

19. If (3, 2, – 1), (4, 1,1), and (6, 2, 5) are three vertices and (4, 2, 2) is the centroid of the tetrahedron, find the fourth Vertex.

Sol:

Given vertices of Tetrahedron are A (3, 2, – 1), B (4, 1,1), C (6, 2, 5) and centroid G = (4, 2, 2)

Let the fourth vertex is D = (x, y, z)

 The centroid of the tetrahedron whose vertices are (x₁, y₁, z₁), (x₂, y₂, z₂) (x₃, y₃, z₃), and (x₄, y₄, z₄) is

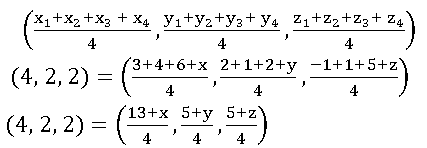
13 + x = 16, 5 + y = 8, 5 + z = 2

x = 3, y = 3, z = 3

∴ the fourth vertex D = (3, 3, 3)  

20. Show that the points A(3, 2, –4), (5, 4, –6), and C(9, 8, –10) are collinear and find the ratio in which B divides AC.

Sol:

Given points are A(3, 2, –4), (5, 4, –6) and C(9, 8, –10)

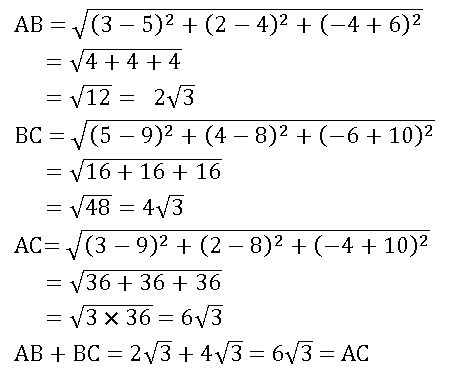
∴ points A (3, 2, –4), (5, 4, –6), and C (9, 8, –10) are collinear

      B divides AB in the ratio is AB: BC = 

Visit my Youtube Channel: Click on Below Logo